Использование операторов polyfit и polyval для аппроксимации кривой
Цель работы.
Получение полинома, описывающего аппроксимированную кривую наиболее близкую к исходной, которая построена по точкам.
Исходные данные.
| x | 0 | 400 | 800 | 1200 | 1600 | 2000 | 2400 | 2800 | 3200 |
| f(x) | 0 | 80 | 100 | 110 | 120 | 180 | 210 | 230 | 260 |
Программа.
%Исходные данные
x=[0 400 800 1200 1600 2000 2400 2800 3200];
f=[0 80 100 110 120 180 210 230 260];
%a - коэффициенты полинома
%S - квадратичная погрешность
[a,S]=polyfit(x,f,3)
z=polyval(a,x)
%Построение графиков
plot(x,f,x,z),grid
Результат.
a =
0.0000 -0.0000 0.1223 13.5354
S =
R: [4x4 double]
df: 5
normr: 43.1607
z =
Columns 1 through 7
13.5354 57.1717 91.9986 120.6926 145.9307 170.3896 196.7460
Columns 8 through 9
227.6768 265.8586
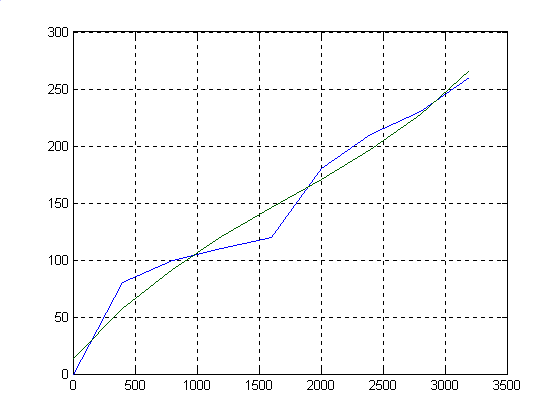
Командой plot произвели построение исходной функции (синий цвет) и функции аппроксимирующей её (зелёный цвет). Поскольку велико значение погрешности normr=43.1607 и недостаточно аппроксимирование, то следует повысить степень полинома. Пусть вместо 3 будет 6.
Программа.
%Исходные данные
x=[0 400 800 1200 1600 2000 2400 2800 3200];
f=[0 80 100 110 120 180 210 230 260];
%a - коэффициенты полинома
%S - квадратичная погрешность
[a,S]=polyfit(x,f,6)
z=polyval(a,x)
%Построение графиков
plot(x,f,x,z),grid
Результат.
a =
0.0000 -0.0000 0.0000 -0.0000 -0.0002 0.2770 0.0140
S =
R: [7x7 double]
df: 2
normr: 12.4672
z =
Columns 1 through 7
0.0140 79.7016 101.6970 105.3007 127.5058 172.6900 214.3077
Columns 8 through 9
228.5828 260.2005
Вывод.
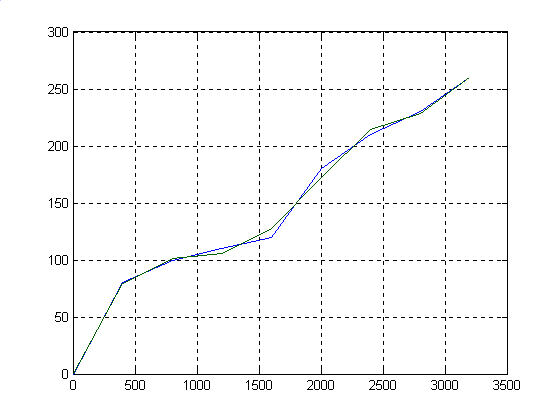
В результате работы видно, что при увеличении степени полинома уменьшается погрешность и аппроксимированная кривая наиболее близка к исходной. В случае когда степень полинома равна количеству исходных точек, получаем: normr=0 и полное соответствие кривых в исходных точках.
Оптимальное распределение двух ресурсов
Цель работы.
Получение максимального значения прибыли при перевозке двух различных грузов.
Исходные данные.
| x | 0 | 400 | 800 | 1200 | 1600 | 2000 | 2400 | 2800 | 3200 |
| f1(x) | 0 | 80 | 100 | 110 | 120 | 180 | 210 | 230 | 260 |
| f2(x) | 0 | 60 | 90 | 110 | 130 | 150 | 190 | 230 | 250 |
f1(x) доход от перевозки груза первого рода;
f2(x) доход от перевозки груза второго рода;
x количество груза.
Программа.
%Исходные данные
x=[0 400 800 1200 1600 2000 2400 2800 3200];
f1=[0 80 100 110 120 180 210 230 260];
f2=[0 60 90 110 130 150 190 230 250];
plot(x,f1,x,f2),grid
%Решение
F12=[];
for xR=1:9;
I=1:xR;
L12=f1(I)+f2(xR-I+1);
[Lopt,I]=max(L12);
x1=I*400-400;
x2=(xR-I)*400;
Pacn=[Lopt;x1;x2;x1+x2];
F12=[F12 Pacn];
end
F12
pause
plot(x,F12(1,:)),grid
Результат.
F12 =
Columns 1 through 6
0 80 140 170 190 210
0 400 400 400 400 400
0 0 400 800 1200 1600
0 400 800 1200 1600 2000
Columns 7 through 9
240 270 310
2000 400 400
400 2400 2800
2400 2800 3200
В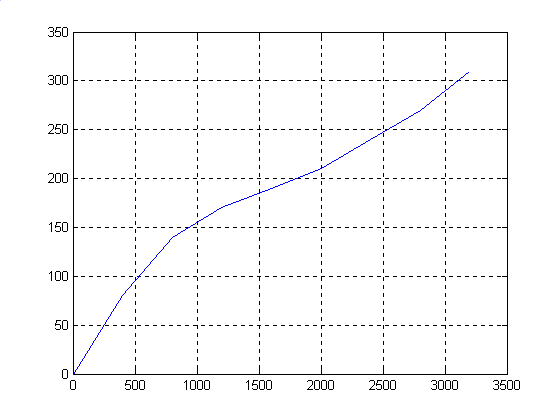 результате
получаем матрицу,
в которой:
результате
получаем матрицу,
в которой:
1 строка суммарный доход от перевозки;
2 строка количество первого груза;
3 строка количество второго груза;
4 строка суммарное количество грузов.
Вывод.
Таким образом получена оптимальная зависимость распределения груза с наибольшим доходом от перевозки. Для наглядности по полученным значениям построен график.
Оптимальное распределение шести ресурсов
Цель работы.
Получение максимального значения прибыли при перевозке шести различных грузов.
Исходные данные.
| x | 0 | 400 | 800 | 1200 | 1600 | 2000 | 2400 | 2800 | 3200 |
| f1(x) | 0 | 80 | 100 | 110 | 120 | 180 | 210 | 230 | 260 |
| f2(x) | 0 | 60 | 90 | 110 | 130 | 150 | 190 | 230 | 250 |
| f3(x) | 0 | 30 | 40 | 70 | 110 | 180 | 200 | 240 | 250 |
| f4(x) | 0 | 40 | 60 | 80 | 130 | 160 | 180 | 210 | 240 |
| f5(x) | 0 | 50 | 70 | 90 | 110 | 150 | 170 | 200 | 220 |
| f6(x) | 0 | 70 | 80 | 110 | 140 | 160 | 200 | 250 | 270 |
f1(x) доход от перевозки груза первого рода;
f2(x) доход от перевозки груза второго рода;
f3(x) доход от перевозки груза третьего рода;
f4(x) доход от перевозки груза четвёртого рода;
f5(x) доход от перевозки груза пятого рода;
f6(x) доход от перевозки груза шестого рода;
x количество груза.
Программа.
%Исходные данные
x=[0 400 800 1200 1600 2000 2400 2800 3200];
f1=[0 80 100 110 120 180 210 230 260];
f2=[0 60 90 110 130 150 190 230 250];
f3=[0 30 40 70 110 180 200 240 250];
f4=[0 40 60 80 130 160 180 210 240];
f5=[0 50 70 90 110 150 170 200 220];
f6=[0 70 80 110 140 160 200 250 270];
F=[f1;f2;f3;f4;f5;f6];
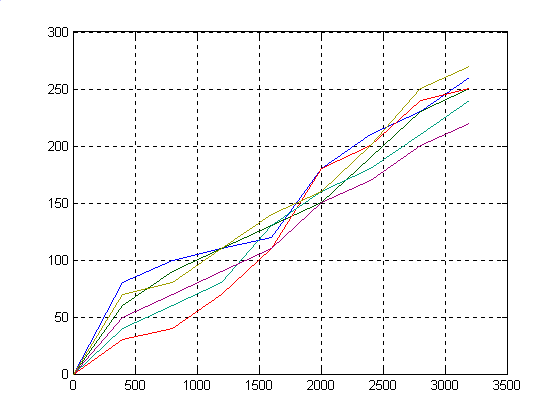
plot(x,F),grid
%Решение
FF=[];
J=1;
for XR=1:9;
I=1:XR;
L=F(J,I)+F(J+1,XR-I+1);
[Lopt,I]=max(L);
x1=I*400-400;
x2=(XR-I)*400;
Pacn=[Lopt;x1;x2;x1+x2];
FF=[FF Pacn];
end
D=FF(1,:);
PP=[];
RRR=[];
for J=2:5;
DD=[];
RR=[];
for XR=1:9;
I=1:XR;
L=D(I)+F(J+1,XR-I+1);
[Lopt,I]=max(L);
x1=I*400-400;
x2=(XR-I)*400;
Pacn=[Lopt;x1;x2;x1+x2];
DD=[DD Pacn(1,:)];
 RR=[RR Pacn];
RR=[RR Pacn];
end
PP=[PP;DD(1,:)];
RRR=[RRR RR];
D=DD;
end
RRR=[FF RRR]
pause
plot(x,RRR(1,37:45)),grid
Результат.
RRR =Columns 1 through 6
0 80 140 170 190 210
0 400 400 400 400 400
0 0 400 800 1200 1600
0 400 800 1200 1600 2000
Columns 7 through 12
240 270 310 0 80 140
2000 400 400 0 400 800
400 2400 2800 0 0 0
2400 2800 3200 0 400 800
Columns 13 through 18
170 200 220 260 320 350
800 1200 1600 400 800 1200
400 400 400 2000 2000 2000
1200 1600 2000 2400 2800 3200
Columns 19 through 24
0 80 140 180 210 240
0 400 800 800 1200 1600
0 0 0 400 400 400
0 400 800 1200 1600 2000
Columns 25 through 30
270 320 360 0 80 140
800 2800 2800 0 400 800
1600 0 400 0 0 0
2400 2800 3200 0 400 800
Columns 31 through 36
190 230 260 290 320 370
800 1200 1600 2000 2400 2800
400 400 400 400 400 400
1200 1600 2000 2400 2800 3200
Columns 37 through 42
0 80 150 210 260 300
0 400 400 800 1200 1600
0 0 400 400 400 400
0 400 800 1200 1600 2000
Columns 43 through 45
330 360 390
2000 2400 2800
400 400 400
2400 2800 3200
В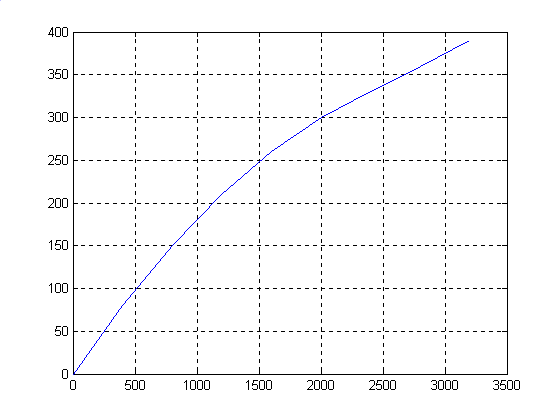 результате
получаем матрицу,
в которой:
результате
получаем матрицу,
в которой:
1 строка доход от перевозки i грузов;
2 строка ![]() количества грузов;
количества грузов;
3 строка количество i-ого груза;
4 строка суммарное количество грузов.
Вывод.
Таким образом получена оптимальная зависимость распределения груза с наибольшим доходом от перевозки. Для наглядности по полученным значениям построен график.
Оптимизация режима движения судна
Цель работы.
Распределить скорость движения судна по четырём участкам трассы так, чтобы суммарный расход топлива был минимальным.
Программа.
%Подготовка исходных данных
delt=0.07;
tmin=[5.86 2.73 1.6 3.3967]; tmax=[7.47 3.71 2.37 4.5167];
t=[tmin; tmax]; tb=[tmax-tmin];
G1=[967.42 941.39 912 892.29 878.02 846.11 823.73 798.51 775.22 ...
764.2 741.28 719.36 706.85 678.15 673.74 659.91 645.65 ...
630.98 623 610.9 598.95 590.07 577.2 571.46];
G2=[521.73 491.12 463.51 437.33 415.2 392.7 377.45 358.23 346.86 ...
328.98 316.25 305.38 295.48 285.86 277.11];
G3=[281.47 255.5 231.07 210.41 192.31 177.55 166.97 157.77 ...
149.86 144.48 140.91 139.23];
G4=[590.60 561.90 535.10 510.20 487.06 465.67 445.94 427.82 ...
411.23 396.12 382.42 370.06 358.99 349.13 340.42 332.80 325.41];
%Формирование векторов t1, t2, t3, t4
t1=t(1,1):delt:t(2,1);
t2=t(1,2):delt:t(2,2);
t3=t(1,3):delt:t(2,3);
t4=t(1,4):delt:t(2,4);
%Пригонка данных
[a1,H1]=polyfit(t1,G1,3);
[a2,H2]=polyfit(t2,G2,3);
[a3,H3]=polyfit(t3,G3,3);
[a4,H4]=polyfit(t4,G4,3);
a=[a1;a2;a3;a4];
%Апроксимация исходных зависимостей
N=25;
deltM=tb./(N-1);
%Моделирование
TM=[];Gm=[];
for i=1:4;
tm=t(1,i):deltM(i):t(2,i);
TM=[TM;tm];
gm=polyval(a(i,:),tm);
Gm=[Gm;gm];
end
deltt=deltM;
%Оптимизация распределения времени движения
GG=[];
F=Gm;
for xr=1:N;
I=1:xr;
L=Gm(1,I)+Gm(2,xr-I+1);
[Lopt,I]=min(L);
X1=5.86+I*deltt(1)-deltt(1);
X2=2.73+(xr-I)*deltt(2);
Pacn=[Lopt.*0.001;X1;X2;X1+X2];
GG=[GG Pacn];
end
D=GG(1,:);
C=GG(4,:);
PP=[];RRR=[];
for J=2:3;
DD=[];RR=[];CC=[];
for xr=1:N;
I=1:xr;
L=D(I)+0.001.*F(J+1,xr-I+1);
[Lopt,I]=min(L);
X1=C(I);
X2=TM(J+1,1)+(xr-I)*deltt(J+1);
Pacn=[Lopt;X1;X2;X1+X2];
DD=[DD Pacn(1,:)];
RR=[RR Pacn];
CC=[CC Pacn(4,:)];
end
PP=[PP;DD(1,:)];
RRR=[RRR RR];
D=DD;
C=CC;
end
RRR=[GG RRR];
R12=RRR(:,1:N)
R23=RRR(:,N+1:2*N)
R34=RRR(:,2*N+1:3*N)
plot(R34(1,:),R34(4,:)),grid
Результат.
R12 =
Columns 1 through 7
1.4899 1.4647 1.4402 1.4164 1.3934 1.3710 1.3494
5.8600 5.9271 5.9942 6.0613 6.1283 6.1954 6.2625
2.7300 2.7300 2.7300 2.7300 2.7300 2.7300 2.7300
8.5900 8.6571 8.7242 8.7912 8.8583 8.9254 8.9925
Columns 8 through 14
1.3285 1.3083 1.2889 1.2703 1.2522 1.2343 1.2172
6.3296 6.3967 6.4638 6.5308 6.5308 6.5979 6.5979
2.7300 2.7300 2.7300 2.7300 2.7708 2.7708 2.8117
9.0596 9.1267 9.1937 9.2608 9.3017 9.3688 9.4096
Columns 15 through 21
1.2001 1.1838 1.1675 1.1521 1.1367 1.1220 1.1075
6.6650 6.7321 6.7321 6.7992 6.7992 6.8663 6.8663
2.8117 2.8117 2.8525 2.8525 2.8933 2.8933 2.9342
9.4767 9.5437 9.5846 9.6517 9.6925 9.7596 9.8004
Columns 22 through 25
1.0936 1.0799 1.0668 1.0538
6.9333 6.9333 7.0004 7.0004
2.9342 2.9750 2.9750 3.0158
9.8675 9.9083 9.9754 10.0162
R23 =
Columns 1 through 7
1.7720 1.7468 1.7223 1.6985 1.6754 1.6530 1.6314
8.5900 8.6571 8.7242 8.7912 8.8583 8.9254 8.9925
1.6000 1.6000 1.6000 1.6000 1.6000 1.6000 1.6000
10.1900 10.2571 10.3242 10.3912 10.4583 10.5254 10.5925
Columns 8 through 14
1.6105 1.5904 1.5710 1.5523 1.5342 1.5164 1.4992
9.0596 9.1267 9.1937 9.2608 9.3017 9.3688 9.4096
1.6000 1.6000 1.6000 1.6000 1.6000 1.6000 1.6000
10.6596 10.7267 10.7937 10.8608 10.9017 10.9688 11.0096
Columns 15 through 21
1.4821 1.4658 1.4496 1.4341 1.4187 1.4040 1.3895
9.4767 9.5437 9.5846 9.6517 9.6925 9.7596 9.8004
1.6000 1.6000 1.6000 1.6000 1.6000 1.6000 1.6000
11.0767 11.1437 11.1846 11.2517 11.2925 11.3596 11.4004
Columns 22 through 25
1.3756 1.3619 1.3488 1.3358
9.8675 9.9083 9.9754 9.9754
1.6000 1.6000 1.6000 1.6321
11.4675 11.5083 11.5754 11.6075
R34 =
Columns 1 through 7
2.3626 2.3374 2.3129 2.2892 2.2661 2.2437 2.2221
10.1900 10.2571 10.3242 10.3912 10.4583 10.5254 10.5925
3.3967 3.3967 3.3967 3.3967 3.3967 3.3967 3.3967
13.5867 13.6538 13.7209 13.7879 13.8550 13.9221 13.9892
Columns 8 through 14
2.2012 2.1810 2.1616 2.1422 2.1236 2.1051 2.0870
10.6596 10.7267 10.7267 10.7937 10.8608 10.8608 10.9017
3.3967 3.3967 3.4434 3.4434 3.4434 3.4900 3.4900
14.0563 14.1234 14.1700 14.2371 14.3042 14.3509 14.3917
Columns 15 through 21
2.0691 2.0514 2.0343 2.0172 2.0004 1.9841 1.9678
10.9688 10.9688 11.0096 11.0767 11.0767 11.1437 11.1846
3.4900 3.5367 3.5367 3.5367 3.5834 3.5834 3.5834
14.4588 14.5055 14.5463 14.6134 14.6600 14.7271 14.7679
Columns 22 through 25
1.9518 1.9363 1.9209 1.9057
11.1846 11.2517 11.2925 11.2925
3.6300 3.6300 3.6300 3.6767
14.8146 14.8817 14.9225 14.9692
В результате получаем матрицы, в которых:
1 строка расход топлива на участках;
2 строка время движения по предыдущим участкам;
3 строка время движения по i-тому участку;
4 строка суммарное время движения по участкам.
R12 результаты для двух участков;
R23 результаты для трёх участков;
R34 результаты для четырёх участков;
Вывод.
 В
качестве вывода
приведена
графическая
зависимость
расхода топлива
(ось абсцисс)
от времени
прохождения
всех участков
(ось ординат).
В
качестве вывода
приведена
графическая
зависимость
расхода топлива
(ось абсцисс)
от времени
прохождения
всех участков
(ось ординат).
Оптимальные режимы работы судовых генераторных агрегатов
Цель работы.
Найти оптимальное распределение мощности между дизель-генераторами.
Программа.
%Исходные данные
delt=10;
P1=0:delt:50;
P2=0:delt:70;
P3=0:delt:80;
F1=(0.03*(P1.^2)+2*P1+80);
F2=(0.015*(P2.^2)+1.45*P2+100);
F3=(0.01*(P3.^2)+0.95*P3+120);
%Решение
for T=1:2;
r1=size(F1);
r2=size(F2);
if r1(2)
Похожие работы
... датчика, наличием нерассматриваемых источников тепла, особенностями конфигурации компонентов относительно потока воздуха от вентиляторов и др.). Это еще раз доказывает актуальность проведения экспериментальных исследований в изучении тепловых режимов устройств ЭВМ и, следовательно, создание для этих целей специализированного устройства (модуля). 7 РАЗРАБОТКА ТЕХНОЛОГИИ СБОРКИ МОДУЛЯ АЦП 7.1 ...
... —230 °С до влажности 2—5%. Готовые изделия имеют предел прочности при изгибе не менее 0,3 МПа, среднюю плотность не более 200 кг/м3, водопоглощение не выше 70% по массе и теплопроводность 0,051 Вт/(м • °С). Глава 4. ОЧИСТКА СТОЧНЫХ ВОД ЦЕЛЛЮЛОЗНО-БУМАЖНОГО ПРОИЗВОДСТВА МЕТОДОМ КОМПЛЕКСООБРАЗОВАНИЯ Проблема влияния целлюлозно-бумажного производства (ЦБП) на состояние водных экосистем носит ...
... при температуре 25 град.С, атмосферном давлении 80-106 кПА (от 630 до 800 мм рт.ст.) и может входить в состав оборудования для автоматизации (телемеханизации) водоподъёмных станций (организация диспетчеризации и централизованного управления несколькими удалёнными системами). 2. При разработке автоматизированной системы управления водозабором были предусмотрены следующие контролируемые параметры: ...
... своевременное распределение средств на развитие. Данными вопросами я и занимаюсь в настоящей дипломной работе. 4. Математическое моделирование Интернет - услуг 4.1 Математическое моделирование dial-up подключений Сначала рассмотрим моделирование услуги предоставления доступа в Интернет по dial-up, так как данная услуга является показателем потенциальных абонентов для монопольной услуги ...
0 комментариев