МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ.
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННО-ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
им. К.Э. ЦИОЛКОВКОГО
КАФЕДРА ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовой работе на тему: “Разработка алгоритмов и
программ выполнения операций над последовательными
и связанными представлениями структур данных”
по курсу “Теория алгоритмов и вычислительных
методы”
Руководитель: Авдошин С.М.
Дата сдачи: _____________
Подпись: _____________Студент: Лицентов Д.Б.
Группа: 3ИТ-2-26
Москва
1998
1. Постановка задачи.
Дано:
Два орграфа X и Y с N вершинами (X в последовательном представлении, Y в связанном представлении) без кратностей. Дуги орграфов образуют неупорядоченные списки. Орграфы задаются неупорядоченными списками смежных вершин - номеров вершин, в которые ведут ребра из каждой вершины графа.
Требуется:
Выполнить над ребрами орграфов операцию разности(X/Y). В результате выполнения этой операции новый орграф Z определяется в связанном представлении, а старый орграф X исправляется в последовательном представлении.
Особенности представления данных:
Последовательное представление данных: одномерный массив Array, содержащую два целочисленных поля I (содержит номер вершины, из которой исходит дуга) и J (содержит номер вершины, в которую входит дуга).
| Array[_] | I | J | |||
| | From | To | |||
| Array[ 2 ] | From | To | |||
| … | From | To | |||
| Array[ N ] | From | To | |||
N – количество дуг в орграфе X.
Связанное представление данных: одномерный массив Spisok указателей на структуру index, представляющую собой элемент списка и содержащий поле: целочисленное index (содержит номер вершины, в которую входит дуга) и Next - указатель на структуру Spisok, указывающее на следующий элемент списка
| Spisok[ _ ] | NEXT | index | next | index | next | Index | Next | |||
| | To | … | To | NULL | ||||||
| … | To | … | To | NULL | ||||||
| Spisok[ N ] | To | … | To | NULL |
N - количество вершин в графе Y,Z.
2. Внешнее описание программы.
Ввод информации об неориентированных графах происходит из файла, формат которого должен быть нижеследующим:
N
X11 X12 ... X1k1 0
X21 X22 ... X2k2 0
...
XN1 XN2 ... XNkN 0
Y11 Y12 ... Y1k1 0
Y21 Y22 ... Y2k2 0
...
YN1 YN2 ... YNkN 0
где N - число вершин в графах
Xij - номер очередной вершины смежной i в графе X (i = 1..N, j=1..ki)
Yij - номер очередной вершины смежной i в графе Y(i = 1..N, j=1..ki)
Если из какой-то вершины не выходит ни одного ребра, то для нее в исходных данных задаем только ноль (например ‘0’ - вершина 2 изолирована). Таким образом, для каждого графа должно вводится в общей сложности N нолей.
Формат печати результатов работы программы представлен в следующем формате:
Даны неориентированные графы X и Y без кратностей.
Для каждого графа задаем номера вершины смежности с данной.
Граф X (в ЭВМ в последовательном представлении):
1 : X11 X12 ... X1k1
2 : X21 X22 ... X2k2
...
N : XN1 XN2 ... XNkN
Граф Y (в ЭВМ в связанном представлении):
1 : Y11 Y12 ... Y1k1
2 : Y21 Y22 ... Y2k2
...
N : YN1 YN2 ... YNkN
Над графами выполняется операция разности двумя способами
с получением нового графа Z (в связанном представлении):
1 : Z11 1,Z12 ... Z1k1
2 : Z21 Z22 ... Z2k2
...
N : ZN1 ZN2 ... ZNkN
И исправлением старого графа X (в последовательном представлении):
1 : X11 X12 ... X1k1
2 : X21 X22 ... X2k2
...
N : XN1 XN2 ... XNkN
Кол-во вершин, кол-во дуг графа X, кол-во дуг графа Y
и кол-во времени, затраченного на вычисление разности X и Y:
N MX MY T
где T - кол-во времени, затраченного на вычисление разности X и Y
Zij - номер очередной вершины смежной i в графе Z(i = 1..N, j=1..ki)
MX - кол-во дуг в графе X
MY - кол-во дуг в графе Y
Метод решения:
Принцип решения основан на методе полного перебора, что конечно не лучший вариант, но все-таки лучше, чем ничего.
Аномалии исходных данных и реакция программы на них:
нехватка памяти при распределение: вывод сообщения на экран и завершение работы программы;
неверный формат файла: вывод сообщения на экран и завершение работы программы;
Входные данные
Входными данными для моей работы является начальное число вершин графа, которое по мере работы программы увеличиться на 30 верши. Это число не может превосходить значения 80 вершин, так как в процессе работы программы число увеличивается на 30 и становиться 110 – это «критическое» число получается из расчета 110216/3. Это происходит потому, что стандартный тип int не может вместить в себя более чем 216. Мне же требуется для нормально работы программы, чтобы тип вмещал в себя утроенное количество вершин неориентированного графа. Конечно, это всего лишь приближение, но с учётом того, что графы генерируются случайно возможность набора 33000 невелико и, следовательно, допустимо.
Входной файл генерируется каждый раз новый.
Графы для расчета мультипликативных констант генерируются случайным образом, используя датчик случайных чисел, это-то и накладывает ограничения на количество вершин. Дело в том, что при работе с генератором случайных чисел предпостительно иоспользовать целый тип данных – так говорил товарищ Подбельский В.В.
Оценка временной сложности.
Каткие сведения о временной сложности.
Качество алгоритма оценивается как точность решения и эффективность алгоритма, которая определяется тем временем, которое затрачивается для решения задачи и необходимым объёмом памяти машины.
Временная
сложность
алгоритма есть
зависимость
от количества
выполняемых
элементарных
операций как
функция размерности
задачи. Временная
сложность
алгоритма А
обозначается
![]() .
.
Размерность задачи – это совокупность параметров, определяющих меру исходных данных. Временная оценка алгоритма бывает двух типов:
априорная – асимптотическая оценка сложности ![]()
апосториорная – оценка сложности алгоритма с точностью до мультипликативных констант, сделанных для конкретной машины.
Именно
асимптотическая
оценка алгоритма
определяет
в итоге размерность задачи, которую
можно решить
с помощью ЭВМ.
Если алгоритм
обрабатывает
входные данные
размера N
за время
CN2,
где С
– некая постоянная,
то говорят, что
временная
сложность этого
алгоритма есть
![]() .
Вернее говорить,
что положительная
и нулевая функция
.
Вернее говорить,
что положительная
и нулевая функция ![]() есть
есть ![]() ,
если существует
такая постоянная
С,
что
,
если существует
такая постоянная
С,
что ![]() для всех отрицательных
значений N.
для всех отрицательных
значений N.
Вычисление временной сложности.
Для того, чтобы проверить правильность временной оценки алгоритма, надо знать априорную оценку сложности.
Проверка вычислительной сложности алгоритма сводиться к экспериментальному сравнению двух или более алгоритмов, решающих одну и ту же задачу. При этом возникают две главные проблемы: выбор входных данных и перевода результатов эксперимента в графики кривых сложности.
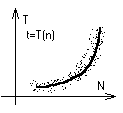
При прогоне программы мы получаем значения функции, которые можно изобразить на графике как функцию f(NX,NY,NZ). Данные точки показывают характер кривой. Для аппроксимации этого облака точек в своей курсовой работе я использовал метод наименьших квадратов.
Анализ по методу наименьших квадратов заключается в определении параметров кривой, описывающих связь между некоторым числом N пар значений Xi, Yi (в данном случае n и t соответственно), обеспечивая при этом наименьшую среднеквадратичную погрешность. Графически эту задачу можно представить следующим образом – в облаке точек Xi, Yi плоскости XY (смотри рисунок) требуется провести прямую так, чтобы величина всех отклонений отвечала условию:
N
F =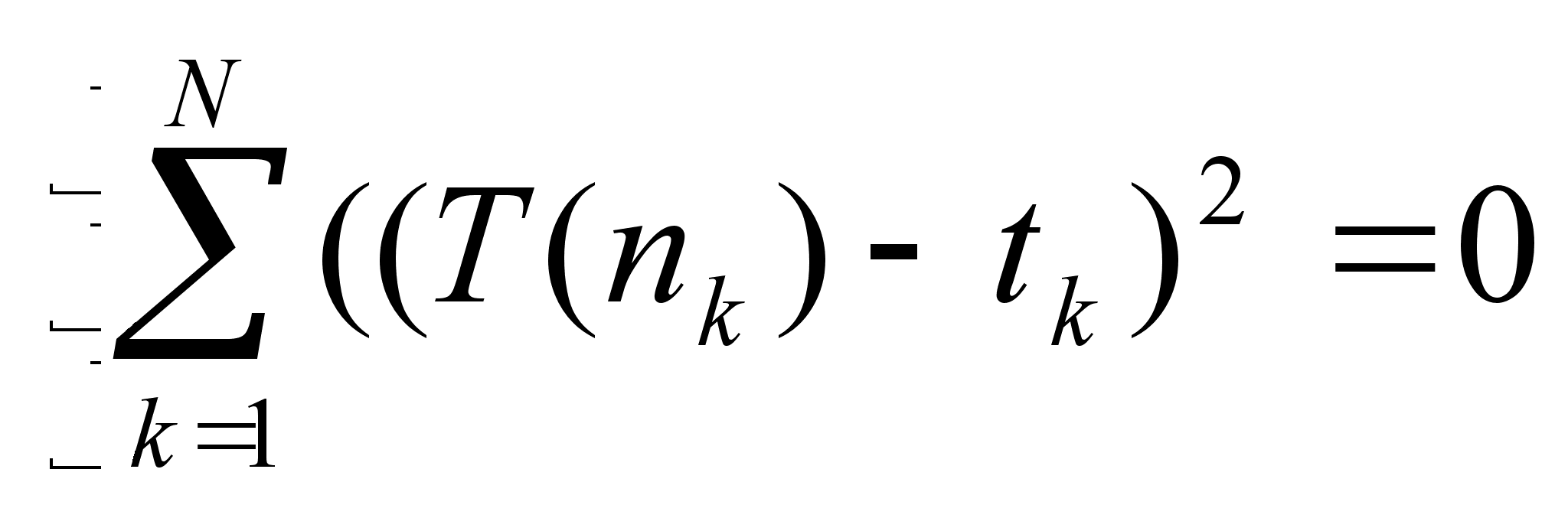
K=1
Где
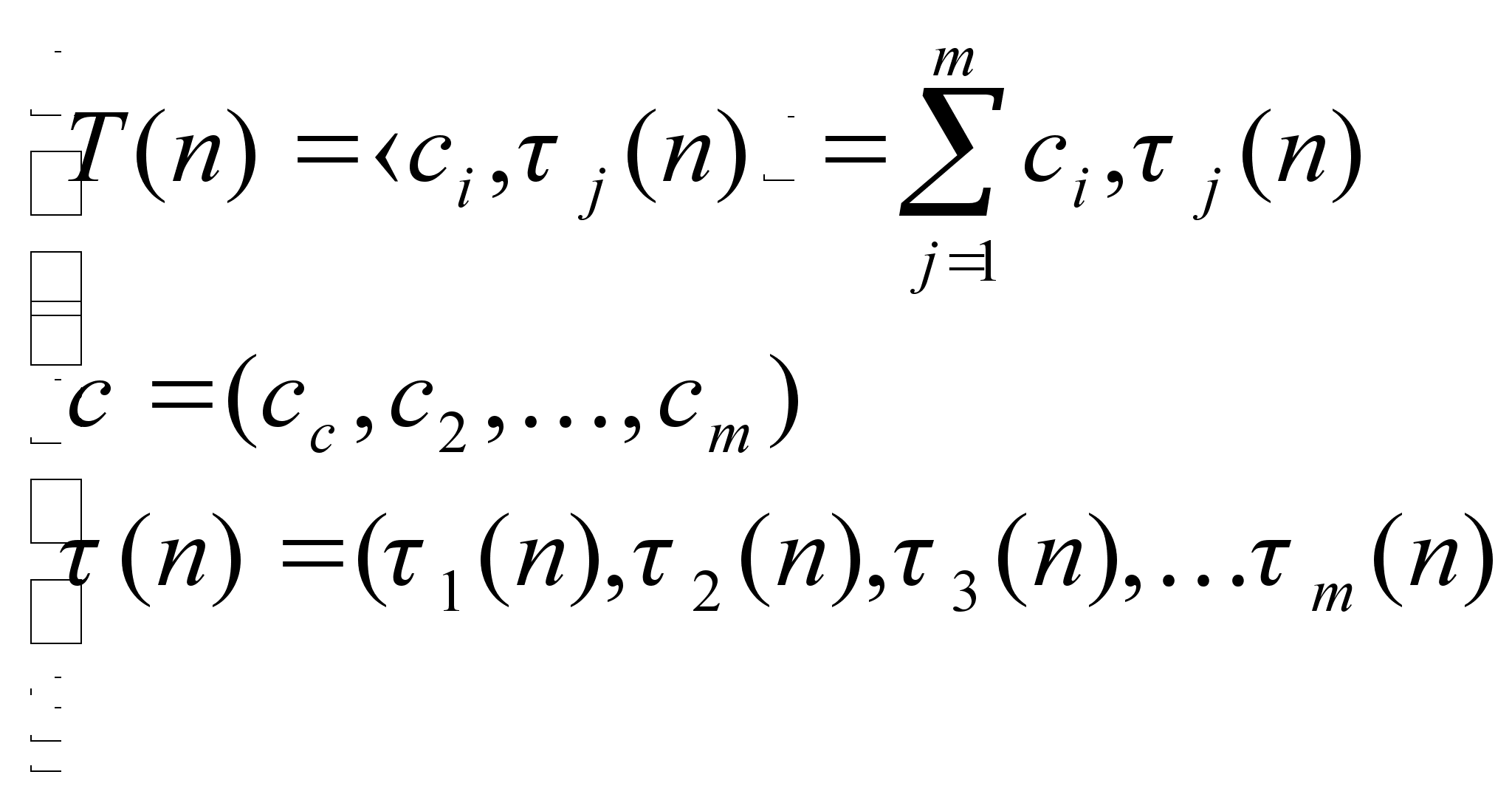
В моём случае T(NX,NY,NZ)=O(NX*(NY+NZ) =>
T(NX,NY,NZ)=C1*NX*(NY+NZ)+C2*(NY+NZ)+C3*(NY)+C4*(NZ)
Следовательно для моего примера мы получим:
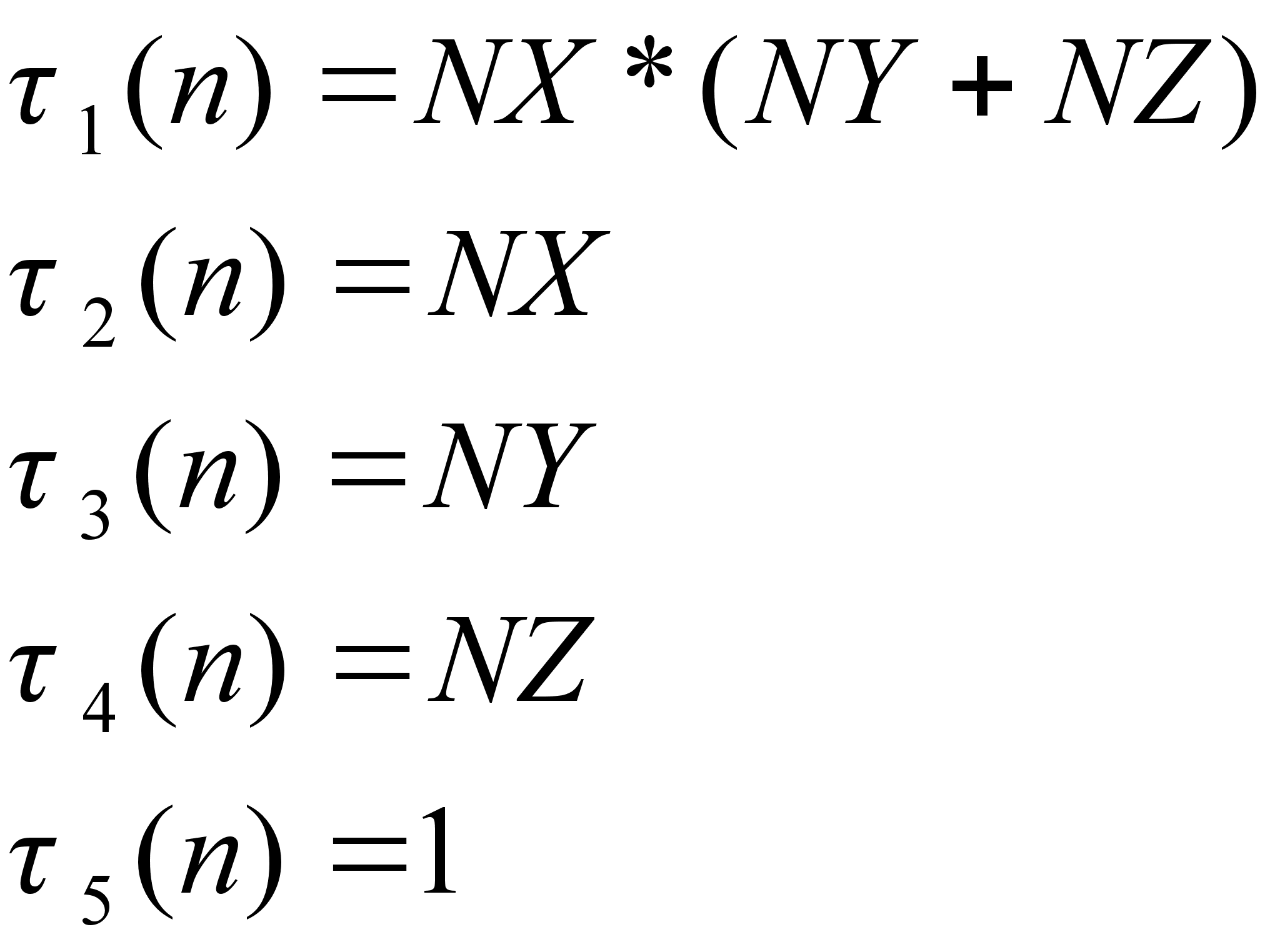
Для того чтобы получить значение функции на K-том эксперименте, мы засекаем значение времени перед вызовом функции, которая реализует алгоритм, вставим оператор вида:
TikTak=clock();
Где функция clock() даёт время с точностью до нескольких миллисекунд (в языке С++ она описана в заголовочном файле time.h). После выполнения процедуры, реализует алгоритм, мы находим разность времени
TikTak=cloc() - TikTak;
После всех проделанных манипуляций нужно прировнять к нулю все частные производные. Это будет выглядеть, в общем виде, примерно так:
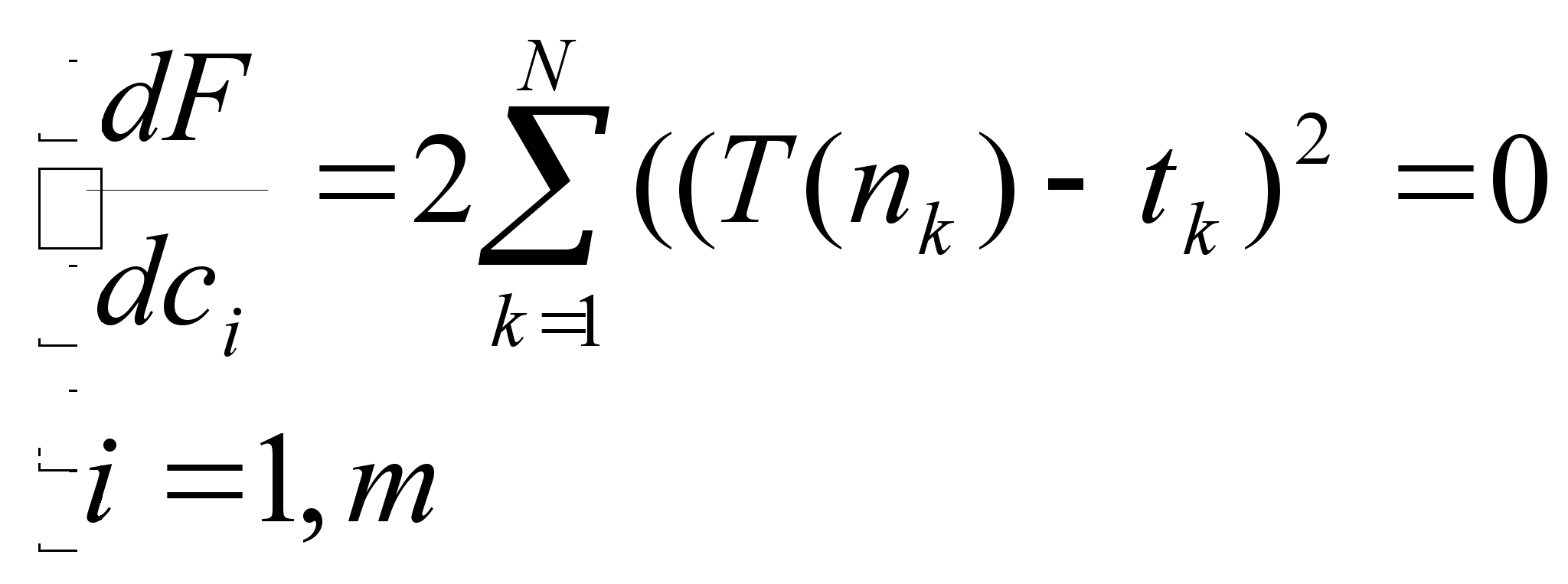
После раскрытия
скобок и замены
T(n)= T(n)=(c,(n))=
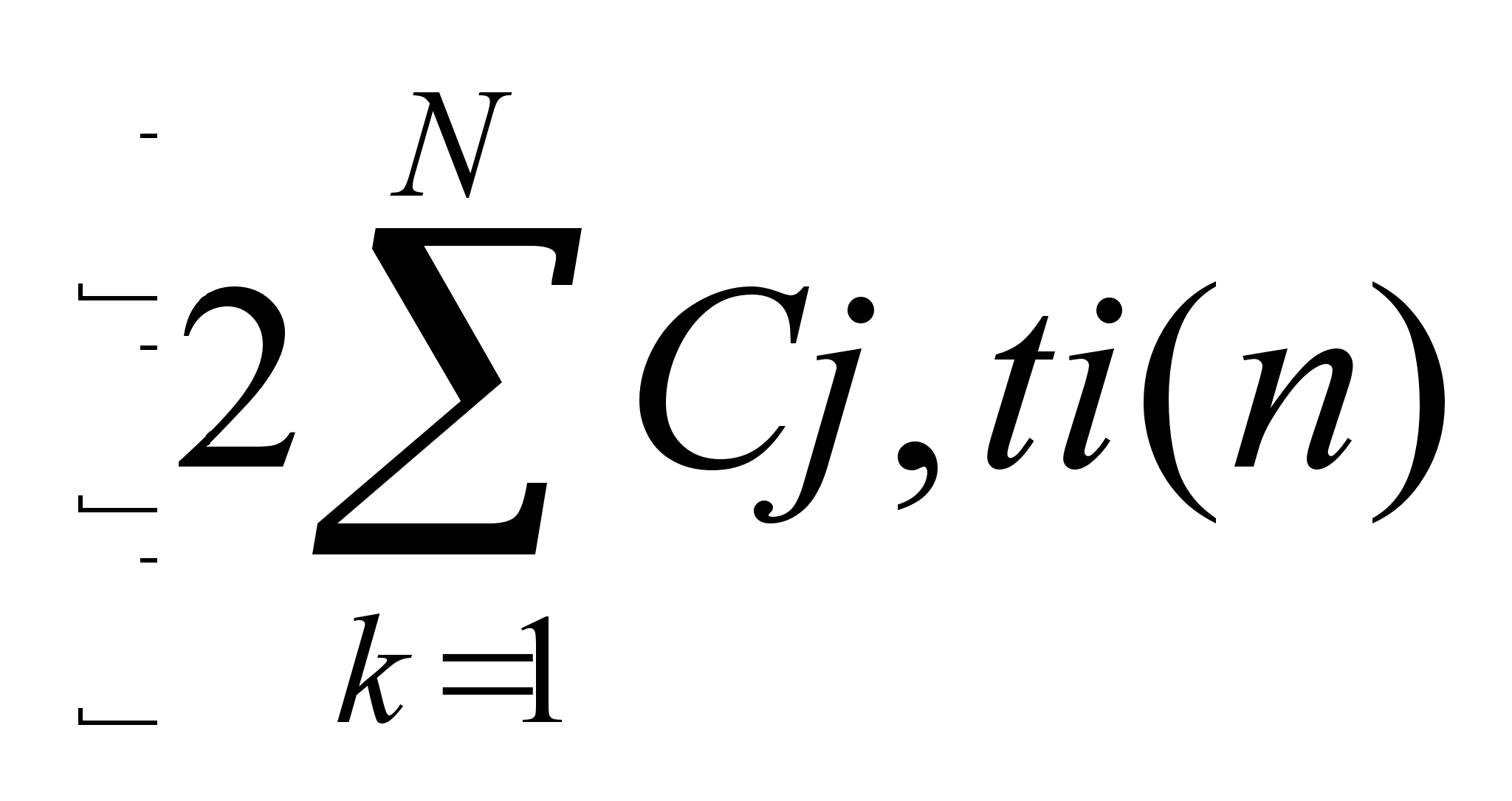 получим
получим
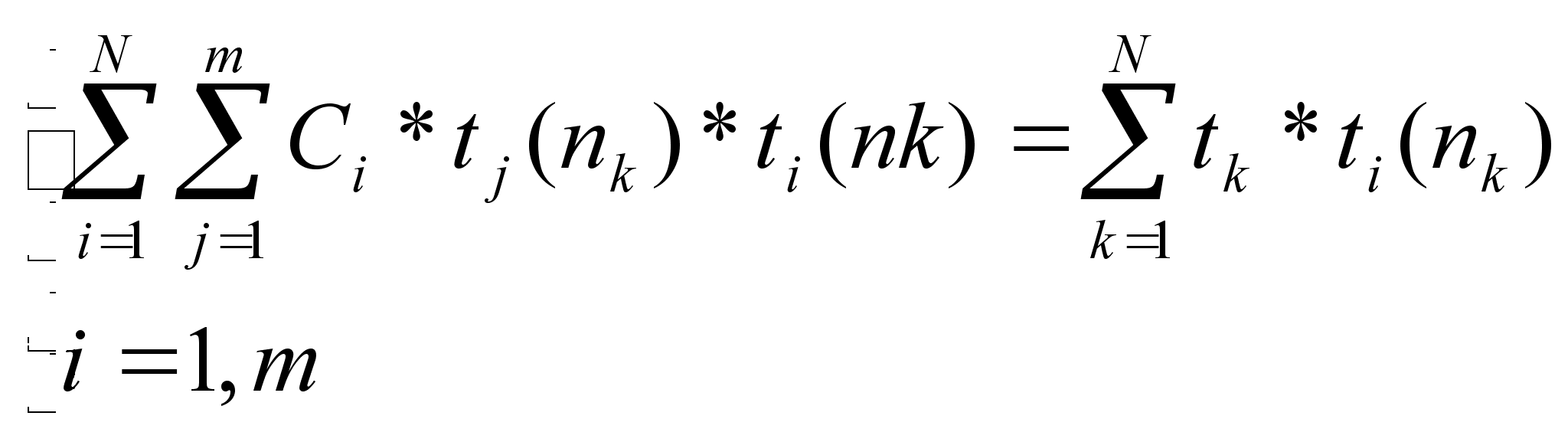
Положим Аij=(ti, tj) и B=(ti,TikTak) => мы получили систему уравнений AX=B, где Х=С. Формирование в матрице столбцов А и столбцов В записывается очень легко используя любой алгоритмический язык. После заполнения матрицы её остаётся решить и вывести решения этой задачи. Решение производиться методом Жордана.
Априорная временная оценка процедур.
Процедура вывода графа на экран в последовательном представлении:
Void prin3(Array *X, int N1, int N)
X – граф в связаном представлении
N – количество вершин графа.
N1 – количество дуг в графе Х O(N,N1)=N*N1Процедура вывода графа на экран в связаном представлении:
Void print3(Spisok **X, int N)
X – граф в связаном представлении
N – количество дуг в графе.
O(N)=NПроцедура вычисления разности графов с возвращающим значением последовательного графа:
Array * RaznostZ(int n, int &n1, Array *X, Spisok **Y,Array *Z)
N - количество дуг графа
N1 – количество вершин в графе Х
X – грав в последовательном представлении
Y - грав в связаном представлении
Z – грав в последовательном представлении
O(N,N1)=N1*N*k=N1*N2
N2 – количество вершин в графе Y
Процедура вычисления разности графов с возвращающим значением последовательного графа:
Spisok * RaznostY(int n, int &n1, Array *X, Spisok **Y)
N - количество дуг графа
N1 – количество вершин в графе Х
X – грав в последовательном представлении
Y - грав в связаном представлении
O(N,N1)=N1*N*(k+l)=N1*(N3+N2)
N2 – количество вершин в графе Y
N3 – количество вершин в графе Z – возвращаемом.
Процедура ввода графов в последовательном представлении:
Spisok **ReadFileY( Spisok **Y, char *st)
St – указатель на строку с именем файла из которого будет происходить ввод
Y - грав в связаном представлении
O(N,N1)=N+N2
N2 – количество вершин в графе Y
Процедура ввода графов в последовательном представлении:
Array *ReadFileY( Array *X, char *st)
St – указатель на строку с именем файла из которого будет происходить ввод
X – грав в последовательном представлении
O(N,N1)=N2
N2 – количество вершин в графе X
Текст программы.
# include
# include
# include
# include
# include
# include
///////////////////////////////////////////////////////////////////////////////////////////////////////
struct Spisok //Связанное представление графа
{ int index; //Содержвтельная "ячейка"
Spisok *next; //Следуюцая "дуга"
};
///////////////////////////////////////////////////////////////////////////////////////////////////////
struct Array //Последовательное представление графа
{ int I; //из какой вершины
int J; //в какую вершину
};
///////////////////////////////////////////////////////////////////////////////////////////////////////
inline double fun1(double N_X,double N_Y,double N_Z){ return N_X*(N_Y+N_Z);}
inline double fun2(double N_X,double N_Y,double N_Z){ return N_X+N_Y;}
inline double fun3(double N_X,double N_Y,double N_Z){ return N_X;}
inline double fun4(double N_X,double N_Y,double N_Z){ return N_Y;}
inline double fun5(double N_X,double N_Y,double N_Z){ return N_Z;}
inline double fun6(double N_X,double N_Y,double N_Z){ return 1;}
///////////////////////////////////////////////////////////////////////////////////////////////////////
const int N = 6, M = N+1;
double A[N][M];
double B[N][M];
typedef double(*MENU1)(double,double,double);
MENU1 MyMenu[6] = { fun1,fun2,fun3,fun4, fun5,fun6 };
////////////////////////////////////////////////////////////////////////////////
int gordanA(int n, int m)
{ int i, j, k, ir;
double s, c;
for (j = 0; j < n; j++){
for (s = 0, i = 0; i < (n - j); i++)if (fabs(A[i][j]) > fabs(s)) s = A[ir = i][j];
if(s==0)return -1;
for (k = j + 1; k < m; k++){
c = A[ir][k]/s;
for (i = 0; i < ir; i++)A[i][k] -= c * A[i][j];
for (i = ir + 1; i < n; i++)A[i - 1][k] = A[i][k] - c * A[i][j];
A[n - 1][k] = c;
}
}
return 0;
}
///////////////////////////////////////////////////////////////////////////////
long double Stp(int a, int n)
{
long double c,bi;
int k;
c=1;
k=n;
bi=a;
while(k>0){
if(k%2==1)c*=bi;
bi*=bi;
k/=2;
}
return c;
}
///////////////////////////////////////////////////////////////////////////////////////////////////////
void CursorOff(void)
{asm{
mov ah,1
mov ch,0x20
int 0x10
}
}
///////////////////////////////////////////////////////////////////////////////////////////////////////
Spisok **GenSeY(int Mas_y,int & Counter)
{ Counter=0;
Spisok **Y = new Spisok* [Mas_y];
for (int i = 0; i< Mas_y; i++){
int m = 0;
int *Pro = new int [Mas_y];
Spisok *beg = NULL, *end = NULL ;
for (int j = 0; j< Mas_y; j++){
int k = random(Mas_y);
int flag = 0;
for (int j = 0; j< m; j++)if (k==Pro[j]) flag = 1;
if (k != 0 && flag == 0){
Pro[m] = k;
m++;
if ((beg==NULL) && (end==NULL)){
end=new(Spisok);
if (end == NULL) {cout next=new (Spisok);
if (end==NULL) {cout index = k;
Counter++;
}
}
Y [i] = beg;
delete [] Pro;
}
return Y;
}
////////////////////////////////////////////////////////////////////////////////
Array *GenSeX(int Mas_y,int & Counter)
{ Counter=0;
Array *X = new Array[Mas_y*Mas_y];
if(X==NULL){cout
Похожие работы
... поиска и устранения в ней ошибок; 4) возможность использования готовых библиотек наиболее употребительных модулей. Но, пожалуй, самым важным достижением структурного подхода к разработке алгоритмов является нисходящее проектирование программ, основанное на идее уровней абстракции, которые становятся уровнями модулей в разрабатываемой программе. На этапе проектирования строится схема иерархии, ...
... данных будет нести больше смысла, если его отсортировать каким‑либо образом. Часто требуется сортировать данные несколькими различными способами. Во‑вторых, многие алгоритмы сортировки являются интересными примерами программирования. Они демонстрируют важные методы, такие как частичное упорядочение, рекурсия, слияние списков и хранение двоичных деревьев в массиве. Наконец, сортировка ...
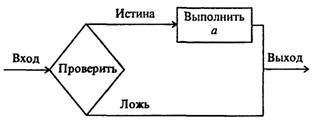
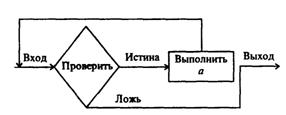
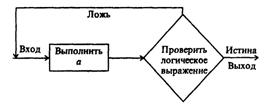
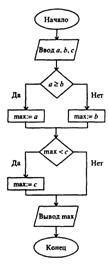
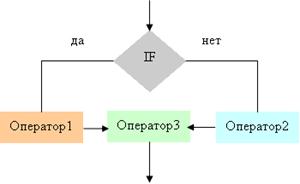
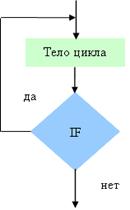
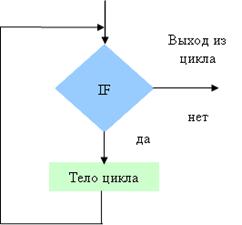
омощью слов и формул. Содержание последовательности этапов выполнения алгоритмов записывается на естественном профессиональном языке предметной области в произвольной форме. Графический способ описания алгоритма (блок - схема) получил самое широкое распространение. Для графического описания алгоритмов используются схемы алгоритмов или блочные символы (блоки), которые соединяются между собой ...
... конкретные примеры, наглядно это обосновывая. Для написания программ необходимо использовать особенные языки. Языки программирования - это нормированные языки, которые служат для описания инструкций обработки, структур данных, а также ввода и вывода данных. Необходимо преобразовывать алгоритм всегда таким образом, чтобы выделять в нем "подалгоритмы". Теория разработки программного обеспечения ...
 Array[ 1 ]
Array[ 1 ]
0 комментариев