 МГТУ
им. Баумана.
МГТУ
им. Баумана.
Факультет Информатики и систем управления.
Кафедра ИУ-2.
Расчетно-пояснительная записка
к дипломной работе на тему:
“Двухосный индикаторный гиростабилизатор телекамеры на ВОГ”
Студент (Носов Н.А.)
Руководитель проекта (Фатеев В.В.)
1996 г.
Введение
Телевизионная техника применяется в различных областях человеческой деятельности - экономике, искусстве, военном деле и многих других. Область ее применения постоянно расширяется. Это объясняет активное развитие в настоящее время телевизионного и кинотехнического оборудования и применение новейших достижений техники при разработке и производстве устройств для различных видов теле и киносъемки.
К таким устройствам относят гироскопические стабилизаторы (ГС) углового положения телекамеры, которые применяются при съемках с подвижных объектов: вертолета, судна, автомобиля, а также с кранов.
Из требований, предъявляемых к этим устройствам, наиболее важными являются следующие:
— высокая точность стабилизации, обусловленная применением объективов с большим фокусным расстоянием;
— дистанционное управление стабилизатором и телекамерой, что связано с целесообразностью или даже необходимостью размещения телекамеры в месте, недоступном для оператора, например, на кране;
— защита от вибрационных возмущений как с целью обеспечения виброустойчивости гиростабилизатора, так и для повышения качества отснятого материала, снижающегося при поступательном движении телекамеры;
— удобство и простота в обращении, необходимость “защиты от дурака”;
— минимально возможные габариты и масса;
— удобство доступа к стабилизируемой камере;
— высокие скорости (до 120 град./с.) и ускорения (до 200 рад./с.) управления, для получения “динамичного” отснятого материала;
— большие углы прокачки, по некоторым осям равные 360°;
— минимально возможное энергопотребление, т.к. для работы часто используются автономные источники питания (аккумуляторы и т.д.).
— большой диапазон балансировок, необходимость которого вызывается использованием различных типов теле и кинокамер с сильно различающимися массогабаритными показателями.
Из устройств, в наибольшей степени удовлетворяющих перечисленным требованиям, в настоящее время известны и применяются следующие. Это силовой гироскопический стабилизатор "Wesscam" (Канада) и трехосные гиростабилизаторы 1ГСП (разработка МВТУ и НИКФИ), 2ГСП, 4ГСП (разработка МВТУ {МГТУ}).
Первый представляет собой платформу, помещенную в карданов подвес, на которой установлены три двухстепенных гироскопа. Компенсация внешнего момента осуществляется разгрузочным двигателем и маятниковым устройством. Сам карданов подвес крепится к основанию с помощью упругой связи, необходимой для аммортизации устройства при поступательных вибрациях вертолета, автомашины и т.п. Гиростабилизатор помещен в защитную сферу имеющую вырез напротив объектива киноаппарата.
Гиростабилизаторы 1ГСП, 2ГСП, 4ГСП индикаторного типа. Все они в качестве чувствительного элемента используют трехстепенный гироскоп типа МГТУ-05. Также все эти три гиростабилизатора имеют дистанционное управление киноаппаратом и пространственным положением стабилизированной платформы.
Особенностью гиростабилизатора 1ГСП является использование внутреннего карданова подвеса и двухконтурной системы стабилизации с применением маховиков совместно с двигателями стабилизации. К недостаткам этого стабилизатора относятся низкая скорость управления (10 град/сек) и отсутствие защиты от аэродинамических воздействий.
В гиростабилизаторе 2ГСП применен наружный карданов подвес с подшипником большого диаметра и также используется двухконтурная система стабилизации (маховик и двигатели стабилизации). Скорость управления до 30 град/сек. Для защиты от аэродинамических воздействий введен следящий частично прозрачный обтекатель, внутри которого расположен трехосный аммортизатор для предохранения платформы с киноаппаратом от линейных вибраций.
Гиростабилизатор 4ГСП также выполнен с наружным кардановым подвесом. Он имеет скорость управления до 60 град/сек., ограниченную, в основном, скоростью управления примененного чувствительного элемента. Защита от аэродинамических нагрузок отсутствует.
В данной работе продолжены исследования по возможности построения гироскопического стабилизатора углового положения телекамеры, в котором:
—скорость управления обеспечивается не менее 100 град/сек;
—предусмотрено дистанционное управление телекамерой и самим гироcтабилизатором;
—в качестве чувствительного элемента использован волоконно-оптический гироскоп.
В частности, рассматриваются вопросы:
—обеспечения устойчивости канала стабилизации при существенно нежесткой конструкции ГС, нежестком креплении телекамеры к ГС и расположении чувствительного элемента не на стабилизируемом объекте;
—проведено исследование инерционных возмущающих моментов, в том числе моментов возникающих от несимметричности конструкции рам ГС;
— проводилась доработка усилителя мощности с ШИМ;
— предложена конструкция датчика угла фазового типа;
— разработана конструкция двухосного ГС.
Обоснование выбора подвеса гиростабилизатора.
Одним из основных факторов, определяющих выбор принципиальной схемы гиростабилизатора телекамеры, является тип карданова подвеса. В гиростабилизаторе телекамеры может быть использован как внутренний, так и наружный карданов подвес. Сравнительный анализ и конструктивная проработка схем подвесов [3] показывает, что применение наружного карданова подвеса для стабилизатора телекамеры представляется более целесообразным. Это объясняется следующими причинами.
Использование наружного карданова подвеса при больших углах прокачки позволяет получить более компактную конструкцию стабилизированной платформы. В этом случае момент инерции платформы относительно собственной оси вращения значительно снижается, и тогда величина максимального момента двигателя стабилизации, выбираемая из условия обеспечения необходимого углового ускорения платформы при управлении может быть уменьшена. Это позволяет повысить точность стабилизации за счет использования двигателя стабилизации меньших габаритов, имеющего меньший момент сухого трения вокруг оси вращения и меньший коэффициент демпфирования.
Габаритные размеры гиростабилизатора телекамеры с наружным кардановым подвесом оказываются меньше, чем с внутренним, т.к. в последнем случае для получения достаточных рабочих углов поворота платформы необходимо выполнение подвеса по гантельной схеме, что приводит к значительному увеличению одного габаритного размера гиростабилизатора по сравнению с другим. Применение наружного карданова подвеса позволяет добиться минимального различия между габаритными размерами гиростабилизатора по взаимноперпендикулярным осям, что является желательным.
В то же время схема гиростабилизатора с наружным кардановым подвесом имеет следующие недостатки:
— увеличенный возмущающий инерционный момент, действующий вокруг оси наружной рамы подвеса, который возникает при переносных поворотах основания гиростабилизатора;
— пониженная жесткость рам наружного карданова подвеса по сравнению с внутренним.
Возмущающий инерционный момент, действующий по оси наружной рамы карданова подвеса, вызывает появление ошибок стабилизации, а также создает дополнительные нагрузки на приводы. Однако, как показывают исследования, в реальных условиях эксплуатации гиростабилизатора киноаппарата на кране и на вертолете [8,9], величина инерционного момента при симметричной конструкции рам оказывается незначительной. В связи с этим первый из перечисленных недостатков наружного карданова подвеса оказывается несущественным.
В представленном двухосном гиростабилизаторе телекамеры применен наружный карданов подвес.
Конструкция подвеса гиростабилизатора позволяет получить угол прокачки по оси тангажа +60...-80 град., а по оси курса угол вращения не ограничен.
Описание особенностей конструкции гиростабилизатора.
Особенностью данного ГС является выполнение наружной рамы в виде Г-образной конструкции. Это позволяет уменьшить габариты ГС и упростить доступ к телекамере. Однако такая конструкция является существенно несимметричной, что вызывает появление дополнительных возмущающих моментов из-за значительных по величине центробежных моментов инерции рам. Исследование этих возмущающих моментов проведено в разделе “Анализ инерционных возмущающих моментов”.
Кроме того, требования по минимизации масс, моментов инерции, требования по динамике управления платформой приводят к тому, что наружная рама оказывается существенно нежесткой. А так как при этом необходимо учитывать требования по высокой точности стабилизации при значительных возмущающих моментах, то возникает необходимость в проведении специальных исследований по вопросам обеспечения устойчивости канала стабилизации. В частности, исследований по расположению ЧЭ в конструкции ГС. Исследование устойчивости канала стабилизации приведено в разделе “Исследование влияния нежесткостей элементов гиростабилизатора на его устойчивость”.
Особенностью данной конструкции ГС является то, что стабилизация положения телекамеры по курсу осуществляется косвенным образом, путем стабилизации положения наружной рамы карданова подвеса. Эта особенность также учтена в разделе “Исследование влияния нежесткостей элементов ГС на его устойчивость”.
Из требований по минимизации энергопотребления вытекает необходимость увеличения КПД канала стабилизации. Согласно этому требованию, а также с целью получения значительных по величине моментов привода, в качестве привода используется редукторный привод со встречным включением двигателей стабилизации серии ДПР. Кроме того, использование в качестве ЧЭ волоконно-оптического гироскопа позволяет снизить энергопотребление собственно ЧЭ до 3 Вт, как в режиме измерения, так и при управлении положением стабилизированной платформы.
Наиболее существенное влияние на КПД электронной части канала стабилизации оказывает коэффициент полезного действия УМ. Поэтому УМ выполнен импульсным, с использованием ШИМ модуляции выходного напряжения. Это позволяет примерно в два раза увеличить КПД УМ по сравнению с линейными схемами УМ. Однако все импульсные УМ являются мощными источниками электромагнитных помех, поэтому в данной конструкции ГС УМ располагается на самом ГС, в непосредственной близости от двигателей стабилизации. Кроме того, непосредственно на ГС расположены схемы защиты ВОГа.
Конструкция крепления телекамеры позволяет проводить установку на платформу телекамер отличающихся по массогабаритным параметрам от базовой на ± 30 %. При этом осуществляется независимая регулировка положения телекамеры по трем взаимоперпендикулярным осям.
Применение в качестве ЧЭ ВОГа вместо механических гироскопов позволяет практически снять ограничения по максимальным скоростям измерения и управления, накладываемых на канал стабилизации самим ЧЭ.
АНАЛИЗ ИНЕРЦИОННЫХ ВОЗМУЩАЮЩИХ МОМЕНТОВ.
При несимметричной конструкции рам гиростабилиза-тора и значительных угловых скоростях движения основания и управления платформой необходимо учитывать возмущающие моменты, вызываемые осевыми и центробежными моментами инерции рам.
В данной работе проводится исследование инерционных возмущающих моментов для двухосного гиростабилизатора, с учетом влияния центробежных моментов инерции рам и скоростей управления платформой.
Выражения для инерционных моментов получены путем раскрытия членов, зависящих от параметров движения основания и платформы входящих в динамические уравнения Эйлера. Основные математические преобразования выполнялись с помощью программы “DERIVE”.
Системы координат и обозначения используемые далее.
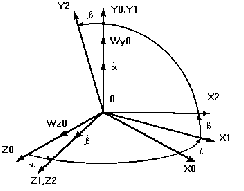
Рис.1.
X0,Y0,Z0 - система координат связанная с основанием.
X1,Y1,Z1 - система координат связанная с наружной
рамой.
X2,Y2,Z2 - система координат связанная с платформой.
Qij - момент количества движения j-го тела по i-й
оси.
wij - угловая скорость j-го тела по i-й оси.
wij' - угловое ускорение j-го тела по i-й оси.
Ji - осевые моменты инерции тела относительно i-й
оси.
Jij - центробежные моменты инерции.
Mij - внешние возмущающие моменты действующие
на j-е тело по i-й оси.
a - угол поворота наружной рамы по оси Y1.
a' - угловая скорость вращения наружной рамы по
оси Y1.
a'' - угловое ускорение наружной рамы по оси Y1.
b - угол поворота платформы по оси Z2.
b' - угловая скорость вращ. платформы по оси Z2.
b'' - угловое ускорение платформы по оси Z2.
Динамические уравнения Эйлера для i-го тела имеют вид:
dQxi/dt - QyiЧwzi + QziЧwyi = Mxi
dQyi/dt - QziЧwxi + QxiЧwzi = Myi
dQyi/dt - QziЧwxi + QxiЧwzi = Myi
В случае двухосного гиростабилизатора эти уравнения преобразуются в следующую форму:
а) для наружной рамы:
dQy1/dt - Qz1Чwx1 + Qx1Чwz1 = My1
б) для платформы:
dQx2/dt - Qy2Чwz2 + Qz2Чwy2 = Mx2
dQy2/dt - Qz2Чwx2 + Qx2Чwz2 = My2 (1)
dQz2/dt - Qx2Чwy2 + Qy2Чwx2 = Mz2
Полный момент количества движения наружной рамы в проекциях на оси X1, Y1, Z1 определяется следующими выражениями:
Qx1 = Jx1Чwx1 - Jxy1Чwy1 - Jxz1Чwz1
Qy1 = Jy1Чwy1 - Jyx1Чwx1 - Jyz1Чwz1 (2)
Qz1 = Jz1Чwz1 - Jzx1Чwx1 - Jzy1Чwy1
Полный момент количества движения платформы в проекциях на оси X2, Y2, Z2 определяется следующими выражениями:
Qx2 = Jx2Чwx2 - Jxy2Чwy2 - Jxz2Чwz2
Qy2 = Jy2Чwy2 - Jyx2Чwx2 - Jyz2Чwz2 (3)
Qz2 = Jz2Чwz2 - Jzx2Чwx2 - Jzy2Чwy2
Кинематические уравнения двухосного гиростаби-лизатора, для расположения координатных осей приве-денного на рис.1, имеют вид:
а) для наружной рамы:
wx1 = wx0Чcos(a) - wz0Чsin(a)
wy1 = wy0 + a' (4*)
wz1 = wx0Чsin(a) + wz0Чcos(a)
wx1' = wx0'Чcos(a) - wz0'Чsin(a)
wy1' = wy0' + a'' (4*')
wz1' = wx0'Чsin(a) + wz0'Чcos(a)
б) для платформы:
wx2 = wx1Чcos(b) + wy1Чsin(b)
wy2 = wy1Чcos(b) - wx1Чsin(b) (5*)
wz2 = wz1 + b'
wx2' = wx1'Чcos(b) + wy1'Чsin(b)
wy2' = wy1'Чcos(b) - wx1'Чsin(b) (5*')
wz2' = wz1' + b''
Из 2-го уравнения в (5*) следует, что:
wy1=wx1Чtg(b)+wy2/cos(b)
Из 2-го уравнения в (5*') следует, что:
wy1'=wx1'Чtg(b)+wy2'/cos(b)
Тогда, учитывая, что wy2, wz2, wy2', wz2' являются параметрами движения стабилизированного объекта, т.е. заданы, кинематические уравнения можно переписать в следующем виде:
wx1 = wx0Чcos(a) - wz0Чsin(a)
wy1 = wx1Чtg(b)+wy2/cos(b) (4)
wz1 = wx0Чsin(a) + wz0Чcos(a)
wx1' = wx0'Чcos(a) - wz0'Чsin(a)
wy1' = wx1'Чtg(b)+wy2'/cos(b) (4')
wz1' = wx0'Чsin(a) + wz0'Чcos(a)
wx2 = wx1Чcos(b) + wy1Чsin(b) (5)
wx2' = wx1'Чcos(b) + wy1'Чsin(b) (5')
Подставляя выражения для полных моментов количества движения (2), (3) в динамические уравнения Эйлера (1), получаем следующий вид уравнений движения наружной рамы и платформы:
Jy1Чwy1' + (Jx1-Jz1)Чwx1Чwz1 + Jzx1Чwx12 - Jxz1Чwz12 +
+ Jzy1Чwx1Чwy1 - Jxy1Чwy1Чwz1 - Jyx1Чwx1' - Jyz1Чwz1' = My1 (6.1)
Jx2Чwx2' + (Jz2-Jy2)Чwy2Чwz2 - 2ЧJzyЧwy22 + Jyz2Чwz22 +
+ Jyx2Чwx2Чwz2 - Jzx2Чwx2Чwy2 - Jxz2Чwz2' - Jxy2Чwy2' = Mx2 (6.2)
Jy2Чwy2' + (Jx2-Jz2)Чwx2Чwz2 + Jzx2Чwx22 - Jxz2Чwz22 +
+ Jzy2Чwx2Чwy2 - Jxy2Чwy2Чwz2 - Jyx2Чwx2' - Jyz2Чwz2' = My2 (6.3)
Jz2Чwz2' + (Jy2-Jx2)Чwx2Чwy2 + Jxy2Чwy22 - Jyx2Чwx22 +
+ Jxz2Чwy2Чwz2 - Jyz2Чwx2Чwz2 - Jzx2Чwx2' - Jzy2Чwy2' = Mz2 (6.4)
При отсутствии моментов внешних сил правые части уравнений (6.2), (6.3), (6.4) обращаются в нуль, а правая часть (6.1) представляет собой момент реакции со стороны платформы на внешнюю раму вокруг оси Y1. Обозначив левые части уравнений (6.1), (6.2), (6.3) буквами A, B и C, соответственно, получаем выражение для полного инерционного момента относительно оси внешней рамы:
My1ин = A + B Ч sin(b) + C Ч cos(b) (7)
Раскрыв в (7) сокращения A, B и C и преобразовав получаем выражение для полного инерционного момента Мy1ин.
Мy1ин=Jxz1·{wx12-wz12}+
+Jxz2·cos(b)·wx22-Jyz2·sin(b)·wy22+
+{Jyz2·sin(b)-Jxz2·cos(b)}·wz22+
+{Jyz2·cos(b)-Jxz2·sin(b)}·wx2·wy2+
+{Jxy2·sin(b)+(Jx2-Jz2)·cos(b)}·wx2·wz2+
+{(Jz2-Jy2)·sin(b)-Jxy2·cos(b)}·wz2·wy2+ (8)
+{Jx2·sin(b)-Jxy2·cos(b)}·wx2' +
+{Jy2·cos(b)-Jxy2·sin(b)}·wy2'-
-{Jxz2·sin(b)+Jyz2·cos(b)}·wz2'+
+Jyz1·wx1·wy1-
-Jxy1·wz1·wy1+
+(Jx1-Jz1)·wx1·wz1 -
-Jxy1·wx1'-
-Jyz1·wz1'+
+Jy1·wy1'
После подстановки в полученные выражения для инерционных моментов Мy1ин, Mz2ин кинематических уравнений (4), (4'), (5), (5') и преобразования, получим следующий вид выражений для Мy1ин, Mz2ин:
MZ2ИН={cos(2·b)-2}·cos(a)2·tg(b)2·Jxy2(·wx02+wz02)+
+{2·tg(b)2·sin(b)2-2·cos(b)2+4}·sin(a)·cos(a)·Jxy2·wx0·wz0+
+{(Jy2-Jx2)/cos(b)-2·Jxy2·sin(b)(1+tg(b)2)}·cos(a)·wx0·wy2+
+Jyz2·wz0·wz2·(sin(a)-cos(a))/cos(b)-
-Jxz2·wx0'·cos(a)/cos(b)+
+{2·Jxy2·(sin(b)·tg(b)2+sin(b))·sin(a)+(Jx2-Jy2)·sin(a)/cos(b)}·wy2·wz0+
+Jxz2·wz0'·sin(a)/cos(b)+
+{Jxz2-Jyz2}·wy2·wz2·tg(b)+
+{(Jy2-Jx2)·tg(b)+Jxy2·(1-tg(b)2)}·wy22-
-{Jxz2·tg(b)+Jyz2}·wy2'+
+Jz2·wz2'
(9)
My1ин={[Jxz2·(tg(b)4+2/cos(b)2-1)·cos(b)3+Jyz1·tg(b)+Jxz1]·cos(a)2+
+[[(Jx1-Jz1)-Jxy1·tg(b)]·cos(a)-Jxz1·sin(a)]·sin(a)}·wx02+
+{[[Jxy1·tg(b)+(Jz1-Jx1)]·sin(a)-Jxz1·cos(a)]·cos(a)+
+[Jxz2·cos(b)3·[2/cos(b)2+tg(b)4-1]+Jyz1·tg(b)+Jxz1]·sin(a)2}·wz02+
+{(Jx1-Jz1)·cos(2·a)+[1-tg(b)4-2/cos(b)2]·Jxz2·cos(b)3·sin(2·a)-
-[Jyz1·tg(b)+2·Jxz1]·2·sin(a)·cos(a)-
-Jxy1·tg(b)·cos(2·a)}·wx0·wz0+
+{[Jxy2·sin(b)·cos(b)(tg(b)2+1)+(Jx2-Jz2)]·cos(a)}·wx0·wz2+
+{[Jxz2·sin(b)·cos(b)+Jxz2·sin(b)3/cos(b)+Jyz2]·cos(a)+
+[Jyz1·cos(a)-Jxy1·sin(a)]/cos(b)}·wx0·wy2-
-{[Jxz2·sin(b)·cos(b)·(1+tg(b)2)+Jyz2]·sin(a)+
+[Jyz1·sin(a)+Jxy1·cos(a)]/cos(b)}·wz0·wy2+
+{-[tg(b)2+1]·sin(b)·cos(b)·Jxy2+(Jz2-Jx2)]·sin(a)}·wz0·wz2+
+{[Jx2·sin(b)·cos(b)·(1+tg(b)2)+Jy1·tg(b)-(Jxy1+
+Jxy2)]·cos(a)-Jyz1·sin(a)}·wx0'+
+{[-Jx2·sin(b)·cos(b)·(1+tg(b)2)+(Jxy1+Jxy2)-
-Jy1·tg(b)]·sin(a)-Jyz1·cos(a)}·wz0'+
+{Jyz2·sin(b)-Jxz2·cos(b)]·wz22-
-{Jxz2·sin(b)+Jyz2·cos(b)}·wz2'+
+{(Jx2-Jy2)·sin(b)+Jxy2·cos(b)·(tg(b)2-1)}·wz2·wy2+
+{Jx2·sin(b)2/cos(b)-2·Jxy2·sin(b)+Jy2·cos(b)+Jy1/cos(b)}·wy2'
Анализ инерционных возмущающих моментов для различных режимов работы гиростабилизатора.Численный анализ инерционных возмущающих моментов (9) провожу для различных режимов работы ГС, типовая конструкция которого приведена на рис 2.
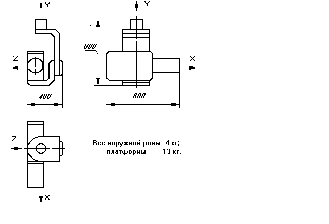
Рис.2.
Пусть ГС имеет следующие инерционные параметры наружной рамы и платформы:
Jx1 = -------//------ Jx2= 2000 гсмс2 = 0.2 кгм2
Jy1 = 1500 гсмс2 = 0.15 кгм2 Jy2= 9500 гсмс2 = 0.95 кгм2
Jz1 = -------//------ Jz2 = 10000 гсмс2 = 1 кгм2
Jxy1 = Jyx1 = 0 Jxy2 = Jyx2 = 0.0085 кгм2
Jxz1 = Jzx1 = 0 Jxz2 = Jzx2 = 0.023 кгм2
Jzy1 = Jyz1 =1500 гсмс2 = 0.15 кгм2 Jzy2 = Jyz2 = 0.04 кгм2
Угловые скорости и ускорения основания и управления платформой принимаю равными их типовым значениям при работе гиростабилизатора на кране.
wx0 = ±1 рад/с wy2 = ±2 рад/с
wy0 = ±1 рад/с wz2 = ±2 рад/с
wz0 = ±1 рад/с wy2' = ±3 рад/с2 (10)
wx0'= ±0,2 рад/с2 wz2' = ±3 рад/с2
wy0'= ±0,2 рад/с2
wz0'= ±0,2 рад/с2
Углы прокачки рам изменяются в диапазоне:
a = ± 2 рад. » ± 120 град. (10)
b = ±1 рад. » ± 60 град.
Исследование величины численных значений инерционных возмущающих моментов провожу с помощью программы “MOMIN” листинг которой приведен в “Приложении 1”.
Анализ инерционных возмущающих моментов провожу для следующих случаев работы гиро-стабилизатора:
1) Работа на неподвижном основании при наличии скоростей управления платформой;
2) Работа на подвижном основании при неподвижной платформе;
3) Работа на подвижном основании при управляемой платформе;
1) Работа ГС на неподвижном основании при управляемой платформе,
т.е. при условии:
wx0 = wy0 = wz0 = wx0' = wy0' = wz0' = 0 (11)
a № 0; b № 0; wy2№ 0; wz2 № 0; wy2' № 0; wz2' № 0
Тогда подставляя (11) в выражения для инерционных моментов (9), получаем следующий их вид:
MZ2ИН=+{Jxz2-Jyz2}·wy2·wz2·tg(b)+
+{(Jy2-Jx2)·tg(b)+Jxy2·(1-tg(b)2)}·wy22-
-{Jxz2·tg(b)+Jyz2}·wy2'+
+Jz2·wz2'
MY1ИН=+{Jyz2·sin(b)-Jxz2·cos(b)}·wz22-
-{Jxz2·sin(b)+Jyz2·cos(b)}·wz2'+
+{(Jx2-Jy2)·sin(b)+Jxy2·cos(b)·(tg(b)2-1)}·wz2·wy2+
+{Jx2·sin(b)2/cos(b)-
-2·Jxy2·sin(b)+Jy2·cos(b)+Jy1/cos(b)}·wy2'
Максимальные значения инерционных моментов, полученные при выполнении условий (10), следующие:
а) ось Y1: Мy1ин = Мин + Мцб = 5.68 + 0.14 = 5.82 НЧм.
при a = 0.067 рад.
b = 1 рад.
wy2 = -2.0 рад/с.
wy2' = 3.0 рад/с2.
wz2 = 2 рад/с.
wz2' = -3.0 рад/с2.
где Мин - вклад в Мy1ин возмущающих моментов, связаных с осевыми моментами инерции наружной рамы и платформы;
Мцб - вклад в Мy1ин возмущающих моментов, связаных с центробежными моментами инерции наружной рамы и платформы;
Вклад Мцб в суммарный возмущающий момент составил:
Мцб
![]() К
= Ч
100% = 2.38 %
К
= Ч
100% = 2.38 %
Мин + Мцб
б) ось Z2: Мz2ин = Мин + Мцб = 7.67 + 0.33 = 8.0 НЧм.
при a = 0.067 рад.
b = 1 рад.
wy2 = 2.0 рад/с.
wy2' = -3.0 рад/с2.
wz2 = -2 рад/с.
wz2' = 3.0 рад/с2.
Вклад Мцб в суммарный возмущающий момент составил:
Мцб
![]() К
= Ч
100% = 4.2 %
К
= Ч
100% = 4.2 %
Мин + Мцб
2) Работа ГС на подвижном основании при неподвижной платформе,
т.е. при:
wy2= wy2'= wz2 = wz2' = 0; a № 0; b № 0; (12)
wx0 № 0; wy0 № 0; wz0 № 0; wx0' № 0; wy0' № 0; wz0' № 0
Тогда подставляя (12) в выражения для инерционных моментов (9) получаем следующий их вид:
MZ2ИН={cos(2·b)-2}·cos(a)2·tg(b)2·Jxy2(·wx02+wz02)+
+{2·tg(b)2·sin(b)2-2·cos(b)2+4}·sin(a)·cos(a)·Jxy2·wx0·wz0+
-Jxz2·wx0'·cos(a)/cos(b)+
+Jxz2·wz0'·sin(a)/cos(b)+
MY1ИН={[Jxz2·(tg(b)4+2/cos(b)2-1)·cos(b)3+Jyz1·tg(b)+
+Jxz1]·cos(a)2+
+[[(Jx1-Jz1)-Jxy1·tg(b)]·cos(a)-Jxz1·sin(a)]·sin(a)}·wx02+
+{[[Jxy1·tg(b)+(Jz1-Jx1)]·sin(a)-Jxz1·cos(a)]·cos(a)+
+[Jxz2·cos(b)3·[2/cos(b)2+tg(b)4-1]+Jyz1·tg(b)+
+Jxz1]·sin(a)2}·wz02+
+{(Jx1-Jz1)·cos(2·a)+[1-tg(b)4-2/cos(b)2]·Jxz2·cos(b)3·
·sin(2·a)-[Jyz1·tg(b)+2·Jxz1]·2·sin(a)·cos(a)-
-Jxy1·tg(b)·cos(2·a)}·wx0·wz0+
+{[Jx2·sin(b)·cos(b)·(1+tg(b)2)+Jy1·tg(b)-(Jxy1+Jxy2)]·cos(a)-
-Jyz1·sin(a)}·wx0'+
+{[-Jx2·sin(b)·cos(b)·(1+tg(b)2)+(Jxy1+Jxy2)-Jy1·tg(b)]·sin(a)-
-Jyz1·cos(a)}·wz0'+
При этом получены следующие максимальные значения инерционных возмущающих моментов:
а) ось Y1:
Мy1ин = Мин + Мцб = 0.154 + 0.551= 0.705 НЧм.
при a = - 0.82 рад.
b = 1 рад.
wx0 = wz0 = 1 рад/с.
wx0' = wz0' = 0.2 рад/с2.
wy0 = 0.167 рад/c.
wy0' = 0.167 рад/с2.
Вклад Мцб в суммарный возмущающий момент составил:
Мцб
![]() К
= Ч
100 % = 78.14 %
К
= Ч
100 % = 78.14 %
Мин + Мцб
б) ось Z2:
Мz2ин = Мин + Мцб = 0 + 0.07= 0.07 НЧм.
при a = - 0.785 рад.
b = 1 рад.
wx0 = wz0 = 1 рад/с.
wx0' = wz0' = 0.2 рад/с2.
wy0 = 0.167 рад/с.
wy0' = 0.167 рад/c2
Вклад Мцб в суммарный возмущающий момент составил:
Мцб
![]() К
= Ч
100 % = 100 %
К
= Ч
100 % = 100 %
Мин + Мцб
3) Работа ГС на подвижном основании при управляемой платформе.
При подвижном основании и управляемой платформе инерционные возмущающие моменты определяются выражениями (9).
MZ2ИН={cos(2·b)-2}·cos(a)2·tg(b)2·Jxy2(·wx02+wz02)+
+{2·tg(b)2·sin(b)2-2·cos(b)2+4}·sin(a)·cos(a)·Jxy2·wx0·wz0+
+{(Jy2-Jx2)/cos(b)-2·Jxy2·sin(b)(1+tg(b)2)}·cos(a)·wx0·wy2+
+Jyz2·wz0·wz2·(sin(a)-cos(a))/cos(b)-
-Jxz2·wx0'·cos(a)/cos(b)+
+{2·Jxy2·(sin(b)·tg(b)2+sin(b))·sin(a)+(Jx2-
-Jy2)·sin(a)/cos(b)}·wy2·wz0+
+Jxz2·wz0'·sin(a)/cos(b)+
+{Jxz2-Jyz2}·wy2·wz2·tg(b)+
+{(Jy2-Jx2)·tg(b)+Jxy2·(1-tg(b)2)}·wy22-
-{Jxz2·tg(b)+Jyz2}·wy2'+
+Jz2·wz2'
MY1ИН={[Jxz2·(tg(b)4+2/cos(b)2-1)·cos(b)3+Jyz1·tg(b)+
+Jxz1]·cos(a)2+
+[[(Jx1-Jz1)-Jxy1·tg(b)]·cos(a)-Jxz1·sin(a)]·sin(a)}·wx02+
+{[[Jxy1·tg(b)+(Jz1-Jx1)]·sin(a)-Jxz1·cos(a)]·cos(a)+
+[Jxz2·cos(b)3·[2/cos(b)2+tg(b)4-1]+
+Jyz1·tg(b)+Jxz1]·sin(a)2}·wz02+
+{(Jx1-Jz1)·cos(2·a)+[1-tg(b)4-2/cos(b)2]·Jxz2·cos(b)3·
·sin(2·a)-[Jyz1·tg(b)+2·Jxz1]·2·sin(a)·cos(a)-
-Jxy1·tg(b)·cos(2·a)}·wx0·wz0+
+{[Jxy2·sin(b)·cos(b)(tg(b)2+1)+(Jx2-Jz2)]·cos(a)}·wx0·wz2+
+{[Jxz2·sin(b)·cos(b)+Jxz2·sin(b)3/cos(b)+Jyz2]·cos(a)+
+[Jyz1·cos(a)-Jxy1·sin(a)]/cos(b)}·wx0·wy2-
-{[Jxz2·sin(b)·cos(b)·(1+tg(b)2)+Jyz2]·sin(a)+
+[Jyz1·sin(a)+Jxy1·cos(a)]/cos(b)}·wz0·wy2+
+{-[tg(b)2+1]·sin(b)·cos(b)·Jxy2+(Jz2-Jx2)]·sin(a)}·wz0·wz2+
+{[Jx2·sin(b)·cos(b)·(1+tg(b)2)+Jy1·tg(b)-(Jxy1+Jxy2)] ·
·cos(a)-Jyz1·sin(a)}·wx0'+
+{[-Jx2·sin(b)·cos(b)·(1+tg(b)2)+(Jxy1+Jxy2)-Jy1·tg(b)]·
·sin(a)-Jyz1·cos(a)}·wz0'+
+{Jyz2·sin(b)-Jxz2·cos(b)}·wz22-
-{Jxz2·sin(b)+Jyz2·cos(b)}·wz2'+
+{(Jx2-Jy2)·sin(b)+Jxy2·cos(b)·(tg(b)2-1)}·wz2·wy2+
+{Jx2·sin(b)2/cos(b)-2·Jxy2·sin(b)+Jy2·cos(b)+
+Jy1/cos(b)}·wy2'
При этом получены следующие максимальные значения инерционных моментов.
а) ось Y1:
Мy1ин = Мин + Мцб = 8.1 + 1.65 = 9.75 НЧм
при a = 0.776 рад.
b = 1.0 рад.
wy2 = -2 рад/с.
wy2' = 3 рад/с2.
wz2 = 2 рад/с.
wz2' = -3 рад/с2.
wx0 = wz0 = 1 рад/c.
wx0' = 0.2 рад/c2.
wz0' = - 0.2 рад/c2.
wy0 = 0.167 рад/c.
wy0' = 0.167 рад/c2.
Вклад Мцб в суммарный возмущающий момент составил:
Мцб
![]() К
= Ч
100 % = 16.9 %
К
= Ч
100 % = 16.9 %
Мy1ин+Мцб
б) ось Z2:
Мz2ин = Мин + Мцб = 11.6 + 0.361 = 11.96 НЧм
при a = -0.785 рад.
b = 1.0 рад.
wy2 = 2 рад/с.
wy2' = -3 рад/с2.
wz2 = -2 рад/с.
wz2' = 3 рад/с2.
wx0 =wz0 = 1 рад/c.
wx0' = wz0' = - 0.2 рад/c2.
wy0 = 0.167 рад/c.
wy0' = 0.167 рад/c2.
Вклад Мцб в суммарный возмущающий момент составил:
Мцб
![]() К
= Ч
100 % = 3.02 %
К
= Ч
100 % = 3.02 %
Мy1ин + Мцб
Исследование влияния нежесткостей элементов гиростабилизатора на его устойчивость.
Анализ устойчивости ГС с нежесткими наружной рамой, креплением статора двигателя стабилизации к раме, с нежесткими редуктором и связью платформы с объектом стабилизации, проводим основываясь на следующей физической модели:
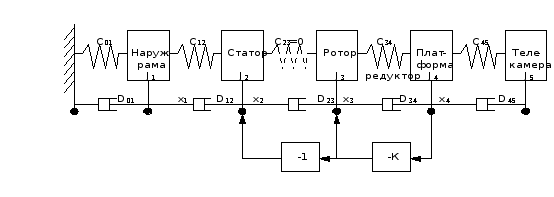
Рис. 1.
здесь Ji - момент инерции i-го элемента;
Ci,j - коэффициент упругости;
Di,j - коэфф. демпфирования между i и j
элементами;
K - коэффициент передачи цепи обратной
связи.
Оценку влияния каждого из входящих в модель элементов (Ji,Ci,j,Di,j) выполняем на основе анализа поведения ЛАХ разомкнутой системы, при вариациях Ji,Ci,j,Di,j.
Уравнения движения каждого из элементов модели в общем виде могут быть представлены следующим образом:
JiЧxi''+Di-1,iЧ(xi'-xi-1')-Di,i+1Ч(xi+1'-xi')+Ci-1,iЧ (xi-xi-1)-Ci,i+1Ч(xi+1 - xi) = Мi (1)
где Мi - внешний момент действующий на i-й элемент;
xi,xi', xi''- перемещение, скорость и ускорение i-го
элемента.
Расписав уравнение (1) для каждого элемента, получим следующюю систему уравнений движения модели:
J1Чx1''+D01Ч(x1'-x0')-D12Ч(x2'-x1')+C01Ч(x1-x0)-C12Ч(x2-x1)= М1
J2Чx2''+D12Ч(x2'-x1')-D23Ч(x3'-x2')+C12Ч(x2-x1)-C23Ч(x3-x2)= М2
J3Чx3''+D23Ч(x3'-x2')-D34Ч(x4'-x3')+C23Ч(x3-x2)-C34Ч(x4-x3)= М3 (2)
J4Чx4''+D34Ч(x4'-x3')-D45Ч(x5'-x4')+C34Ч(x4-x3)-C45Ч (x5-x4)= М4
J5Чx5''+D45Ч(x5'-x4')-D56Ч(x6'-x5')+C45Ч(x5-x4)-C56Ч(x6-x5)= М5
Раскрыв в (2) скобки и преобразовав получаем следующий вид уравнений движения модели.
-D01Чx0'-C01Чx0+J1Чx1''+(D01+D12)Чx1'+(C01+C12)Чx1-D34Чx2'-
-C12Чx2= М1
-D12Чx1'-C12Чx1+J2Чx2''+(D23+D12)Чx2'+(C12+C23)Чx2-D23Чx3'-
-C23Чx3= М2
-D23Чx2'-C23Чx2+J3Чx3''+(D23+D34)Чx3'+(C23+C34)Чx3-D34Чx4'-
-C34Чx4=М3 (3)
-D34Чx3'-C34Чx3+J4Чx4''+(D34+D45)Чx4'+(C34+C45)Чx4-D45Чx5'-
-C45Чx5= М4
-D45Чx4'-C45Чx4+J5Чx5''+(D45+D56)Чx5'+(C45+C56)Чx5-D56Чx6'-
-C56Чx6= М5
Переписав (3) в операторной форме получаем уравнения движения модели в следующем виде.
-(D01Чs+C01)Чx0+(J1Чs2+(D01+D12)Чs+(C01+C12))Чx1 -
-(D12Чs+C12)Чx2= М1
-(D12Чs+C12)Чx1+(J2Чs2+(D12+D23)Чs+(C12+C23))Чx2-
-(D23Чs+C23)Чx3= КЧx4
-(D23Чs+C23)Чx2+(J3Чs2+(D23+D34)Чs+(C23+C34))Чx3-
-(D34Чs+C34)Чx4=-КЧx4
-(D34Чs+C34)Чx3+(J4Чs2+(D34+D45)Чs+(C34+C45))Чx4-
-(D45Чs+C45)Чx5= М4 (4)
-(D45Чs+C45)Чx4+(J5Чs2+(D45+D56)Чs+(C45+C56))Чx5-
-(D56Чs+C56)Чx6= М5
Для нахождения передаточной функции разомкнутой системы по управляющему воздействию Wp(s) составим два определителя: главный - D, и характеризующий входное воздействие D1, с учетом того, что x0=0; D56=0; C56=0; C23=0.
![]()
![]()
a11 a12 0 0 0
a21 a22 a23 0 0
D= 0 a32 a33 a34 0 (5)
0 0 a43 a44 a45
0 0 0 a54 a55
где a11 = J1Чs2+(D01+D12)Чs+C01+C12
a12 = -D12Чs-C12
a21 = a12
a22 = J2Чs2+(D12+D23)Чs+C12
a23 = -D23Чs
a32 = a23
a33 = J3Чs2+(D23+D34)Чs+C34
a34 = -D34Чs-C34
a43 = a34
a44 = J4Чs2+(D34+D45)Чs+C34+C45
a45 = -D45Чs-C45
a54 = a45
a55 = J5Чs2+D45Чs+C45
![]()
![]() a11 a12 0 0 0
a11 a12 0 0 0
a21 a22 a23 -KЧx4 0
D1= 0 a32 a33 KЧx4 0 (6)
0 0 a43 0 a45
0 0 0 0 a55
Передаточная функция разомкнутой системы определяется как:
![]() D1 -KЧ(b7Чs7+....+b1Чs+b0)Чx4
D1 -KЧ(b7Чs7+....+b1Чs+b0)Чx4
![]()
![]() Wp(s)
= = (7)
Wp(s)
= = (7)
![]() DЧx4
sЧ(a9Чs9+....+a1Чs+a0)Чx4
DЧx4
sЧ(a9Чs9+....+a1Чs+a0)Чx4
Коэффициенты ai, bi полиномов числителя и знаменателя передаточной функции Wp(s) выражаются через параметры элементов модели следующим образом:
(8)
a9=J1J2J3J4J5
a8=D01J2J3J4J5+D12J3J4J5(J1+J2)+J1(D23J4J5(J2+J3)+J2(D34J5(J3+J4)+D45J3(J4+J5)))
a7=C01J2J3J4J5+C12J3J4J5(J1+J2)+C34J1J2(J3J5+J4J5)+C45J1J2J3(J4+J5)+D01(D12J3J4J5+D23J4J5(J2+J3)+J2(D34J5(J3+J4)+D45J3(J4+J5)))+D12(D23J4J5(J1+J2+J3)+(J1+J2)(D34J5(J3+J4)+D45J3(J4+J5)))+J1(D23(D34J5(J2+J3+J4)+D45(J4+J5)(J2+J3))+D34D45J2(J3+J4+J5))
a6=C01(D12J3J4J5+D23J4J5(J2+J3)+J2(D34J5(J3+J4)+D45J3(J4+J5)))+C12(D01J3J4J5+D23J4J5(J1+J2+J3)+(J1+J2)(D34J5(J3+J4)+D45J3(J4+J5)))+C34(D01J2(J3J5+J4J5)+D12J5(J3+J4)(J1+J2)+J1(D23J5(J2+J3+J4)+D45J2(J3+J4+J5)))+C45(D01J2J3(J4+J5)+D12J3(J4+J5)(J1+J2)+J1(D23(J4+J5)(J2+J3)+D34J2(J3+J4+J5)))+D01(D12(D23J4J5+D34(J3J5+J4J5)+D45J3(J4+J5))+D23(D34(J2J5+J3J5+J4J5)+D45(J4+J5)(J2+J3))+D34D45J2(J3+J4+J5))+D12(D23(D34(J1J5+J2J5+J3J5+J4J5)+D45(J4+J5)(J1+J2+J3))+D34D45(J3+J4+J5)(J1+J2))+D23D34D45J1(J2+J3+J4+J5)
a5=C01(C12J3J4J5+C34J2(J3J5+J4J5)+C45J2J3(J4+J5)+D12(D23J4J5+D34(J3J5+J4J5)+D45J3(J4+J5))+D23(D34(J2J5+J3J5+J4J5)+D45(J4+J5)(J2+J3))+D34D45J2(J3+J4+J5))+C12(C34J5(J3+J4)(J1+J2)+C45J3(J4+J5)(J1+J2)+D01(D23J4J5+D34(J3J5+J4J5)+D45J3(J4+J5))+D23(D34(J1J5+J2J5+J3J5+J4J5)+D45(J4+J5)(J1+J2+J3))+D34D45(J3+J4+J5)(J1+J2))+C34(C45J1J2(J3+J4+J5)+D01(D12(J3J5+J4J5)+D23(J2J5+J3J5+J4J5)+D45J2(J3+J4+J5))+D12(D23(J1J5+J2J5+J3J5+J4J5)+D45(J3+J4+J5)(J1+J2))+D23D45J1(J2+J3+J4+J5))+C45(D01(D12J3(J4+J5)+D23(J2(J4+J5)+J3(J4+J5))+D34J2(J3+J4+J5))+D12(D23(J1(J4+J5)+J2(J4+J5)+J3(J4+J5))+D34(J3+J4+J5)(J1+J2))+D23D34J1(J2+J3+J4+J5))+D01(D12(D23(D34J5+D45(J4+J5))+D34D45(J3+J4+J5))+D23D34D45(J2+J3+J4+J5))+D12D23D34D45(J1+J2+J3+J4+J5)
a4=C01(C12(D23J4J5+D34(J3J5+J4J5)+D45J3(J4+J5))+C34(D12(J3J5+J4J5)+D23(J2J5+J3J5+J4J5)+D45J2(J3+J4+J5))+C45(D12J3(J4+J5)+D23(J2(J4+J5)+J3(J4+J5))+D34J2(J3+J4+J5))+D12(D23(D34J5+D45(J4+J5))+D34D45(J3+J4+J5))+D23D34D45(J2+J3+J4+J5))+C12(C34(D01(J3J5+J4J5)+D23(J1J5+J2J5+J3J5+J4J5)+D45(J3+J4+J5)(J1+J2))+C45(D01J3(J4+J5)+D23(J1(J4+J5)+J2(J4+J5)+J3(J4+J5))+D34(J3+J4+J5)(J1+J2))+D01(D23(D34J5+D45(J4+J5))+D34D45(J3+J4+J5))+D23D34D45(J1+J2+J3+J4+J5))+C34(C45(D01J2(J3+J4+J5)+D12(J1(J3+J4+J5)+J2(J3+J4+J5))+D23J1(J2+J3+J4+J5))+D01(D12(D23J5+D45(J3+J4+J5))+D23D45(J2+J3+J4+J5))+D12D23D45(J1+J2+J3+J4+J5))+C45(D01(D12(D23(J4+J5)+D34(J3+J4+J5))+D23D34(J2+J3+J4+J5))+D12D23D34(J1+J2+J3+J4+J5))+D01D12D23D34D45
a3=C01(C12(C34(J3J5+J4J5)+C45J3(J4+J5)+D23(D34J5+D45(J4+J5))+D34D45(J3+J4+J5))+C34(C45J2(J3+J4+J5)+D12(D23J5+D45(J3+J4+J5))+D23D45(J2+J3+J4+J5))+C45(D12(D23(J4+J5)+D34(J3+J4+J5))+D23D34(J2+J3+J4+J5))+D12D23D34D45)+C12(C34(C45(J1(J3+J4+J5)+J2(J3+J4+J5))+D01(D23J5+D45(J3+J4+J5))+D23D45(J1+J2+J3+J4+J5))+C45(D01(D23(J4+J5)+D34(J3+J4+J5))+D23D34(J1+J2+J3+J4+J5))+D01D23D34D45)+C34(C45(D01(D12(J3+J4+J5)+D23(J2+J3+J4+J5))+D12D23(J1+J2+J3+J4+J5))+D01D12D23D45)+C45D01D12D23D34
a2=C01(C12(C34(D23J5+D45(J3+J4+J5))+C45(D23(J4+J5)+D34(J3+J4+J5))+D23D34D45)+C34(C45(D12(J3+J4+J5)+D23(J2+J3+J4+J5))+D12D23D45)+C45D12D23D34)+C12(C34(C45(D01(J3+J4+J5)+D23(J1+J2+J3+J4+J5))+D01D23D45)+C45D01D23D34)+C34C45D01D12D23
a1=C01(C12(C34(C45(J3+J4+J5)+D23D45)+C45D23D34)+C34C45D12D23)+C12C34C45D01D23
a0=C01C12C34C45D23
b7=D34J1J2J5
b6=(C34J1J2J5+D34(D01J2J5+D12J5(J1+J2)+D45J1J2))
b5=(C01D34J2J5+C12D34J5(J1+J2)+C34(D01J2J5+D12J5(J1+J2)+D45J1J2)+C45D34J1J2+D34(D01(D12J5+D45J2)+D12D45(J1+J2)))
b4=(C01(C34J2J5+D12D34J5+D34D45J2)+C12(C34J5(J1+J2)+D01D34J5+D34D45(J1+J2))+C34(C45J1J2+D01(D12J5+D45J2)+D12D45(J1+J2))+C45D34(D01J2+D12(J1+J2))+D01D12D34D45)
b3=(C01(C12D34J5+C34(D12J5+D45J2)+C45D34J2+D12D34D45)+C12(C34(D01J5+D45(J1+J2))+C45D34(J1+J2)+D01D34D45)+C34(C45(D01J2+D12(J1+J2))+D01D12D45)+C45D01D12D34)
b2=(C01(C12(C34J5+D34D45)+C34(C45J2+D12D45)+C45D12D34)+C12(C34(C45(J1+J2)+D01D45)+C45D01D34)+C34C45D01D12)
b1=(C01(C12(C34D45+C45D34)+C34C45D12)+C12C34C45D01)
b0=C01C12C34C45
Представить передаточную функцию Wp(s) в виде произведения полиномов не выше второго порядка в числителе и знаменателе Wp(s) в аналитическом виде не представляется возможным даже теоретически, т.к. вид корней характеристических полиномов ai,bi, а, следовательно, и вид разложения на полиномы не выше второго порядка, зависит от численных значений параметров элементов модели. Поэтому исследование влияния элементов модели на устойчивость ГС проводилось численно, путем нахождения корней характеристических полиномов для каждого частного случая. Далее по полученным корням определялись полиномы не выше второго порядка по которым и строилась ЛАХ разомкнутой системы.
Все математические операции проводилось с использованием пакета “MATHCAD” с помощью которого численно определялись корни полиномов в передаточной функции разомкнутой системы Wp(s), зная которые можно представить Wp(s) в виде последовательного соединения элементарных звеньев. Это выполняется следующим образом. Пусть полиномы числителя и знаменателя Wp(s) имеют корни lai, lbi соответственно. Эти корни могут быть нулевыми, действительными и комплексно сопряженными. Каждый нулевой корень знаменателя lai=0 обеспечивает появление в составе Wp(s) интегрирующего звена Wi(s)= 1/s, соответственно lbi=0 отвечает за появление чисто дифференцирующего звена с Wi(s)= s. Каждый из действительных корней lai, lbi приносит в числитель или знаменатель соответственно выражение вида (TiЧs+1)Ч(1/Ti), где Ti=1/li , что соответствует появлению апериодических и дифференцирующих звеньев в составе Wp(s). Каждая пара комплексно сопряженных корней li, li* в составе числителя или знаменателя передаточной функции отвечает за появление в числителе или знаменателе соответственно выражений вида (Ti2 Ч s2 +2ЧxiЧTiЧs +1)Ч(1/Ti2), где Ti=1 / |li| , xi=Re(li) / |li|. Таким образом, зная корни полиномов числителя и знаменателя передаточной функции можно представить её в виде:
П(si)ЧП(TgЧs+1)ЧП( Tn2 Ч s2 +2ЧxnЧTnЧs +1)
![]() Wp(s)
= k Ч
kw Ч (9)
Wp(s)
= k Ч
kw Ч (9)
П(sj)ЧП(TkЧs+1)ЧП( Tm2 Ч s2 +2ЧxmЧTmЧs +1)
П(1/Ti) Ч П(1/Ti2)
![]() где
kw =
где
kw =
П(1/Ti) Ч П(1/Ti2)
Для численных расчетов примем базовые параметры модели характерными для ГС данного типа, которые равны следующим значениям:
J1 = 0.25 кгЧм2 C01 = 1Ч103 НЧм/рад. D01=0.001 НЧмЧс
J2 = 0.03 кгЧм2 C12 = 1Ч103 НЧм/рад. D12=0.001 НЧмЧс
J3 = 0.01 кгЧм2 C23 = 0 D23=0.1 НЧмЧс
J4 = 0.15 кгЧм2 C34 =1Ч104 НЧм/рад. D34=0.001 НЧмЧс
J5 = 1 кгЧм2 C45 =1Ч103 НЧм/рад. D45=0.01 НЧмЧс
К = 1000
Рассмотрим следующие варианты модели:
1) ГС с “жесткими” рамами и редуктором.
Начальные параметры модели принимают следующие знечения:
J1 = 0.25 кгЧм2 C01 = 1Ч1020 НЧм/рад. D01= 0.001 НЧмЧс
J2 = 0.03 кгЧм2 C12 = 1Ч1020 НЧм/рад. D12= 0.001 НЧмЧс
J3 = 0.01 кгЧм2 C23 = 0 D23=0.1 НЧмЧс
J4 = 0.15 кгЧм2 C34 =1Ч1020 НЧм/рад. D34=0.001 НЧмЧс
J5 = 1 кгЧм2 C45 =1Ч1020 НЧм/рад. D45=0.01 НЧмЧс
К = 1000
Варьируем D23 = 0.01 ... 1 HЧмЧс
Передаточная функция при этом имеет вид:
k Ч kw
![]() Wp(s)= (10)
Wp(s)= (10)
s Ч (TЧs+1)
Значения постоянной времени Т, w, kw приведены в Табл.1.
Табл.1.
| D23 | T | w=1/T | kw |
| 0.01 | 116 | 0.0086 | 150 |
| 0.1 | 11.6 | 0.086 | 15 |
| 1 | 1.16 | 0.86 | 1.5 |
| 10 | 0.116 | 8.6 | 0.15 |
Т.о. ЛАХ модели с бесконечно жесткими пружинами соответствует ЛАХ идеализированного индикаторного ГС. Постоянная времени Т апериодического звена апроксимируется формулой:
J3 +J4 +J5
![]() Т= (11)
Т= (11)
D23
2) ГС с “нежестким” редуктором.
Начальные параметры модели:
J1 = 0.25 кгЧм2 C01 = 1Ч1020 НЧм/рад. D01= 0.001 НЧмЧс
J2 = 0.03 кгЧм2 C12 = 1Ч1020 НЧм/рад. D12= 0.001 НЧмЧс
J3 = 0.01 кгЧм2 C23 = 0 D23=0.1 НЧмЧс
J4 = 0.15 кгЧм2 C34 =1Ч104 НЧм/рад. D34=0.001 НЧмЧс
J5 = 1 кгЧм2 C45 =1Ч1020 НЧм/рад. D45=0.01 НЧмЧс
К = 1000
Варьируем нежесткость редуктора С34=103 ... 107 HЧм/рад.
Передаточная функция при этом имеет вид:
k Ч kw
![]() Wp(s)= (12)
Wp(s)= (12)
s Ч (T1Чs+1)Ч( T22 Ч s2 +2Чx2ЧT2Чs +1)
Значения постоянных времени Т1, Т2, соответствующие им частоты “излома” ЛАХ w1, w1, удельный коэффициент демпфирования x2 и коэффициент передачи модели kw приведены в Табл.2. и Табл.3.
Табл.2.
| C34 | T1 | w1 | T2 | w2 | x2 | kw |
| 103 | 24.25 | 0.04 | 0.0031 | 323 | 0.016 | 31.36 |
| 104 | 24.25 | 0.04 | 0.001 | 103 | 0.005 | 31.36 |
| 105 | 24.25 | 0.04 | 3.1Ч10-4 | 3.23 | 0.0016 | 31.36 |
| 106 | 24.25 | 0.04 | 1Ч10-4 | 104 | 0.0005 | 31.36 |
Как видно из Табл.2. нежесткость редуктора влияет только на расположение колебательного звена на оси частот (Т2, w2) и коэффициент демпфирования в этом звене (x2).
Влияние демпфирования в редукторе на поведение ЛАХ определяем варьируя D34=0.001 ... 0.1 НЧмЧс (при С34=104 = const.).
Табл.3.
| D34 | T1 | w1 | T2 | w2 | x2 | kw |
| 0.0001 | 25.9 | 0.039 | 0.001 | 103 | 0.0049 | 334.8 |
| 0.001 | 24.25 | 0.04 | 0.001 | 103 | 0.005 | 31.36 |
| 0.01 | 14.86 | 0.067 | 0.001 | 103 | 0.0054 | 1.92 |
| 0.1 | 11.6 | 0.086 | 0.001 | 103 | 0.01 | 0.15 |
Как видно из Табл.3., изменение демпфирования в редукторе влияет не только на коэффициент демпфирования в колебательном звене, но и на расположение на оси частот апериодического звена (Т1), и на коэффициент передачи модели.
3) ГС с “нежесткой” связью платформы со стабилизируемым объектом (телекамерой).
Исходные параметры модели:
J1 = 0.25 кгЧм2 C01 = 1Ч1020 НЧм/рад. D01= 0.001 НЧмЧс
J2 = 0.03 кгЧм2 C12 = 1Ч1020 НЧм/рад. D12= 0.001 НЧмЧс
J3 = 0.01 кгЧм2 C23 = 0 D23=0.1 НЧмЧс
J4 = 0.15 кгЧм2 C34 =1Ч1020 НЧм/рад. D34=0.001 НЧмЧс
J5 = 1 кгЧм2 C45 =1Ч103 НЧм/рад. D45=0.01 НЧмЧс
К = 1000
Варьируем С45 = 102 ... 106 HЧм/рад.
Передаточная функция при этом имеет вид:
k Ч kwЧ( T32 Ч s2 +2Чx3ЧT3Чs +1)
![]() Wp(s)= (13)
Wp(s)= (13)
s Ч (T1Чs+1)Ч( T22 Ч s2 +2Чx2ЧT2Чs +1)
Влияние жесткости крепления стабилизируемого объекта к платформе на передаточную функцию Wp(s) приведено в Табл.4.
Табл.4.
| C45 | T1 (w1) | T2 (w2) | x2 | T3 (w3) | x3 | kw |
| 102 | 11.6 (0.086) | 0.037(27) | 0.011 | 0.1 (10) | 5Ч10-4 | 15 |
| 103 | 11.6 (0.086) | 0.012(85) | 0.0036 | 0.032(31.3) | 1.6Ч10-4 | 15 |
| 104 | 11.6 (0.086) | 0.0037(270) | 0.0011 | 0.01(100) | 5Ч10-5 | 15 |
| 105 | 11.6 (0.086) | 1.2Ч10-3(850) | 0.00036 | 3.2Ч10-3(313) | 1.6Ч10-5 | 15 |
Влияние демпфирования в креплении стабилизируемого объекта к платформе на передаточную функцию Wp(s) приведено в Табл.5. Коэффициент демпфирования изменяется в пределах D45=0.001 ... 0.1 НЧмЧс, при постоянной жесткости крепления объекта к платформе равной C45=1000 HЧм/рад =const.
Табл.5.
| D45 | T1 (w1) | T2 (w2) | x2 | T3 (w3) | x3 | kw |
| 0.001 | 11.6 (0.086) | 0.012(85) | 0.0032 | 0.032 (31.3) | 2.7Ч10-14 | 15 |
| 0.01 | 11.6 (0.086) | 0.012(85) | 0.0036 | 0.032(31.3) | 1.6Ч10-4 | 15 |
| 0.1 | 11.6 (0.086) | 0.012(85) | 0.0074 | 0.032(31.3) | 1.6Ч10-3 | 15 |
Как видно из Табл.4. и 5., нежесткость крепления объекта к платформе вызывает появление в составе ЛАХ двух звеньев: колебательного и антиколебательного, причем антиколебательное звено всегда расположено в области более низких частот, чем колебательное. Это влечет появление в ЛАХ участка с наклоном в 0 Дб/дек., который в случае его расположения до частоты среза, увеличивает частоту среза, что вызывает трудности в технической реализации такой системы стабилизации. Демпфирование в креплении объекта к платформе влияет только на удельные коэффициенты демпфирования x2, x3 в колебательном и антиколебательном звеньях, причем особенно сильно изменяется x3.
4) ГС с “нежестким” креплением статора двигателя стабилизации к наружной раме (задняя нежесткость).
Параметры модели:
J1 = 0.25 кгЧм2 C01 = 1Ч1020 НЧм/рад. D01= 0.001 НЧмЧс
J2 = 0.03 кгЧм2 C12 = 1Ч103 НЧм/рад. D12= 0.001 НЧмЧс
J3 = 0.01 кгЧм2 C23 = 0 D23=0.1 НЧмЧс
J4 = 0.15 кгЧм2 C34 =1Ч1020 НЧм/рад. D34=0.001 НЧмЧс
J5 = 1 кгЧм2 C45 =1Ч1020 НЧм/рад. D45=0.01 НЧмЧс
К = 1000
Варьируем С12 = 102 ... 106 HЧм/рад.
Передаточная функция при этом имеет вид:
k Ч kwЧ( T32 Ч s2 +2Чx3ЧT3Чs +1)
![]() Wp(s)= (14)
Wp(s)= (14)
s Ч (T1Чs+1)Ч( T22 Ч s2 +2Чx2ЧT2Чs +1)
Варьируем С12 (при D12=0.001 НЧмЧс=const), результаты приведены в Табл.6.
Табл.6.
| C12 | T1 | T2 | x2 | T3 | x3 | kw |
| 102 | 11.6 | 0.017 | 0.03 | 0.017 | 0.0003 | 15 |
| 103 | 11.6 | 0.0055 | 0.0092 | 0.0055 | 9.1Ч10-5 | 15 |
| 104 | 11.6 | 0.0017 | 0.003 | 0.0017 | 2.9Ч10-5 | 15 |
| 105 | 11.6 | 0.00055 | .00092 | .00055 | 9.1Ч10-6 | 15 |
Варьируем D12 (при С12=1000 HЧм/рад = const.), результаты приведены в Табл.7.
Табл.7.
| D12 | T1/w1 | T2 / w2 | x2 | T3 / w3 | x3 | kw |
| 10-4 | 11.6 | 0.0055 | 0.0092 | 0.0055 | 8.3Ч10-14 | 15 |
| 10-3 | 11.6 | 0.0055 | 0.0092 | 0.0055 | 9.1Ч10-5 | 15 |
| 10-2 | 11.6 | 0.0055 | 0.01 | 0.0055 | 0.00091 | 15 |
Как видно из Табл.6, нежесткость крепления статора двигателя стабилизации к основанию, приводит к появлению в составе передаточной функции Wp(s) колебательного и антиколебательного звеньев с одинаковыми постоянными времени и различными коэффициентами демпфирования. Т.к. постоянные времени этих звеньев одинаковы, то наличие “задней” нежесткости никак не отражается на виде ЛАХ, однако различия этих звеньев в коэффициентах демпфирования влекут разную скорость “переключения” фазы в каждом звене, что вызывает появление незначительных по амплитуде выбросов на фазо-частотной характеристике.
5) ГС с “нежесткой” наружной рамкой.
Исходные параметры модели:
J1 = 0.25 кгЧм2 C01 = 1Ч103 НЧм/рад. D01= 0.001 НЧмЧс
J2 = 0.03 кгЧм2 C12 = 1Ч103 НЧм/рад. D12= 0.001 НЧмЧс
J3 = 0.01 кгЧм2 C23 = 0 D23=0.1 НЧмЧс
J4 = 0.15 кгЧм2 C34 =1Ч1020 НЧм/рад. D34=0.001 НЧмЧс
J5 = 1 кгЧм2 C45 =1Ч1020 НЧм/рад. D45=0.01 НЧмЧс
К = 1000
Варьируем С01,С12 = 102 ... 106 HЧм/рад.
Передаточная функция при этом имеет вид:
k Ч kwЧ( T42 Ч s2 +2Чx4ЧT4Чs +1) Ч( T52 Ч s2 +2Чx5ЧT5Чs +1)
![]() Wp(s)= (14)
Wp(s)= (14)
s Ч (T1Чs+1)Ч( T22 Ч s2 +2Чx2ЧT2Чs +1) Ч( T32 Ч s2 +2Чx3ЧT3Чs +1)
Вначале варьируем С01, при С12=const., результаты приведены в Табл.8.
Табл.8.
| C01 | T1 | T2 | x2 | T3 | x3 | T4 | x4 | T5 | x5 | kw |
| 102 | 11.6 | 0.0052 | 0.0078 | 0.053 | 0.0097 | 0.0052 | 0.0001 | 0.053 | 1.8 10-13 | 15 |
| 103 | 11.6 | 0.0051 | 0.0076 | 0.017 | 0.0037 | 0.0051 | 9.7 10-5 | 0.017 | 1.76 10-13 | 15 |
| 104 | 11.6 | 0.0062 | 0.0074 | 0.0044 | 0.0022 | 0.0044 | 5.7 10-5 | 0.0062 | 4.8 10-5 | 15 |
| 105 | 11.6 | 0.0055 | 0.0093 | 0.0016 | 9.4 10-6 | 0.0055 | 8.9 10-5 | 0.0016 | 4.37 10-13 | 15 |
Далее варьируем С12, при С01=const., результаты - в Табл.9.
Табл.9.
| C12 | T1 | T2 | x2 | T3 | x3 | T4 | x4 | T5 | x5 | kw |
| 102 | 11.6 | 0.0196 | 0.023 | 0.014 | 0.0069 | 0.0196 | 1.5 10-4 | 0.014 | 1.8 10-4 | 15 |
| 104 | 11.6 | 0.0016 | 0.0025 | 0.017 | 0.0031 | 0.0016 | 3.1 10-5 | 0.017 | 1.8 10-13 | 15 |
| 105 | 11.6 | .00052 | .00078 | 0.017 | 0.003 | .00052 | 0.9 10-5 | 0.017 | 1.8 10-13 | 15 |
Варьируя последовательно D01 и D12 выявляем степень их влияния на Ti, при С01=С12=1000 HЧм/рад = const. (Табл.10,11)
Табл.10.
| D01 | T1/w1 | T2 / w2 | x2 | T3 / w3 | x3 | T4 / w4 | x4 | T5 / w5 | x5 | kw |
| 10-4 | 11.6 | 0.0051 | 0.0076 | 0.0168 | 0.0037 | 0.0051 | 9.6Ч10-5 | 0.0168 | 2Ч 10-14 | 15 |
| 10-3 | 11.6 | 0.0051 | 0.0076 | 0.0168 | 0.0037 | 0.0051 | 9.7Ч10-5 | 0.0168 | 17Ч 10-14 | 15 |
| 10-2 | 11.6 | 0.0051 | 0.0076 | 0.0168 | 0.004 | 0.0051 | 11Ч10-5 | 0.0168 | .0003 | 15 |
| 10-1 | 11.6 | 0.0051 | 0.0076 | 0.0168 | 0.007 | 0.0051 | 23Ч10-5 | 0.0168 | .0003 | 15 |
Табл.11.
| D12 | T1/w1 | T2 / w2 | x2 | T3 / w3 | x3 | T4 / w4 | x4 | T5 / w5 | x5 | kw |
| 10-4 | 11.6 | 0.0051 | 0.0075 | 0.0168 | 0.0037 | 0.0051 | 1.1Ч10-5 | 0.0168 | 9Ч 10-6 | 15 |
| 10-2 | 11.6 | 0.0051 | 0.0084 | 0.0168 | 0.0037 | 0.0051 | 9.6Ч10-4 | 0.0168 | 2Ч 10-13 | 15 |
| 10-1 | 11.6 | 0.0051 | 0.017 | 0.0168 | 0.0037 | 0.0051 | 9.6Ч10-3 | 0.0168 | 4.2Ч 10-13 | 15 |
Как видно из таблиц 8 и 9, нежесткая “задняя” рамка (с двумя нежесткостями С01 и С12) приводит к появлению двух пар колебательных и антиколебательных звеньев, имеющих одинаковые постоянные времени, что приводит к их взаимной компенсации и, следовательно, влияние этих звеньев на вид ЛАХ практически отсутствует. Однако на ФЧХ будут присутствовать “выбросы” фазы, причина которых - различия коэффициентов демпфирования в компенсирующих друг друга колебательном и антиколебательном звеньях.
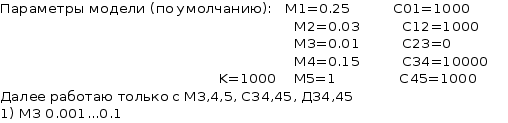
Вид ЛАХ в случае “нежесткой” задней рамки для исходных параметров модели следующий:
![]()

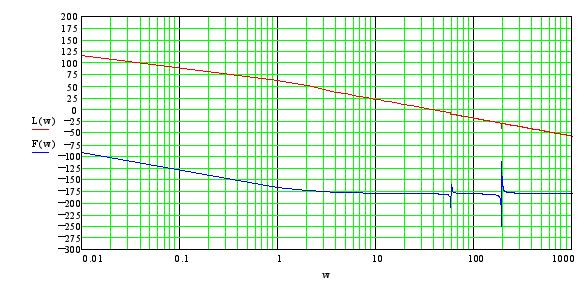
Таким образом, ЛАХ модели с базовыми параметрами:
J1 = 0.25 кгЧм2 C01 = 1Ч103 НЧм/рад. D01= 0.001 НЧмЧс
J2 = 0.03 кгЧм2 C12 = 1Ч103 НЧм/рад. D12= 0.001 НЧмЧс
J3 = 0.01 кгЧм2 C23 = 0 D23=0.1 НЧмЧс
J4 = 0.15 кгЧм2 C34 =1Ч104 НЧм/рад. D34=0.001 НЧмЧс
J5 = 1 кгЧм2 C45 =1Ч103 НЧм/рад. D45=0.01 НЧмЧс
К = 1000
имеет следующий вид.


![]()
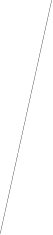
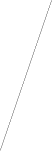
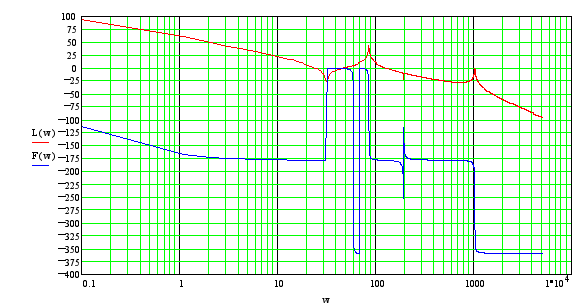
от нежесткости от “задней” от нежесткости
крепления объекта нежесткости редуктора
После предварительного рассмотрения влияния параметров модели на поведение ЛАХ, можно сделать следующие выводы:
1) В практических расчетах каждую нежесткость возможно рассматривать изолировано от других, т.к. при “типовых” параметрах ГС каждая такая нежесткость определяет звенья разнесенные по оси частот на некоторое расстояние и, поэтому, не влияющие друг на друга;
2) Из 1) следует, что влияние нежесткости редуктора на ЛАХ можно проводить основываясь на известных формулах, выведенных для более простой модели ГС, учитывающей только одну нежесткость редуктора;
3) В практических расчетах влиянием “задней” нежесткости можно пренебречь, т.к. она не изменяет вида ЛАХ из-за того, что колебательные и антиколебательные звенья взаимно компенсируют друг друга.
4) Нежесткость крепления объекта стабилизации к платформе вызывает появление на ЛАХ участка на котором характеристика “поднимается” на +40 Дб/дек. из-за появления в передаточной функции колебательного и антиколебательного звеньев, разнесенных по оси частот. Это не влияет на устойчивость системы стабилизации, но затрудняет её техническую реализацию из-за резко возрастающей частоты среза системы.
Таким образом, целесообразно подробнее рассмотреть влияние нежесткости крепления объекта стабилизации к платформе на поведние ЛАХ, при расположении чувствительного элемента на платформе и нежестком редукторе.
Для этого случая базовая модель имеет следующие значения параметров:
J1 = 0.25 кгЧм2 C01 = 1Ч1030 НЧм/рад. D01= 0.001 НЧмЧс
J2 = 0.03 кгЧм2 C12 = 1Ч1030 НЧм/рад. D12= 0.001 НЧмЧс
J3 = 0.01 кгЧм2 C23 = 0 D23=0.1 НЧмЧс
J4 = 0.15 кгЧм2 C34 =1Ч104 НЧм/рад. D34=0.001 НЧмЧс
J5 = 1 кгЧм2 C45 =1Ч103 НЧм/рад. D45=0.01 НЧмЧс
К = 1000
Варьируем следующие переменные: J3, J4, J5, C34, C45, D34, D45, при фиксированых значениях остальных параметров, равных базовым. Все единицы в СИ.
Передаточная функция для данной модели имеет вид:
k Ч kwЧ( T42 Ч s2 +2Чx4ЧT4Чs +1)
![]() Wp(s)= (15)
Wp(s)= (15)
s Ч (T1Чs+1)Ч( T22 Ч s2 +2Чx2ЧT2Чs +1) Ч( T32 Ч s2 +2Чx3ЧT3Чs +1)
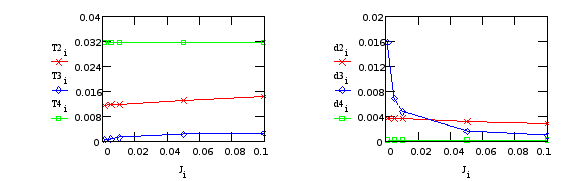
1) Влияние изменений моментов инерции тел.
a) Варьируем J3 (момент инерции ротора двигателя стабилизации):
Табл.12.
| J3 | T1 | T2 | T3 | x2 | x3 | T4 | x4 | kw |
| 0.001 | 11.51 | 0.01145 | 0.000315 | 0.003737 | 0.015813 | 0.031623 | 0.000158 | 1.5 |
| 0.005 | 11.55 | 0.01159 | 0.000700 | 0.003691 | 0.006803 | 0.031623 | 0.000158 | 7.5 |
| 0.01 | 11.60 | 0.01175 | 0.000970 | 0.003634 | 0.004588 | 0.031623 | 0.000158 | 15 |
| 0.05 | 12.00 | 0.01295 | 0.001930 | 0.003206 | 0.001472 | 0.031623 | 0.000158 | 75 |
| 0.1 | 12.50 | 0.01426 | 0.002430 | 0.002766 | 0.000760 | 0.031623 | 0.000158 | 150 |
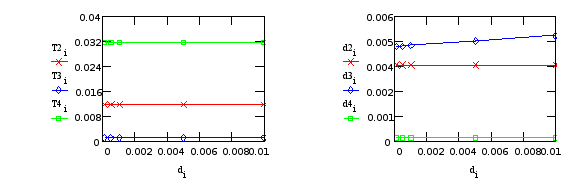
Характер изменения постоянных времени колебательных звеньев Т2, Т3, Т4 и коэффициента демпфирования в этих звеньях, представлен на графиках (Т3, d3 относятся к редуктору; T2, T4, d2, d4 - к креплению телекамеры):
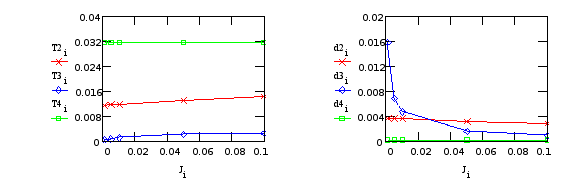
б) Варьируем J4 (момент инерции платформы):
Табл.13.
| J4 | T1 | T2 | T3 | x2 | x3 | T4 | x4 | kw |
| 0.015 | 10.24990 | 0.004979 | 0.000768 | 0.011187 | 0.002402 | 0.031623 | 0.000158 | 1.5 |
| 0.075 | 10.84991 | 0.008857 | 0.000939 | 0.005476 | 0.004190 | 0.031623 | 0.000158 | 7.5 |
| 0.15 | 11.59992 | 0.011747 | 0.000968 | 0.003633 | 0.004588 | 0.031623 | 0.000158 | 15 |
| 0.75 | 17.59996 | 0.020780 | 0.000993 | 0.001021 | 0.004952 | 0.031623 | 0.000158 | 75 |
| 1.5 | 25.09997 | 0.024527 | 0.000997 | 0.000529 | 0.005001 | 0.031623 | 0.000158 | 150 |
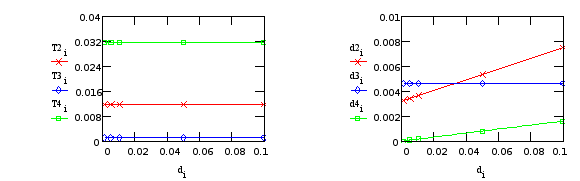
Т3, d3 - от “редуктора”; T2, T4, d2, d4 - от крепления телекамеры.
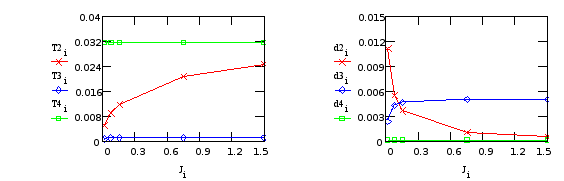
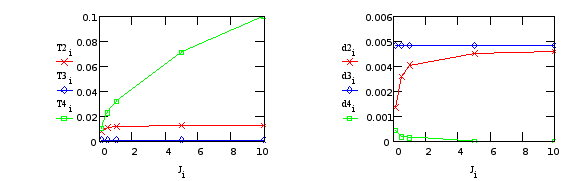
в) Варьируем J5 (момент инерции телекамеры):
Табл.14.
| J5 | T1 | T2 | T3 | x2 | x3 | T4 | x4 | kw |
| 0.1 | 2.599976 | 0.007846 | 0.000968 | 0.001609 | 0.004588 | 0.01 | 0.0005 | 15.00000 |
| 0.5 | 6.599933 | 0.011012 | 0.000968 | 0.003102 | 0.004588 | 0.022361 | 0.000224 | 15.00000 |
| 1 | 11.59992 | 0.011747 | 0.000968 | 0.003634 | 0.004588 | 0.031623 | 0.000158 | 15.00000 |
| 5 | 51.59989 | 0.012454 | 0.000968 | 0.004219 | 0.004588 | 0.070711 | 0.000000 | 15.00000 |
| 10 | 101.5999 | 0.012552 | 0.000968 | 0.004305 | 0.004588 | 0.1 | 0.000000 | 14.99999 |
Т3, d3 - от “редуктора”; T2, T4, d2, d4 - от крепления телекамеры.
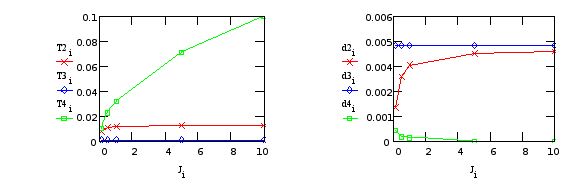
Из Табл.12...14 видно, что моменты инерции каждого из элементов модели сильно влияют только на одну из постоянных времени мало изменяя другие, поэтому в практических расчетах их можно считать независимыми.
2) Влияние нежесткостей редуктора С34 и крепления телекамеры к платформе С45.
а) Варьируем C34 (нежесткость редуктора):
Табл.15.
| C34 | T1 | T2 | T3 | x2 | x3 | T4 | x4 | kw |
| 100 | 11.59894 | 0.012303 | 0.009243 | 0.020021 | 0.031623 | 0.031623 | 0.000158 | 15.00000 |
| 500 | 11.59973 | 0.011797 | 0.004311 | 0.004659 | 0.020062 | 0.031623 | 0.000158 | 15.00000 |
| 1000 | 11.59983 | 0.011769 | 0.003056 | 0.004070 | 0.014370 | 0.031623 | 0.000158 | 15.00000 |
| 5000 | 11.59991 | 0.011749 | 0.001367 | 0.003678 | 0.006482 | 0.031623 | 0.000158 | 15.00000 |
| 10000 | 11.59992 | 0.011747 | 0.000968 | 0.003634 | 0.004588 | 0.031623 | 0.000158 | 15.00000 |
| 50000 | 11.59992 | 0.011745 | 0.000433 | 0.003598 | 0.002053 | 0.031623 | 0.000158 | 15.00000 |
| 100000 | 11.59993 | 0.011745 | 0.000306 | 0.003594 | 0.001452 | 0.031623 | 0.000158 | 15.00000 |
Т3, d3 - от “редуктора”; T2, T4, d2, d4 - от крепления телекамеры.
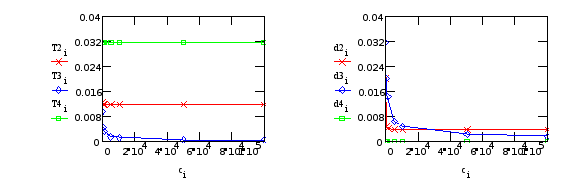
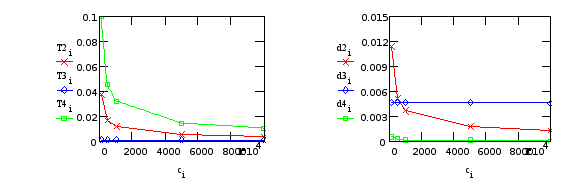
б) Варьируем C45 (нежесткость крепления телекамеры):
Табл.16.
| C45 | T1 | T2 | T3 | x2 | x3 | T4 | x4 | kw |
| 100 | 11.59925 | 0.037141 | 0.000968 | 0.011366 | 0.004592 | 0.1 | 0.0005 | 15.00000 |
| 500 | 11.59984 | 0.016611 | 0.000968 | 0.005107 | 0.004590 | 0.044721 | 0.000224 | 15.00000 |
| 1000 | 11.59992 | 0.011747 | 0.000968 | 0.003634 | 0.004588 | 0.031623 | 0.000158 | 15.00000 |
| 5000 | 11.59998 | 0.005258 | 0.000967 | 0.001707 | 0.004569 | 0.014142 | 0.000071 | 15.00000 |
| 10000 | 11.59998 | 0.003722 | 0.000966 | 0.001287 | 0.004544 | 0.001 | 0.000050 | 15.00000 |
Т3, d3 - от “редуктора”; T2, T4, d2, d4 - от крепления телекамеры.
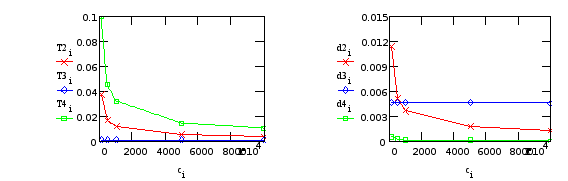
Из Табл.15,16 видно, что изменение нежесткости редуктора сильно меняет параметры только одного колебательного звена, появление которого вызвано нежесткостью редуктора, при этом параметры других звеньев практически не изменяются. Аналогично, нежесткость крепления телекамеры практически не влияет на колебательное звено появление которого вызывается нежесткостью редуктора. Это подтверждает вывод о том, что “колебательности” редуктора и крепления телекамеры можно рассматривать независимо.
3) Влияние демпфирования в редукторе D34 и элементах крепления телекамеры D45.
а) Варьируем D34 (редуктор):
Табл.17.
| D34 | T1 | T2 | T3 | x2 | x3 | T4 | x4 | kw |
| 0.0001 | 11.59992 | 0.011747 | 0.000968 | 0.003624 | 0.004541 | 0.031623 | 0.000158 | 150 |
| 0.0005 | 11.59992 | 0.011747 | 0.000968 | 0.003624 | 0.004562 | 0.031623 | 0.000158 | 30 |
| 0.001 | 11.59992 | 0.011747 | 0.000968 | 0.003624 | 0.004588 | 0.031623 | 0.000158 | 15 |
| 0.005 | 11.59992 | 0.011747 | 0.000968 | 0.003624 | 0.004794 | 0.031623 | 0.000158 | 3 |
| 0.01 | 11.59992 | 0.011747 | 0.000968 | 0.003624 | 0.005053 | 0.031623 | 0.000158 | 1.5 |
Т3, d3 - от “редуктора”; T2, T4, d2, d4 - от крепления телекамеры.
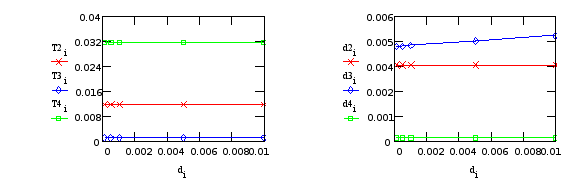
б) Варьируем D45 (крепление телекамеры):
Табл.18.
| D45 | T1 | T2 | T3 | x2 | x3 | T4 | x4 | kw |
| 0.001 | 11.59992 | 0.011747 | 0.000968 | 0.003251 | 0.004586 | 0.031623 | 2.66Ч10-19 | 15.00000 |
| 0.005 | 11.59992 | 0.011747 | 0.000968 | 0.003421 | 0.004587 | 0.031623 | 0.000079 | 15.00000 |
| 0.01 | 11.59992 | 0.011747 | 0.000968 | 0.003634 | 0.004588 | 0.031623 | 0.000158 | 15.00000 |
| 0.05 | 11.59992 | 0.011747 | 0.000968 | 0.005335 | 0.004596 | 0.031623 | 0.000791 | 15.00000 |
| 0.1 | 11.59992 | 0.011747 | 0.000968 | 0.007463 | 0.004606 | 0.031623 | 0.001581 | 15.00000 |
Т3, d3 - от “редуктора”; T2, T4, d2, d4 - от крепления телекамеры.
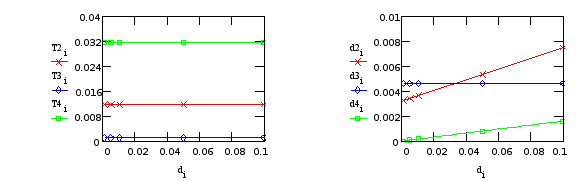
Из Табл.17,18 видно, что вариации коэффициента демпфирования в редукторе и креплении телекамеры не влияют на постоянные времени звеньев и, кроме того демпфирование в редукторе не влияет на коэффициенты демпфирования в колебательных звеньях, вызываемых нежестким креплением телекамеры, и, наоборот, изменение демпфирования в креплении телекамеры не влияет на коэффициент демпфирования в колебательном звене “от редуктора”.
Таким образом, можно сделать вывод, что в практических расчетах влияние нежесткостей редуктора и крепления телекамеры можно рассматривать независимо друг от друга.
Для частного случая, учитывающего только влияние нежесткости крепления объекта стабилизации к платформе на ЛАХ, возможно получение выражения для передаточной функции в символьном виде.
Для этого рассмотрим модель с “жестким” редуктором, т.е. полагая, что С34 бесконечно велико, и не учитывая нежесткость наружной рамы. Тогда базовая модель будет включать в себя только следующие элементы:
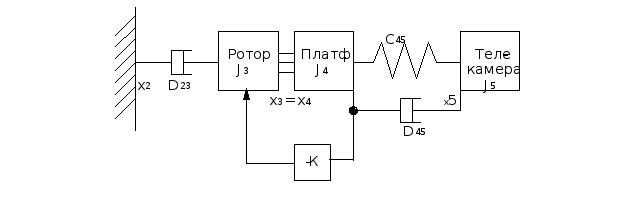
Рис.2.
J3 = 0.01 кгЧм2 - ротор;
J4 = 0.15 кгЧм2 -платформа;
J5 = 1 кгЧм2 - телекамера;
C45 =1Ч103 НЧм/рад. - нежесткость крепления телекамеры;
D23=0.1 НЧмЧс - демпфирование в двигателе стабилизации;
D45=0.01 НЧмЧс - демпфирование в креплении телекамеры;
К = 1000 - коэффициент передачи цепи обратной
связи.
В этом случае уравнения движения модели (1) с учетом того, что x3=x4 имеют следующий вид:
(J3+J4)Чx4''+D23Чx4'-D45Ч(x5'-x4')-C45Ч(x5-x4)=-KЧx4 (16)
J5Чx5''+D45Ч(x5'-x4')+C45Ч(x5-x4) = 0
Переписав в операторной форме и преобразовав, получим:
((J3+J4)Чs2+D23Чs +D45Чs+C45)Чx4-(D45Чs+C45)Чx5=-KЧx4 (17)
(J5Чs2+D45Чs+C45)Чx5-(D45Чs+C45)Чx4=0
Для нахождения передаточной функции разомкнутой системы по управляющему воздействию Wp(s) составим два определителя: главный - D, и характеризующий входное воздействие D1.
![]()
![]()
((J3+J4)Чs2+D23Чs +D45Чs+C45) -(D45Чs+C45)
D = (18)
-(D45Чs+C45) (J5Чs2+D45Чs+C45)
![]()
![]() -KЧx4 -(D45Чs+C45)
-KЧx4 -(D45Чs+C45)
D1 = (19)
0 (J5Чs2+D45Чs+C45)
Передаточная функция разомкнутой системы определяется как:
D1
![]() Wp(s)
= = (20)
Wp(s)
= = (20)
DЧx4
-KЧ(J5Чs2+D45Чs+C45)
![]() =
=
J5Ч(J3+J4)Чs4+(D23ЧJ5+D45Ч(J3+J4+J5))Чs3+(C45Ч(J3+J4+J5)+D23ЧD45)Чs2+C45ЧD23Чs
Пусть передаточная функция Wp(s) представляется в виде следующего выражения:
-KpЧ( T12 Ч s2 +2Чx1ЧT1Чs +1)
![]() Wp(s)= (21)
Wp(s)= (21)
s Ч (T3Чs+1)Ч( T22 Ч s2 +2Чx2ЧT2Чs +1)
Раскрывая скобки в (21), получаем:
-KpЧ( T12 Ч s2 +2Чx1ЧT1Чs +1)
![]() Wp(s)= (22)
Wp(s)= (22)
T22ЧT3Чs4+(T22+2Чx2ЧT2ЧT3)Чs3+(2Чx2ЧT2+T3)Чs2+s
Приравнивая члены при одинаковых степенях s в выражениях (20) и (22), получаем следующую систему уравнений:
T22ЧT3 = J5Ч(J3+J4)/(C45ЧD23)
T22+2Чx2ЧT2ЧT3 = (D23ЧJ5+D45Ч(J3+J4+J5))/(C45ЧD23) (23)
2Чx2ЧT2+T3 = ((J3+J4+J5)ЧC45+D23ЧD45)/(C45ЧD23)
Kp = K/D23
Решая систему уравнений (23), определим постоянные времени звеньев входящих в передаточную функцию Wp(s) (21):
J5
![]() T1
=
T1
=
C45
 J5Ч(J3+J4)
J5Ч(J3+J4)
![]() T2
= (24)
T2
= (24)
(J3+J4+J5)ЧC45+D23ЧD45
J3+J4+J5 D45
![]()
![]() T3
= Ч
T3
= Ч
D23 C45
Расчет постоянных времени передаточной функции проведенный по формулам (24) дает результат совпадающий с расчетом выполненныи с помощью численных методов.
Выводы сделаные ранее возможно представить в более общем виде. Модель приведенную на Рис.1 можно обобщить, представив ее в виде нескольких упруго-массовых элементов, соединенных последовательно и охваченных цепью обратной связи. Вид такой модели приведен на Рис.3.
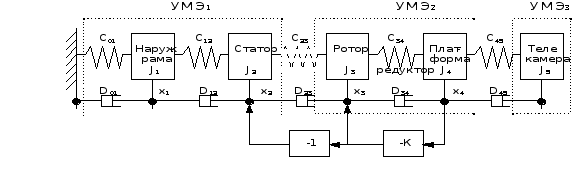
Рис. 3.
здесь УМЭ - упруго-массовый элемент.
Выводы:
1) Каждая колебательная система (Cij-Dij-Jj) в УМЭ1 (т.е. “слева” от контура стабилизации) приводит к появлению в передаточной функции разомкнутой системы Wp(s) пары из колебательного и антиколебательного звеньев имеющих одинаковые постоянные времени. Эти звенья взаимно компенсируют друг друга и, поэтому влияния на поведение ЛАХ практически не оказывют, однако из-за различия в коэффициентах демпфирования в этих звеньях, возникают выбросы на фазочастотной характеристике.
2) Колебательные системы в УМЭ2, (т.е. “внутри” контура стабилизации) вызывают появление в Wp(s) колебательных звеньев.
3) Колебательные системы в УМЭ3, т.е. находящиеся “за” чувствительным элементом, вызывают появление в Wp(s) пары из колебательного и антиколебательного звеньев постоянные времени которых, однако, не совпадают, причем антиколебательное звено всегда расположено на оси частот левее, чем колебательное, поэтому всегда имеет место местный “подъем” ЛАХ на +40 Дб/дек.
Программа построения ЛАХ непосредственным образом, без разложения на элементарные звенья.

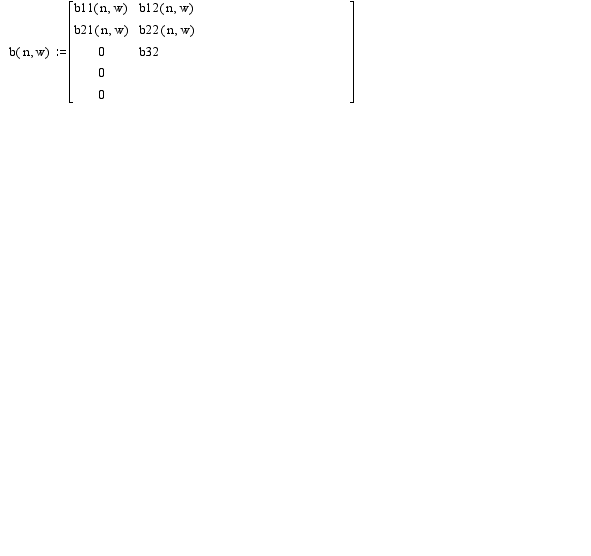
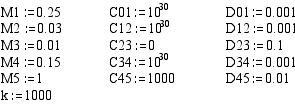
Вычисляю корни полиномов ai , b1 передаточной функции:
W(s) = (1/s)*(-K)*((b7*s7+b6*s6 + ... +b0)/(a9*s9 + a8*s8 + ... + a0))
Ввод 0,1,2....9
aa0:=........
aa1:=........
aa2:=........
aa3:=........
aa4:=........
aa5:=........
aa6:=........
aa7:=........
aa8:=........ (....... - выражения для aai, bbi см. записку)
aa9:=........
bb0:=........
bb1:=........
bb2:=........
bb3:=........
bb4:=........
bb5:=........
bb6:=........
bb7:=........

Определяю постоянные времени Тi (проверяй отрицательность действительной части).
Корни полиномов А и В следующие.
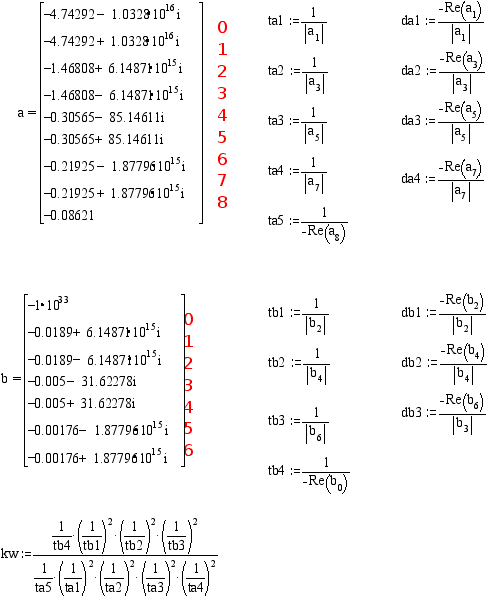
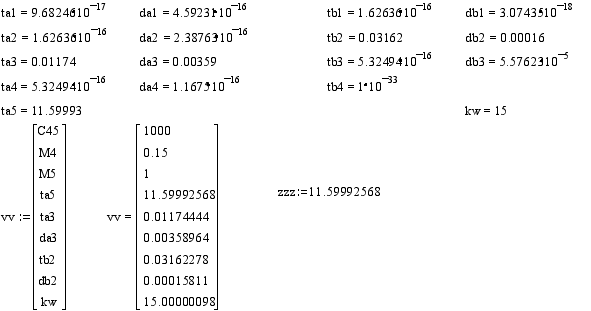
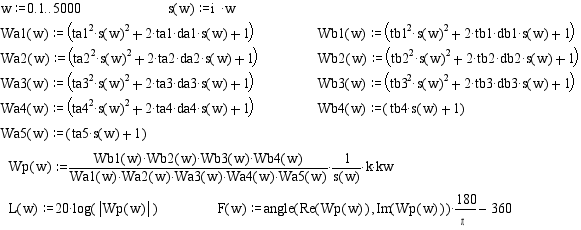
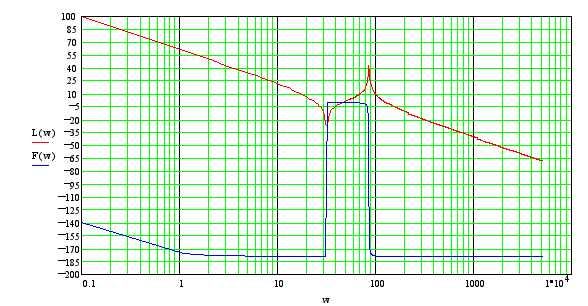
Программа вывода графических зависимостей для переменных входящих в состав передаточной функции.


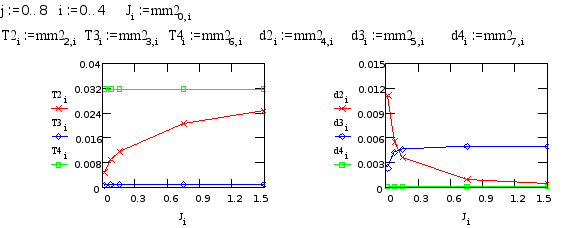
![]()

![]()
![]()
сс34:=

![]()
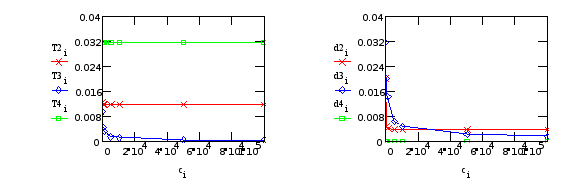
![]()

![]()
![]()

![]()
![]()

![]()
; Рабочая программа для пакета "DERIVE" для случая 1) - неподвижного основания.
; Входные данные.
; Условия неподвижности основания.
WX0:=0
WY0:=0
WZ0:=0
WX01:=0
WY01:=0
WZ01:=0
IYX1:=ixy1
IYX2:=ixy2
IZX1:=ixz1
IZX2:=ixz2
IZY1:=iyz1
IZY2:=iyz2
; Выражения для угловых скоростей.
WX1:=WX0 * COS(alfa) - WZ0 * SIN(alfa)
WY1:=WX1 * TAN(beta) + wy2 / COS(beta)
WZ1:=WX0 * SIN(alfa) + WZ0 * COS(alfa)
WX11:=WX01 * COS(alfa) - WZ01 * SIN(alfa)
WY11:=WX11 * TAN(beta) + wy21 / COS(beta)
WZ11:=WX01 * SIN(alfa) + WZ01 * COS(alfa)
WX2:=WX1 * COS(beta) + WY1 * SIN(beta)
WX21:=WX11 * COS(beta) + WY11 * SIN(beta)
; Выражения для моментов количества движения.
QX1:=ix1 * WX1 - ixy1 * WY1 - ixz1 * WZ1
QY1:=iy1 * WY1 - IYX1 * WX1 - iyz1 * WZ1
QZ1:=iz1 * WZ1 - IZX1 * WX1 - IZY1 * WY1
QX2:=ix2 * WX2 - ixy2 * wy2 - ixz2 * wz2
QY2:=iy2 * wy2 - IYX2 * WX2 - iyz2 * wz2
QZ2:=iz2 * wz2 - IZX2 * WX2 - IZY2 * wy2
QY11:=iy1 * WY11 - IYX1 * WX11 - iyz1 * WZ11
QX21:=ix2 * WX21 - ixy2 * wy21 - ixz2 * wz21
QY21:=iy2 * wy21 - IYX2 * WX21 - iyz2 * wz21
QZ21:=iz2 * wz21 - IZX2 * WX21 - IZY2 * wy21
; Выражения для возмущающих моментов.
MY1:=QY11 - QZ1 * WX1 + QX1 * WZ1
MX2:=QX21 - QY2 * wz2 + QZ2 * wy2
MY2:=QY21 - QZ2 * WX2 + QX2 * wz2
MZ2:=QZ21 - QX2 * wy2 + QY2 * WX2
MY1IN:=MY1 + MX2 * SIN(beta) + MY2 * COS(beta)
; Блок решения.
; Упрощение выражения для Mz2.
MZ2:= - ix2 * wy2^2 * TAN(beta) - ixz2 * wy21 * TAN(beta) + iy2 * wy2^2 * TAN(beta) - iyz2 * wy2 * wz2 * TAN(beta) - ixy2 * wy2^2 * TAN(beta)^2 + ixy2 * wy2^2 + ixz2 * wy2 * wz2 - iyz2 * wy21 + iz2 * wz21
; Упрощение выражения для My1.
MY1IN:= - ixy2 * wy2 * wz2 * COS(beta) - ixz2 * wz2^2 * COS(beta) + iy2 * wy21 * COS(beta) - iyz2 * wz21 * COS(beta) + ix2 * wy21 * SIN(beta)^2 / COS(beta) + ixy2 * wy2 * wz2 * SIN(beta)^2 / COS(beta) + iy1 * wy21 / COS(beta) + ix2 * wy2 * wz2 * SIN(beta) - 2 * ixy2 * wy21 * SIN(beta) - ixz2 * wz21 * SIN(beta) - iy2 * wy2 * wz2 * SIN(beta) + iyz2 * wz2^2 * SIN(beta)
; Рабочая программа для пакета "DERIVE" для случая 2) - неподвижной платформы.
; Входные данные.
; Условия неподвижности платформы.
WY2:=0
WY21:=0
WZ2:=0
WZ21:=0
IYX1:=ixy1
IYX2:=ixy2
IZX1:=ixz1
IZX2:=ixz2
IZY1:=iyz1
IZY2:=iyz2
; Выражения для угловых скоростей.
WX1:=wx0 * COS(alfa) - wz0 * SIN(alfa)
WY1:=WX1 * TAN(beta) + WY2 / COS(beta)
WZ1:=wx0 * SIN(alfa) + wz0 * COS(alfa)
WX11:=wx01 * COS(alfa) - wz01 * SIN(alfa)
WY11:=WX11 * TAN(beta) + WY21 / COS(beta)
WZ11:=wx01 * SIN(alfa) + wz01 * COS(alfa)
WX2:=WX1 * COS(beta) + WY1 * SIN(beta)
WX21:=WX11 * COS(beta) + WY11 * SIN(beta)
; Выражения для моментов количества движения.
QX1:=ix1 * WX1 - ixy1 * WY1 - ixz1 * WZ1
QY1:=iy1 * WY1 - IYX1 * WX1 - iyz1 * WZ1
QZ1:=iz1 * WZ1 - IZX1 * WX1 - IZY1 * WY1
QX2:=ix2 * WX2 - ixy2 * WY2 - ixz2 * WZ2
QY2:=iy2 * WY2 - IYX2 * WX2 - iyz2 * WZ2
QZ2:=iz2 * WZ2 - IZX2 * WX2 - IZY2 * WY2
QY11:=iy1 * WY11 - IYX1 * WX11 - iyz1 * WZ11
QX21:=ix2 * WX21 - ixy2 * WY21 - ixz2 * WZ21
QY21:=iy2 * WY21 - IYX2 * WX21 - iyz2 * WZ21
QZ21:=iz2 * WZ21 - IZX2 * WX21 - IZY2 * WY21
; Выражения для возмущающих моментов.
MY1:=QY11 - QZ1 * WX1 + QX1 * WZ1
MX2:=QX21 - QY2 * WZ2 + QZ2 * WY2
MY2:=QY21 - QZ2 * WX2 + QX2 * WZ2
MZ2:=QZ21 - QX2 * WY2 + QY2 * WX2
MY1IN:=MY1 + MX2 * SIN(beta) + MY2 * COS(beta)
; Блок решения.
; Упрощение выражения для Mz2.
MZ2:=ixy2 * wx0^2 * COS(beta)^2 * COS(alfa)^2 - ixy2 * wx0^2 * SIN(beta)^4 * COS(alfa)^2 / COS(beta)^2 - 2 * ixy2 * wx0^2 * COS(alfa)^2 - 2 * ixy2 * wx0 * wz0 * COS(beta)^2 * SIN(alfa) * COS(alfa) + 2 * ixy2 * wx0 * wz0 * SIN(beta)^4 * SIN(alfa) * COS(alfa) / COS(beta)^2 + 4 * ixy2 * wx0 * wz0 * SIN(alfa) * COS(alfa) - ixz2 * wx01 * COS(beta) * COS(alfa) - ixz2 * wx01 * SIN(beta)^2 * COS(alfa) / COS(beta) + ixy2 * wz0^2 * COS(beta)^2 * SIN(alfa)^2 - ixy2 * wz0^2 * SIN(beta)^4 * SIN(alfa)^2 / COS(beta)^2 - 2 * ixy2 * wz0^2 * SIN(alfa)^2 + ixz2 * wz01 * COS(beta) * SIN(alfa) + ixz2 * wz01 * SIN(beta)^2 * SIN(alfa) / COS(beta)
; Упрощение выражения для My1.
MY1IN:= - ixz2 * wx0^2 * COS(beta)^3 * COS(alfa)^2 + 2 * ixz2 * wx0^2 * COS(beta) * COS(alfa)^2 + ixz2 * wx0^2 * SIN(beta)^4 * COS(alfa)^2 / COS(beta) - ixy1 * wx0 * wz0 * TAN(beta) * COS(alfa)^2 + iyz1 * wx0^2 * TAN(beta) * COS(alfa)^2 + ix1 * wx0 * wz0 * COS(alfa)^2 + ixz1 * wx0^2 * COS(alfa)^2 - ixz1 * wz0^2 * COS(alfa)^2 - iz1 * wx0 * wz0 * COS(alfa)^2 + 2 * ixz2 * wx0 * wz0 * COS(beta)^3 * SIN(alfa) * COS(alfa) - 4 * ixz2 * wx0 * wz0 * COS(beta) * SIN(alfa) * COS(alfa) - 2 * ixz2 * wx0 * wz0 * SIN(beta)^4 * SIN(alfa) * COS(alfa) / COS(beta) - ixy1 * wx0^2 * TAN(beta) * SIN(alfa) * COS(alfa) + ixy1 * wz0^2 * TAN(beta) * SIN(alfa) * COS(alfa) - 2 * iyz1 * wx0 * wz0 * TAN(beta) * SIN(alfa) * COS(alfa) + ix1 * wx0^2 * SIN(alfa) * COS(alfa) - ix1 * wz0^2 * SIN(alfa) * COS(alfa) - 4 * ixz1 * wx0 * wz0 * SIN(alfa) * COS(alfa) - iz1 * wx0^2 * SIN(alfa) * COS(alfa) + iz1 * wz0^2 * SIN(alfa) * COS(alfa) + ix2 * wx01 * SIN(beta) * COS(beta) * COS(alfa) + ix2 * wx01 * SIN(beta)^3 * COS(alfa) / COS(beta) + iy1 * wx01 * TAN(beta) * COS(alfa) - ixy1 * wx01 * COS(alfa) - ixy2 * wx01 * COS(alfa) - iyz1 * wz01 * COS(alfa) - ixz2 * wz0^2 * COS(beta)^3 * SIN(alfa)^2 + 2 * ixz2 * wz0^2 * COS(beta) * SIN(alfa)^2 + ixz2 * wz0^2 * SIN(beta)^4 * SIN(alfa)^2 / COS(beta) + ixy1 * wx0 * wz0 * TAN(beta) * SIN(alfa)^2 + iyz1 * wz0^2 * TAN(beta) * SIN(alfa)^2 - ix1 * wx0 * wz0 * SIN(alfa)^2 - ixz1 * wx0^2 * SIN(alfa)^2 + ixz1 * wz0^2 * SIN(alfa)^2 + iz1 * wx0 * wz0 * SIN(alfa)^2 - ix2 * wz01 * SIN(beta) * COS(beta) * SIN(alfa) - ix2 * wz01 * SIN(beta)^3 * SIN(alfa) / COS(beta) - iy1 * wz01 * TAN(beta) * SIN(alfa) + ixy1 * wz01 * SIN(alfa) + ixy2 * wz01 * SIN(alfa) - iyz1 * wx01 * SIN(alfa)
Рабочая программа для пакета "DERIVE" с проведенными предварительными вычислениями.
; Входные данные.
; Переприсвоение моментов инерции.
IYX1:=ixy1
IYX2:=ixy2
IZX1:=ixz1
IZX2:=ixz2
IZY1:=iyz1
IZY2:=iyz2
; Выражения для угловых скоростей.
WX1:=wx0 * COS(alfa) - wz0 * SIN(alfa)
WY1:=WX1 * TAN(beta) + wy2 / COS(beta)
WZ1:=wx0 * SIN(alfa) + wz0 * COS(alfa)
WX11:=wx01 * COS(alfa) - wz01 * SIN(alfa)
WY11:=WX11 * TAN(beta) + wy21 / COS(beta)
WZ11:=wx01 * SIN(alfa) + wz01 * COS(alfa)
WX2:=WX1 * COS(beta) + WY1 * SIN(beta)
WX21:=WX11 * COS(beta) + WY11 * SIN(beta)
; Выражения для моментов количества движения.
QX1:=ix1 * WX1 - ixy1 * WY1 - ixz1 * WZ1
QY1:=iy1 * WY1 - IYX1 * WX1 - iyz1 * WZ1
QZ1:=iz1 * WZ1 - IZX1 * WX1 - IZY1 * WY1
QX2:=ix2 * WX2 - ixy2 * wy2 - ixz2 * wz2
QY2:=iy2 * wy2 - IYX2 * WX2 - iyz2 * wz2
QZ2:=iz2 * wz2 - IZX2 * WX2 - IZY2 * wy2
QY11:=iy1 * WY11 - IYX1 * WX11 - iyz1 * WZ11
QX21:=ix2 * WX21 - ixy2 * wy21 - ixz2 * wz21
QY21:=iy2 * wy21 - IYX2 * WX21 - iyz2 * wz21
QZ21:=iz2 * wz21 - IZX2 * WX21 - IZY2 * wy21
; Выражения для возмущающих моментов.
MY1:=QY11 - QZ1 * WX1 + QX1 * WZ1
MX2:=QX21 - QY2 * wz2 + QZ2 * wy2
MY2:=QY21 - QZ2 * WX2 + QX2 * wz2
MZ2:=QZ21 - QX2 * wy2 + QY2 * WX2
MY1IN:=MY1 + MX2 * SIN(beta) + MY2 * COS(beta)
; Блок решения.
; Раскрытие выражения для Mz2 по всем переменным.
MZ2:=ixy2 * wx0^2 * COS(beta)^2 * COS(alfa)^2 - ixy2 * wx0^2 * SIN(beta)^4 * COS(alfa)^2 / COS(beta)^2 - 2 * ixy2 * wx0^2 * COS(alfa)^2 - 2 * ixy2 * wx0 * wz0 * COS(beta)^2 * SIN(alfa) * COS(alfa) + 2 * ixy2 * wx0 * wz0 * SIN(beta)^4 * SIN(alfa) * COS(alfa) / COS(beta)^2 + 4 * ixy2 * wx0 * wz0 * SIN(alfa) * COS(alfa) - ix2 * wx0 * wy2 * COS(beta) * COS(alfa) - ixz2 * wx01 * COS(beta) * COS(alfa) + iy2 * wx0 * wy2 * COS(beta) * COS(alfa) - iyz2 * wx0 * wz2 * COS(beta) * COS(alfa) - ix2 * wx0 * wy2 * SIN(beta)^2 * COS(alfa) / COS(beta) - ixz2 * wx01 * SIN(beta)^2 * COS(alfa) / COS(beta) + iy2 * wx0 * wy2 * SIN(beta)^2 * COS(alfa) / COS(beta) - iyz2 * wx0 * wz2 * SIN(beta)^2 * COS(alfa) / COS(beta) - 2 * ixy2 * wx0 * wy2 * SIN(beta)^3 * COS(alfa) / COS(beta)^2 - 2 * ixy2 * wx0 * wy2 * SIN(beta) * COS(alfa) + ixy2 * wz0^2 * COS(beta)^2 * SIN(alfa)^2 - ixy2 * wz0^2 * SIN(beta)^4 * SIN(alfa)^2 / COS(beta)^2 - 2 * ixy2 * wz0^2 * SIN(alfa)^2 + ix2 * wy2 * wz0 * COS(beta) * SIN(alfa) + ixz2 * wz01 * COS(beta) * SIN(alfa) - iy2 * wy2 * wz0 * COS(beta) * SIN(alfa) + iyz2 * wz0 * wz2 * COS(beta) * SIN(alfa) + ix2 * wy2 * wz0 * SIN(beta)^2 * SIN(alfa) / COS(beta) + ixz2 * wz01 * SIN(beta)^2 * SIN(alfa) / COS(beta) - iy2 * wy2 * wz0 * SIN(beta)^2 * SIN(alfa) / COS(beta) + iyz2 * wz0 * wz2 * SIN(beta)^2 * SIN(alfa) / COS(beta) + 2 * ixy2 * wy2 * wz0 * SIN(beta)^3 * SIN(alfa) / COS(beta)^2 + 2 * ixy2 * wy2 * wz0 * SIN(beta) * SIN(alfa) - ix2 * wy2^2 * TAN(beta) - ixz2 * wy21 * TAN(beta) + iy2 * wy2^2 * TAN(beta) - iyz2 * wy2 * wz2 * TAN(beta) - ixy2 * wy2^2 * TAN(beta)^2 + ixy2 * wy2^2 + ixz2 * wy2 * wz2 - iyz2 * wy21 + iz2 * wz21
; Раскрытие скобок по всем переменным в выражении
; для My1.
MY1IN:= - ixz2 * wx0^2 * COS(beta)^3 * COS(alfa)^2 + 2 * ixz2 * wx0^2 * COS(beta) * COS(alfa)^2 + ixz2 * wx0^2 * SIN(beta)^4 * COS(alfa)^2 / COS(beta) - ixy1 * wx0 * wz0 * TAN(beta) * COS(alfa)^2 + iyz1 * wx0^2 * TAN(beta) * COS(alfa)^2 + ix1 * wx0 * wz0 * COS(alfa)^2 + ixz1 * wx0^2 * COS(alfa)^2 - ixz1 * wz0^2 * COS(alfa)^2 - iz1 * wx0 * wz0 * COS(alfa)^2 + 2 * ixz2 * wx0 * wz0 * COS(beta)^3 * SIN(alfa) * COS(alfa) - 4 * ixz2 * wx0 * wz0 * COS(beta) * SIN(alfa) * COS(alfa) - 2 * ixz2 * wx0 * wz0 * SIN(beta)^4 * SIN(alfa) * COS(alfa) / COS(beta) - ixy1 * wx0^2 * TAN(beta) * SIN(alfa) * COS(alfa) + ixy1 * wz0^2 * TAN(beta) * SIN(alfa) * COS(alfa) - 2 * iyz1 * wx0 * wz0 * TAN(beta) * SIN(alfa) * COS(alfa) + ix1 * wx0^2 * SIN(alfa) * COS(alfa) - ix1 * wz0^2 * SIN(alfa) * COS(alfa) - 4 * ixz1 * wx0 * wz0 * SIN(alfa) * COS(alfa) - iz1 * wx0^2 * SIN(alfa) * COS(alfa) + iz1 * wz0^2 * SIN(alfa) * COS(alfa) + ix2 * wx01 * SIN(beta) * COS(beta) * COS(alfa) + ixy2 * wx0 * wz2 * SIN(beta) * COS(beta) * COS(alfa) + ixz2 * wx0 * wy2 * SIN(beta) * COS(beta) * COS(alfa) + ix2 * wx01 * SIN(beta)^3 * COS(alfa) / COS(beta) + ixy2 * wx0 * wz2 * SIN(beta)^3 * COS(alfa) / COS(beta) + ixz2 * wx0 * wy2 * SIN(beta)^3 * COS(alfa) / COS(beta) + iy1 * wx01 * TAN(beta) * COS(alfa) - ixy1 * wy2 * wz0 * COS(alfa) / COS(beta) + iyz1 * wx0 * wy2 * COS(alfa) / COS(beta) + ix2 * wx0 * wz2 * COS(alfa) - ixy1 * wx01 * COS(alfa) - ixy2 * wx01 * COS(alfa) - iyz1 * wz01 * COS(alfa) + iyz2 * wx0 * wy2 * COS(alfa) - iz2 * wx0 * wz2 * COS(alfa) - ixz2 * wz0^2 * COS(beta)^3 * SIN(alfa)^2 + 2 * ixz2 * wz0^2 * COS(beta) * SIN(alfa)^2 + ixz2 * wz0^2 * SIN(beta)^4 * SIN(alfa)^2 / COS(beta) + ixy1 * wx0 * wz0 * TAN(beta) * SIN(alfa)^2 + iyz1 * wz0^2 * TAN(beta) * SIN(alfa)^2 - ix1 * wx0 * wz0 * SIN(alfa)^2 - ixz1 * wx0^2 * SIN(alfa)^2 + ixz1 * wz0^2 * SIN(alfa)^2 + iz1 * wx0 * wz0 * SIN(alfa)^2 - ix2 * wz01 * SIN(beta) * COS(beta) * SIN(alfa) - ixy2 * wz0 * wz2 * SIN(beta) * COS(beta) * SIN(alfa) - ixz2 * wy2 * wz0 * SIN(beta) * COS(beta) * SIN(alfa) - ix2 * wz01 * SIN(beta)^3 * SIN(alfa) / COS(beta) - ixy2 * wz0 * wz2 * SIN(beta)^3 * SIN(alfa) / COS(beta) - ixz2 * wy2 * wz0 * SIN(beta)^3 * SIN(alfa) / COS(beta) - iy1 * wz01 * TAN(beta) * SIN(alfa) - ixy1 * wx0 * wy2 * SIN(alfa) / COS(beta) - iyz1 * wy2 * wz0 * SIN(alfa) / COS(beta) - ix2 * wz0 * wz2 * SIN(alfa) + ixy1 * wz01 * SIN(alfa) + ixy2 * wz01 * SIN(alfa) - iyz1 * wx01 * SIN(alfa) - iyz2 * wy2 * wz0 * SIN(alfa) + iz2 * wz0 * wz2 * SIN(alfa) - ixy2 * wy2 * wz2 * COS(beta) - ixz2 * wz2^2 * COS(beta) + iy2 * wy21 * COS(beta) - iyz2 * wz21 * COS(beta) + ix2 * wy21 * SIN(beta)^2 / COS(beta) + ixy2 * wy2 * wz2 * SIN(beta)^2 / COS(beta) + iy1 * wy21 / COS(beta) + ix2 * wy2 * wz2 * SIN(beta) - 2 * ixy2 * wy21 * SIN(beta) - ixz2 * wz21 * SIN(beta) - iy2 * wy2 * wz2 * SIN(beta) + iyz2 * wz2^2 * SIN(beta)
Рабочая программа для пакета “DERIVE” определения коэффициентов при степенях s в полиноме знаменателя передаточной функции разомкнутой системы Wp(s).
; Входные данные.
; Определитель исходной матрицы.
DET([[m1 * s^2 + d01 * s + d12 * s + c01 + c12,- d12 * s - c12,0,0,0],
[ - d12 * s - c12, m2 * s^2 + d12 * s + d23 * s + c12, - d23 * s, 0, 0],
[0, - d23 * s, m3 * s^2 + (d23 + d34) * s + c34, - (d34 * s + c34), 0],
[0, 0, - (d34 * s + c34), m4 * s^2 + (d34 + d45) * s + (c34 + c45), - (d45 * s + c45)],
[0, 0, 0, - (d45 * s + c45), m5 * s^2 + d45 * s + c45]])
; Блок решения.
; Результат нахождения определителя.
m1 * m2 * m3 * m4 * m5 * s^10 + s^9 * (d01 * m2 * m3 * m4 * m5 + d12 * (m1 * m3 * m4 * m5 + m2 * m3 * m4 * m5) + m1 * (d23 * m4 * m5 * (m2 + m3) + m2 * (d34 * m5 * (m3 + m4) + d45 * m3 * (m4 + m5)))) + s^8 * (c01 * m2 * m3 * m4 * m5 + c12 * (m1 * m3 * m4 * m5 + m2 * m3 * m4 * m5) + c34 * m1 * m2 * m5 * (m3 + m4) + c45 * m1 * m2 * m3 * (m4 + m5) + d01 * (d12 * m3 * m4 * m5 + d23 * m4 * m5 * (m2 + m3) + m2 * (d34 * m5 * (m3 + m4) + d45 * m3 * (m4 + m5))) + d12 * (d23 * (m1 * m4 * m5 + m4 * m5 * (m2 + m3)) + (m1 + m2) * (d34 * m5 * (m3 + m4) + d45 * m3 * (m4 + m5))) + m1 * (d23 * (d34 * m5 * (m2 + m3 + m4) + d45 * (m4 + m5) * (m2 + m3)) + d34 * d45 * m2 * (m3 + m4 + m5))) + s^7 * (c01 * (d12 * m3 * m4 * m5 + d23 * m4 * m5 * (m2 + m3) + m2 * (d34 * m5 * (m3 + m4) + d45 * m3 * (m4 + m5))) + c12 * (d01 * m3 * m4 * m5 + d23 * (m1 * m4 * m5 + m4 * m5 * (m2 + m3)) + (m1 + m2) * (d34 * m5 * (m3 + m4) + d45 * m3 * (m4 + m5))) + c34 * (d01 * m2 * m5 * (m3 + m4) + d12 * (m1 * m5 * (m3 + m4) + m2 * m5 * (m3 + m4)) + m1 * (d23 * m5 * (m2 + m3 + m4) + d45 * m2 * (m3 + m4 + m5))) + c45 * (d01 * m2 * m3 * (m4 + m5) + d12 * (m1 * m3 * (m4 + m5) + m2 * m3 * (m4 + m5)) + m1 * (d23 * (m4 + m5) * (m2 + m3) + d34 * m2 * (m3 + m4 + m5))) + d01 * (d12 * (d23 * m4 * m5 + d34 * m5 * (m3 + m4) + d45 * m3 * (m4 + m5)) + d23 * (d34 * m5 * (m2 + m3 + m4) + d45 * (m4 + m5) * (m2 + m3)) + d34 * d45 * m2 * (m3 + m4 + m5)) + d12 * (d23 * (d34 * (m1 * m5 + m5 * (m2 + m3 + m4)) + d45 * (m1 * (m4 + m5) + (m4 + m5) * (m2 + m3))) + d34 * d45 * (m1 * (m3 + m4 + m5) + m2 * (m3 + m4 + m5))) + d23 * d34 * d45 * m1 * (m2 + m3 + m4 + m5)) + s^6 * (c01 * (c12 * m3 * m4 * m5 + c34 * m2 * m5 * (m3 + m4) + c45 * m2 * m3 * (m4 + m5) + d12 * (d23 * m4 * m5 + d34 * m5 * (m3 + m4) + d45 * m3 * (m4 + m5)) + d23 * (d34 * m5 * (m2 + m3 + m4) + d45 * (m4 + m5) * (m2 + m3)) + d34 * d45 * m2 * (m3 + m4 + m5)) + c12 * (c34 * (m1 * m5 * (m3 + m4) + m2 * m5 * (m3 + m4)) + c45 * (m1 * m3 * (m4 + m5) + m2 * m3 * (m4 + m5)) + d01 * (d23 * m4 * m5 + d34 * m5 * (m3 + m4) + d45 * m3 * (m4 + m5)) + d23 * (d34 * (m1 * m5 + m5 * (m2 + m3 + m4)) + d45 * (m1 * (m4 + m5) + (m4 + m5) * (m2 + m3))) + d34 * d45 * (m1 * (m3 + m4 + m5) + m2 * (m3 + m4 + m5))) + c34 * (c45 * m1 * m2 * (m3 + m4 + m5) + d01 * (d12 * m5 * (m3 + m4) + d23 * m5 * (m2 + m3 + m4) + d45 * m2 * (m3 + m4 + m5)) + d12 * (d23 * (m1 * m5 + m5 * (m2 + m3 + m4)) + d45 * (m1 * (m3 + m4 + m5) + m2 * (m3 + m4 + m5))) + d23 * d45 * m1 * (m2 + m3 + m4 + m5)) + c45 * (d01 * (d12 * m3 * (m4 + m5) + d23 * (m4 + m5) * (m2 + m3) + d34 * m2 * (m3 + m4 + m5)) + d12 * (d23 * (m1 * (m4 + m5) + (m4 + m5) * (m2 + m3)) + d34 * (m1 * (m3 + m4 + m5) + m2 * (m3 + m4 + m5))) + d23 * d34 * m1 * (m2 + m3 + m4 + m5)) + d01 * (d12 * (d23 * (d34 * m5 + d45 * (m4 + m5)) + d34 * d45 * (m3 + m4 + m5)) + d23 * d34 * d45 * (m2 + m3 + m4 + m5)) + d12 * d23 * d34 * d45 * (m1 + m2 + m3 + m4 + m5)) + s^5 * (c01 * (c12 * (d23 * m4 * m5 + d34 * m5 * (m3 + m4) + d45 * m3 * (m4 + m5)) + c34 * (d12 * m5 * (m3 + m4) + d23 * m5 * (m2 + m3 + m4) + d45 * m2 * (m3 + m4 + m5)) + c45 * (d12 * m3 * (m4 + m5) + d23 * (m4 + m5) * (m2 + m3) + d34 * m2 * (m3 + m4 + m5)) + d12 * (d23 * (d34 * m5 + d45 * (m4 + m5)) + d34 * d45 * (m3 + m4 + m5)) + d23 * d34 * d45 * (m2 + m3 + m4 + m5)) + c12 * (c34 * (d01 * m5 * (m3 + m4) + d23 * (m1 * m5 + m5 * (m2 + m3 + m4)) + d45 * (m1 * (m3 + m4 + m5) + m2 * (m3 + m4 + m5))) + c45 * (d01 * m3 * (m4 + m5) + d23 * (m1 * (m4 + m5) + (m4 + m5) * (m2 + m3)) + d34 * (m1 * (m3 + m4 + m5) + m2 * (m3 + m4 + m5))) + d01 * (d23 * (d34 * m5 + d45 * (m4 + m5)) + d34 * d45 * (m3 + m4 + m5)) + d23 * d34 * d45 * (m1 + m2 + m3 + m4 + m5)) + c34 * (c45 * (d01 * m2 * (m3 + m4 + m5) + d12 * (m1 * (m3 + m4 + m5) + m2 * (m3 + m4 + m5)) + d23 * m1 * (m2 + m3 + m4 + m5)) + d01 * (d12 * (d23 * m5 + d45 * (m3 + m4 + m5)) + d23 * d45 * (m2 + m3 + m4 + m5)) + d12 * d23 * d45 * (m1 + m2 + m3 + m4 + m5)) + c45 * (d01 * (d12 * (d23 * (m4 + m5) + d34 * (m3 + m4 + m5)) + d23 * d34 * (m2 + m3 + m4 + m5)) + d12 * d23 * d34 * (m1 + m2 + m3 + m4 + m5)) + d01 * d12 * d23 * d34 * d45) + s^4 * (c01 * (c12 * (c34 * m5 * (m3 + m4) + c45 * m3 * (m4 + m5) + d23 * (d34 * m5 + d45 * (m4 + m5)) + d34 * d45 * (m3 + m4 + m5)) + c34 * (c45 * m2 * (m3 + m4 + m5) + d12 * (d23 * m5 + d45 * (m3 + m4 + m5)) + d23 * d45 * (m2 + m3 + m4 + m5)) + c45 * (d12 * (d23 * (m4 + m5) + d34 * (m3 + m4 + m5)) + d23 * d34 * (m2 + m3 + m4 + m5)) + d12 * d23 * d34 * d45) + c12 * (c34 * (c45 * (m1 * (m3 + m4 + m5) + m2 * (m3 + m4 + m5)) + d01 * (d23 * m5 + d45 * (m3 + m4 + m5)) + d23 * d45 * (m1 + m2 + m3 + m4 + m5)) + c45 * (d01 * (d23 * (m4 + m5) + d34 * (m3 + m4 + m5)) + d23 * d34 * (m1 + m2 + m3 + m4 + m5)) + d01 * d23 * d34 * d45) + c34 * (c45 * (d01 * (d12 * (m3 + m4 + m5) + d23 * (m2 + m3 + m4 + m5)) + d12 * d23 * (m1 + m2 + m3 + m4 + m5)) + d01 * d12 * d23 * d45) + c45 * d01 * d12 * d23 * d34) + s^3 * (c01 * (c12 * (c34 * (d23 * m5 + d45 * (m3 + m4 + m5)) + c45 * (d23 * (m4 + m5) + d34 * (m3 + m4 + m5)) + d23 * d34 * d45) + c34 * (c45 * (d12 * (m3 + m4 + m5) + d23 * (m2 + m3 + m4 + m5)) + d12 * d23 * d45) + c45 * d12 * d23 * d34) + c12 * (c34 * (c45 * (d01 * (m3 + m4 + m5) + d23 * (m1 + m2 + m3 + m4 + m5)) + d01 * d23 * d45) + c45 * d01 * d23 * d34) + c34 * c45 * d01 * d12 * d23) + s^2 * (c01 * (c12 * (c34 * (c45 * (m3 + m4 + m5) + d23 * d45) + c45 * d23 * d34) + c34 * c45 * d12 * d23) + c12 * c34 * c45 * d01 * d23) + c01 * c12 * c34 * c45 * d23 * s
Рабочая программа для пакета “DERIVE” определения коэффициентов при степенях s в полиноме числителя передаточной функции разомкнутой системы Wp(s).; Входные данные.
; Определитель от исходной матрицы.
DET([[m1 * s^2 + d01 * s + d12 * s + c01 + c12, - d12 * s - c12,0,0,0],
[- d12 * s - c12, m2 * s^2 + d12 * s + d23 * s + c12,- d23 * s, k * x4,0],
[0, - d23 * s, m3 * s^2 + (d23 + d34) * s + c34, - k * x4, 0],
[0, 0, - (d34 * s + c34), 0, - (d45 * s + c45)],
[0, 0, 0, 0, m5 * s^2 + d45 * s + c45]])
; Блок решения.
; Результат нахождения определителя.
- d34 * k * m1 * m2 * m5 * x4 * s^7 - k * x4 * s^6 * (c34 * m1 * m2 * m5 + d34 * (d01 * m2 * m5 + d12 * m5 * (m1 + m2) + d45 * m1 * m2)) - k * x4 * s^5 * (c01 * d34 * m2 * m5 + c12 * d34 * m5 * (m1 + m2) + c34 * (d01 * m2 * m5 + d12 * m5 * (m1 + m2) + d45 * m1 * m2) + d34 * (c45 * m1 * m2 + d01 * (d12 * m5 + d45 * m2) + d12 * d45 * (m1 + m2))) - k * x4 * s^4 * (c01 * (c34 * m2 * m5 + d34 * (d12 * m5 + d45 * m2)) + c12 * (c34 * m5 * (m1 + m2) + d34 * (d01 * m5 + d45 * (m1 + m2))) + c34 * (c45 * m1 * m2 + d01 * (d12 * m5 + d45 * m2) + d12 * d45 * (m1 + m2)) + d34 * (c45 * (d01 * m2 + d12 * (m1 + m2)) + d01 * d12 * d45)) - k * x4 * s^3 * (c01 * (c12 * d34 * m5 + c34 * (d12 * m5 + d45 * m2) + d34 * (c45 * m2 + d12 * d45)) + c12 * (c34 * (d01 * m5 + d45 * (m1 + m2)) + d34 * (c45 * (m1 + m2) + d01 * d45)) + c34 * (c45 * (d01 * m2 + d12 * (m1 + m2)) + d01 * d12 * d45) + c45 * d01 * d12 * d34) - k * x4 * s^2 * (c01 * (c12 * (c34 * m5 + d34 * d45) + c34 * (c45 * m2 + d12 * d45) + c45 * d12 * d34) + c12 * (c34 * (c45 * (m1 + m2) + d01 * d45) + c45 * d01 * d34) + c34 * c45 * d01 * d12) - k * x4 * s * (c01 * (c12 * (c34 * d45 + c45 * d34) + c34 * c45 * d12) + c12 * c34 * c45 * d01) - c01 * c12 * c34 * c45 * k * x4
Описание электронной части канала стабилизации.
Описание структурной схемы канала стабилизации.
Структурная схема канала представлена на рис.1. Взаимодействие между элементами структурной схемы следующее.
Чувствительным элементом, измеряющим отклонение стабилизированной платформы от заданного положения является датчик угловой скорости (ДУС), роль которого выполняет волоконно-оптический гироскоп (ВОГ), сигнал на выходе которого пропорционален угловой скорости вращения платформы. Поэтому для устранения статической ошибки стабилизации сигнал с выхода ВОГ поступает на интегратор, на выходе которого формируется напряжение пропорциональное уже не скорости, а углу отклонения платформы.
Далее это напряжение поступает на вход корректирующего звена, которое формирует необходимый вид ЛАХ для обеспечения устойчивости работы ГС. После предварительного усиления напряжение пропорциональ-ное углу отклонения платформы поступает на схему гальванической развязки, которая обеспечивает развязку по цепям питания между схемой управления и усилителем мощности (УМ), между сильноточными и слаботочными цепями схемы. Это необходимо для увеличения помехозащищенности канала обратной связи, кроме того это позволяет запитывать УМ непосредственно от первичного источника питания (аккумулятора или внешнего блока питания) без использования мощных преобразователей напряжения для питания УМ.
Далее сигнал подается на вход усилителя мощности, который обеспечивает подачу управляющего напряжения на двигатели стабилизации. УМ выполнен импульсным с использованием широтно-импульсной модуляции управляющего напряжения. Это позволяет повысить КПД УМ, что является актуальным с учетом требований к необходимости получения больших скоростей и ускорений управления положением телекамеры, что требует применения мощных двигателей стабилизации.
Одной из особенностей использования ВОГ является его высокая чувствительность к воздействию внешних электрических возмущений, что приводит к нарушению работы ВОГ вплоть до выхода его из строя. Поэтому в состав канала стабилизации необходимо обязательное включение специальной схемы защиты ВОГ.
Описание и расчет элементов электрической схемы канала обратной связи ГС ТК.Описание схемы защиты и подачи питания на ВОГ.
Особенностью эксплуатации ВОГ, в отличие от механических гироскопов, является его высокая чувствительность к превышениям допустимых электрических воздействий по цепям питания и выходным цепям. Кроме того требуется определенная последовательность включения во времени различных цепей. Поэтому для подачи питания на ВОГ была разработана схема питания и защиты ВОГ, которая представлена на рис.2.
Данная схема обеспечивает:
— задержку подачи напряжения ± 15 В относительно напряжения питания суперлюминесцентного диода (СЛД) на время 0.5 с.;
— защиту СЛД и ВОГа от перепутки полярности при подаче напряжения питания;
— отключение напряжения ± 15 В.
а) при обрыве любого из питающих проводников или “общего” провода;
б) при исчезновении напряжения на СЛД;
— обеспечивает фильтрацию напряжения по цепям питания СЛД и ±15 В.
Описание работы схемы.
Через выключатель В1, диод VD1, резистор R1 осуществляется подача тока в СЛД ВОГа. Конденсаторы C1, C2 фильтрующие, их номинал 10.0 мкФ. и 0.22 мкФ. выбран в соответствии с рекомендациями приведенными в инструкции по эксплуатации ВОГ. Резистор R1 задает ток СЛД, его номинал определяется по формуле:
(Uвх.-3) (15 - 3)
![]()
![]() R1
= = = 130 Ом.
R1
= = = 130 Ом.
Iслд. 0.09
где Iслд. - номинальный ток через СЛД.
Диоды VD1, VD7, VD8 защищают ВОГ при подаче напряжения обратной полярности. В качестве этих диодов могут быть применены любые диоды с допустимым прямым током не менее 0.3 А, в макете использованы диоды типа КД212. Диод VD3 типа КД522 предохраняет СЛД от наведенных случайных импульсов обратной полярности.
На элементах R2, R3, C3, VD2, VD4, VT1 выполнена схема задержки подачи на ВОГ напряжения ±15 В и его снятия при исчезновении напряжения на СЛД. Работает схема следующим образом. При появлении напряжения питания на аноде СЛД конденсатор C3 начинает заряжаться через резистор R3. Когда напряжение на нем достигнет уровня около 1.2 В открывается транзистор VT1 и через ограничительный резистор R4 в базу транзистора VT2 поступает открывающий его ток, при этом срабатывает реле Р1 и через контакты Р1.1 и Р1.2 напряжение ±15В поступает на ВОГ. Если напряжение на СЛД по какой-либо причине исчезнет, то конденсатор C3 быстро разряжается через диод VD2 и резистор R2, транзисторы VT1 и VT2 закрываются и реле размыкает цепь подачи ±15 В на ВОГ.
Диод VD4 поднимает порог открывания транзистора VT1 на 0.5 В. Диод VD5 защищает транзистор VT2 от пробоя при отключении реле. Диоды VD3, VD4, VD5 типа КД522.
При выборе величины R3 = 100 кОм и C3 = 10.0 мкФ. постоянная времени цепи задержки Т будет равна:
Т = 2·3.14·R3·C3 = 6.28 · 100·103 ·10.0·10-6 = 6.28 c.
Реально открывание транзистора VT1 происходит примерно через 0.5 с.
Величина резистора R4 при заданном токе базы транзистора VT2 Iб2 = 2 мА. определяется по следующей формуле:
15 B. 15
![]()
![]() R4
= = = 7500 Ом. ( Выбираю
R4 = 10 кОм )
R4
= = = 7500 Ом. ( Выбираю
R4 = 10 кОм )
Iб2. 0.002
Резисторы R5, R6 и конденсаторы C4...C7 образуют фильтр по цепи питания ±15 В. Их величины не рассчитывались, а выбраны в соответствие с рекомендациями приведенными в инструкции по эксплуатации ВОГ.
R5 = R6 = 1 Ом, C4 = C6 = 0.22 мкФ, C5 = C7 = 10.0 мкФ.
Транзистор VT1 типа КТ315, VT2 типа КТ502. Реле типа РЭС60, РЭС80. Стабилитрон VD6 необходим при использовании реле с напряжением удержания менее 15 В. Он служит для обеспечения надежного выключения реле при пропадании одного из напряжений ±15 В. В макете использован стабилитрон типа Д814А имеющий напряжение стабилизации 8 В.
Описание элементов электрической схемы канала стабилизации.
Электрическая схема слаботочной части канала стабилизации представлена на рис.3. Рассмотрим элементы схемы.
1. Интегратор и предварительный усилитель.
Особенностью использования ДУСа в качестве чувствительного элемента (ЧЭ) ИГС является необходимость применения интегрирующих звеньев в канале стабилизации для получения необходимого коэффициента усиления в низкочастотной области ЛАХ. При использовании идеального интегратора происходит стабилизация по углу вместо стабилизации по скорости.
Интегратор выполнен на микросхеме DA1. Его передаточная функция при R1 = R5 = R имеет следующий вид [1]:
- Ku'
![]() Wи(s) =
Wи(s) =
(s/[Ku'·fср] + 1) · (s·Ku'·R· C + 1)
где Кu' - коэффициент усиления ОУ без цепей обратной связи;
fср - частота единичного усиления ОУ;
С = C1.
В качестве DA1 применен ОУ типа КР140УД18 имеющий следующие характеристики [2]:
Uпит.ном.[B] 2х15 (6..18);
Ku' 50000;
Uсм.[mB] 10;
Iвх[нА] 1;
DIвх[нА] 0.1;
fср[Гц] 1;
Vu [B/мкс] 5;
Rвх[МОм] 1000000.
Выбор данного типа ОУ обусловлен его высоким входным сопротивлением Rвх. и повышенной частотой единичного усиления fср. При подстановке этих параметров в выражение для Wи(s) получается выражение следующего вида (при R=R1=1 МОм, С=C1= 2.2 мкФ):
-5·104 -5·104
![]()
![]() Wи(s)
= =
Wи(s)
= =
(s/5·1010+1)·(s·1.1·104+1) (T1·s+1) · (T2·s+1)
В данном выражении T1
Похожие работы
... за счет использования двигателя стабилизации меньших габаритов, имеющего меньший момент сухого трения вокруг оси вращения и меньший коэффициент демпфирования. Габаритные размеры гиростабилизатора телекамеры с наружным кардановым подвесом оказываются меньше, чем с внутренним, т.к. в последнем случае для получения достаточных рабочих углов поворота платформы необходимо выполнение подвеса по ...
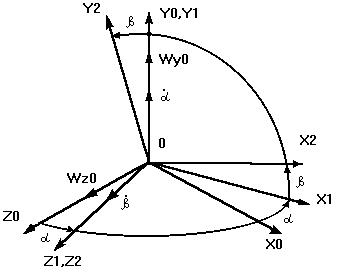
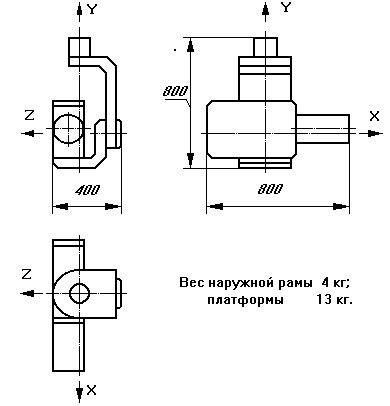
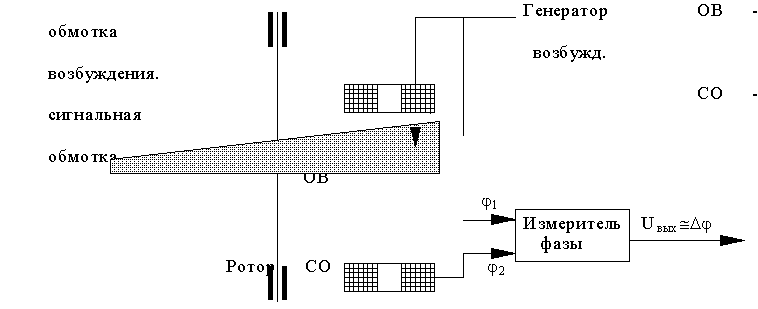
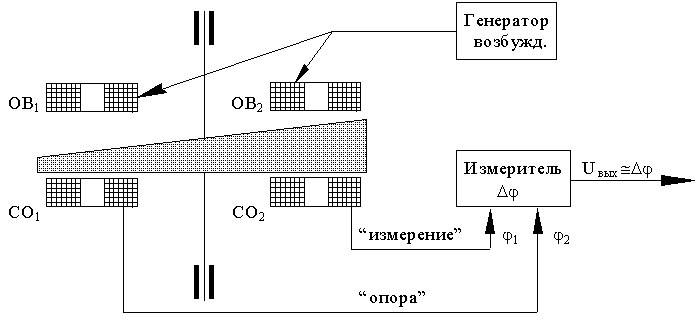
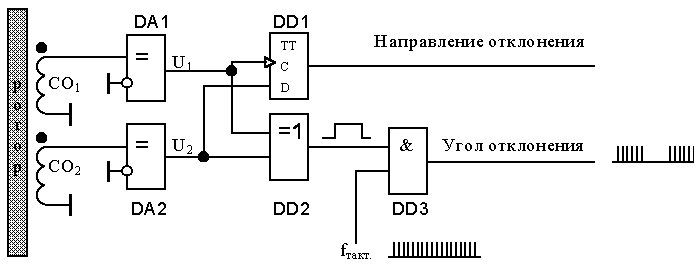
0 комментариев