Лабораторные работы по физике

Нижегородский Государственный Технический Университет.

Лабораторная работа по физике №2-23.

Изучение основных правил работы с

радиоизмерительными приборами.

Выполнил студент

Группы 99 – ЭТУ

Наумов Антон Николаевич

Проверил:

Н. Новгород 2000г.

Цель работы: знакомство с основными характеристиками радиоизмерительных приборов, правилами их подключения к измеряемому объекту, методикой проведения измерений и оценкой их погрешностей.

Задание №1: Измерение напряжения сигнала генератора.

Приборы: генератор сигнала Г3, вольтметры В3 и В7.

Экспериментальная часть.

1). Установили на генераторе частоту выходного сигнала f = 5кГц, напряжение U = 2В.

Измерили вольтметром В3 выходное напряжение U_x=2В.

Погрешность измерения.

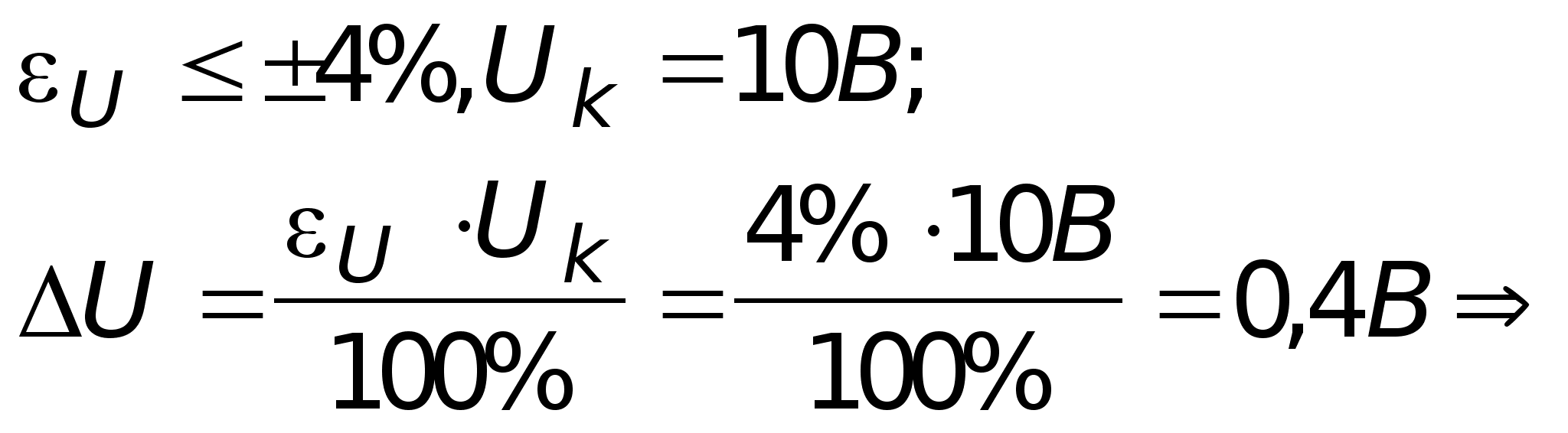U=U_x  U=(2  0,4) B.

2). Измерили вольтметром В7 выходное напряжение U_x=2,01В.

Погрешность измерения.

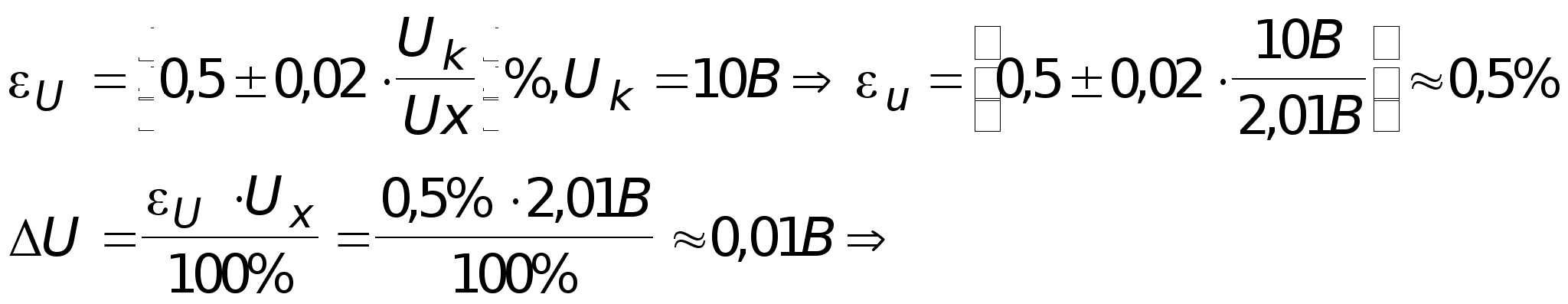
U=U_x  U=(2,01  0,01) B.

Задание №2: Анализ формы и измерение параметров синусоидального сигнала с помощью осциллографа.

Приборы: генератор сигнала Г3, вольтметры В3 и В7, осциллограф С1.

Экспериментальная часть.

1). Установили на генераторе Г3 напряжение U = 2В.

Измерили вольтметром В3 выходное напряжение U_x=2В; на вольтметре В7: U_x=2В.

Получили на экране осциллографа изображение:

АО=1,4 см, Х = 4 см.

Измерим амплитуду сигнала:

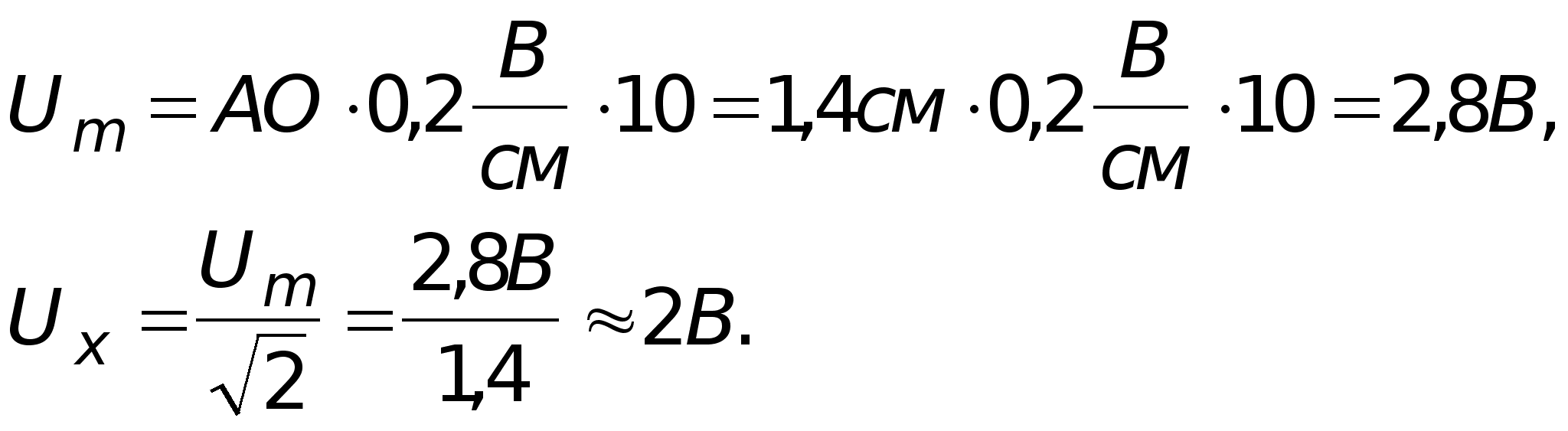
Показания осциллографа совпадают с показаниями вольтметров.

2). Измерили период (Т) и частоту сигнала (f):

Показания осциллографа совпадают со значением на шкале генератора.

Задание №3: Измерение частоты с помощью частотомера и осциллографа.

Приборы: генератор сигнала Г3, вольтметры В3 и В7, осциллограф С1, частотомер Ф.

Экспериментальная часть.

1). Измерили частоту сигнала частотомером:

Погрешность измерения:

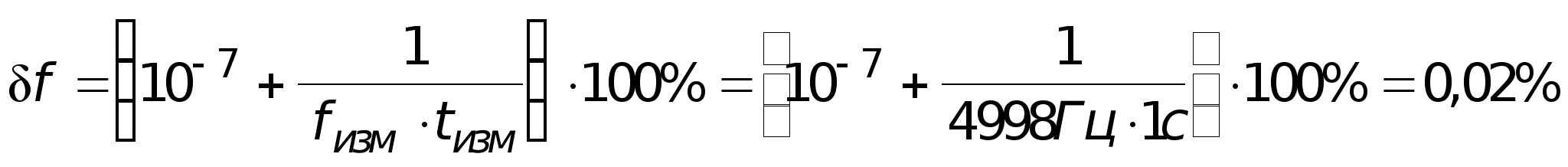
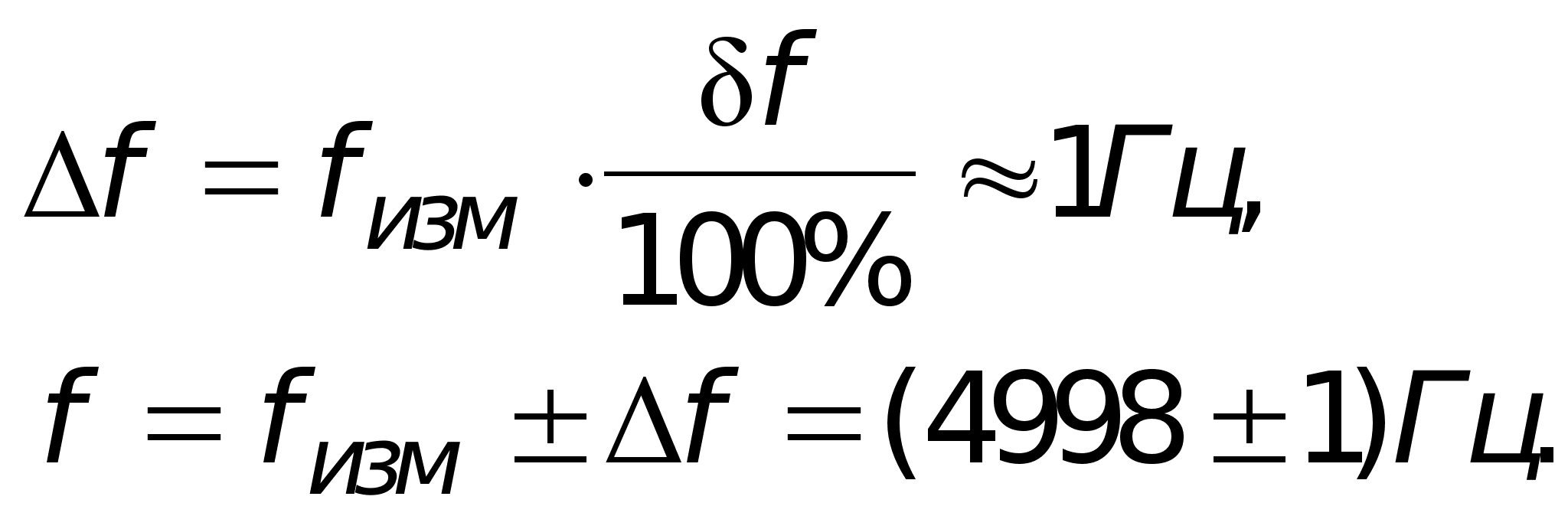
Показания генератора: f_x = 5кГц.

2). Рассчитаем частоту сигнала по показаниям осциллографа:

Х = 2 см.

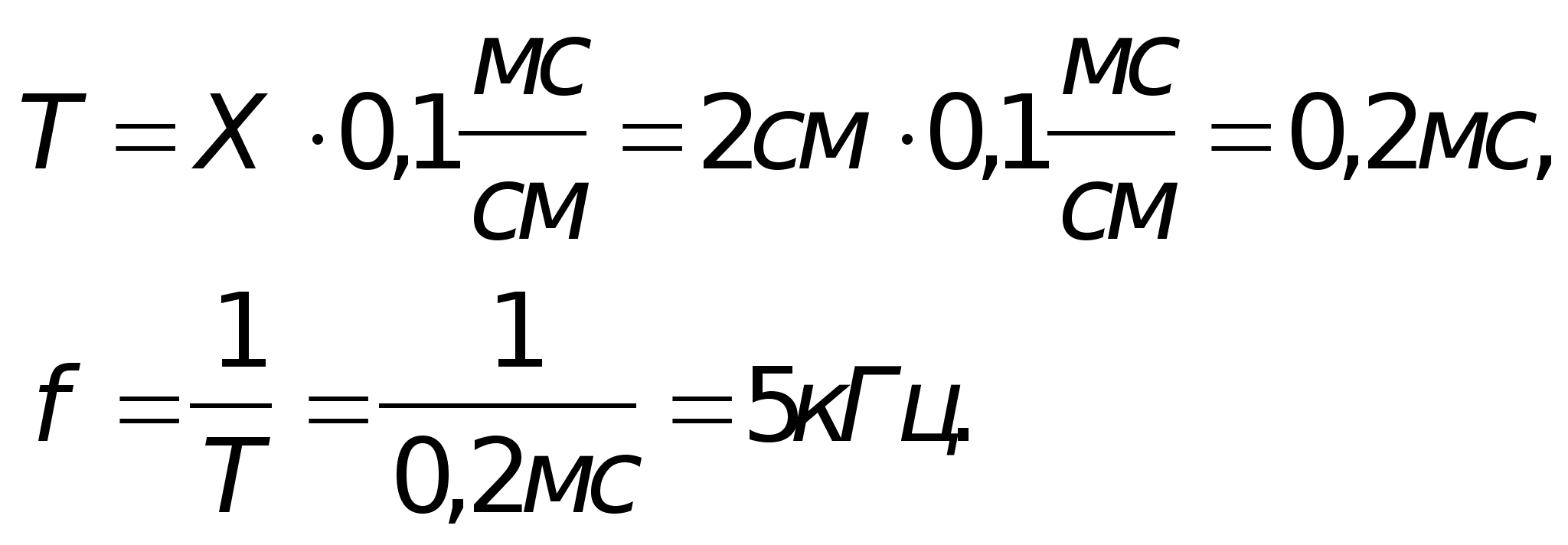
Показания всех приборов совпадают.

Задание №4: Измерение фаз двух синусоидальных сигналов с помощью осциллографа.

Приборы: генератор сигнала Г3, осциллограф С1, схема RC.

Экспериментальная часть.

OA = 1,9 см, ОВ = 1,7 см.

Т.к. , а  - разность фаз синусоидальных

сигналов, то

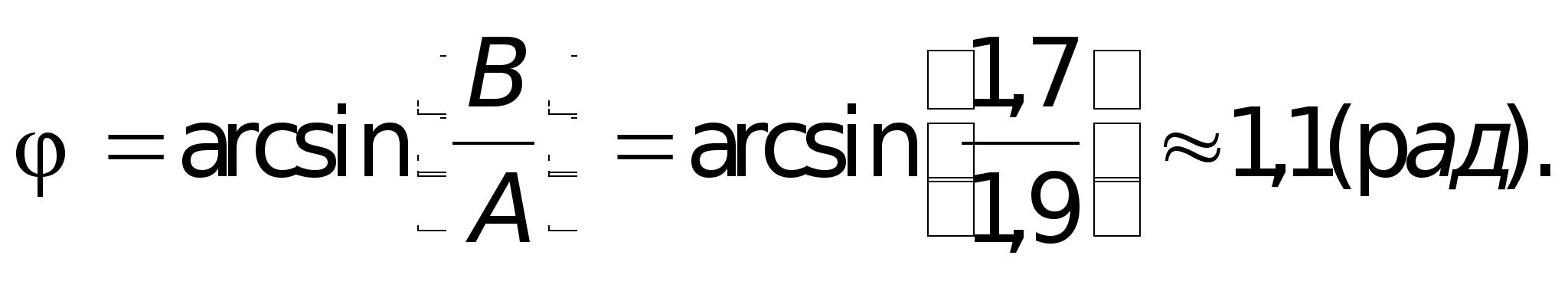
Задание №5: Анализ формы и измерение параметров импульсного сигнала с помощью осциллографа.

Приборы: генератор сигнала Г5, осциллограф С1.

Экспериментальная часть.

1).Установим длительность импульсов  = 500 мкс, частоту повторений f_П=490Гц, амплитуду U_m=1,32B

2).Получили на экране следующее изображение:

Вычислим амплитуду импульсов:

Полученный результат совпадает с показаниями вольтметра генератора.

Измерим длительность импульсов:

Измерим период и частоту повторений импульсов:

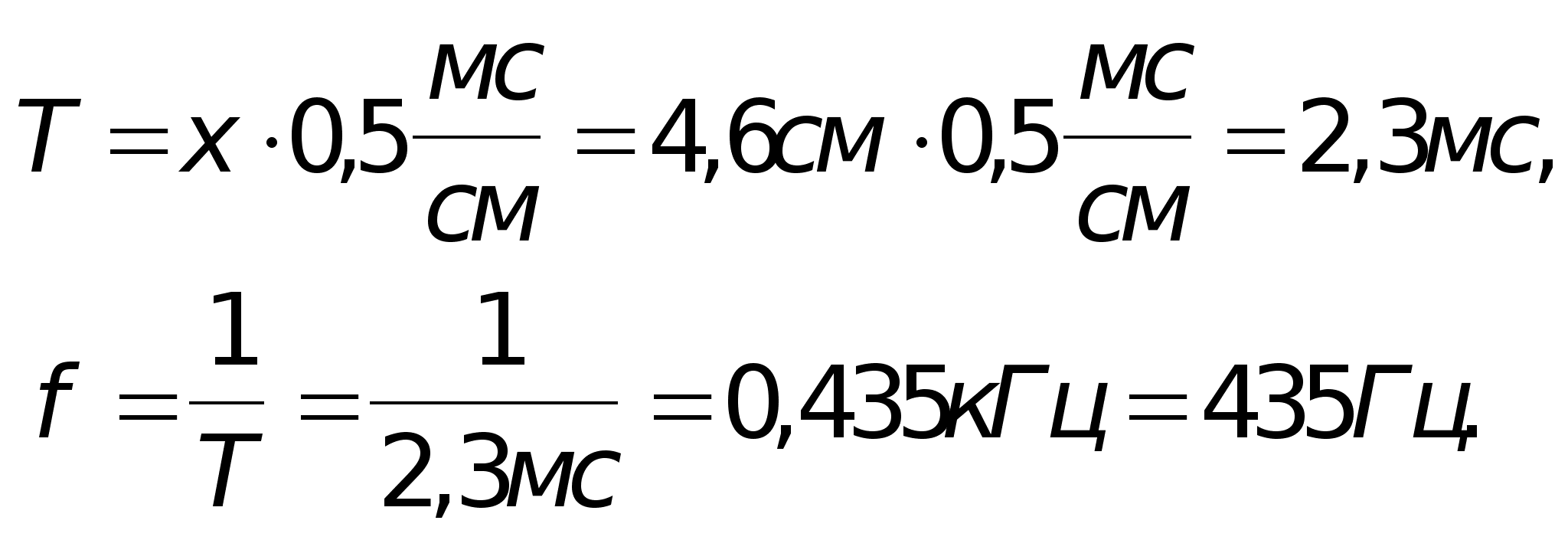
Полученные результаты приблизительно совпадают с показаниями генератора.

Вывод: на этой работе мы ознакомились с основными характеристиками радиоизмерительных приборов, правилами их подключения к измеряемому объекту, методикой проведения измерений и оценкой их погрешностей.

4

НГТУ

Нижегородский Государственный Технический Университет.

Лабораторная работа по физике №2-24.

Экспериментальные исследования электростатических полей с помощью электролитической ванны

Выполнил студент

Группы 99 – ЭТУ

Наумов Антон Николаевич

Проверил:

Н. Новгород 2000г.

Цель работы: изучение метода моделирования электростатических полей в электролитической ванне и исследование их характеристик в пространстве между электродами различной формы.

Теоретическая часть.

Электростатическое поле - поле, создаваемое покоящимися электрическими зарядами.

Характеристиками этого поля являются напряженность и потенциал , которые связаны между собой следующим соотношением: .

В декартовой системе координат: 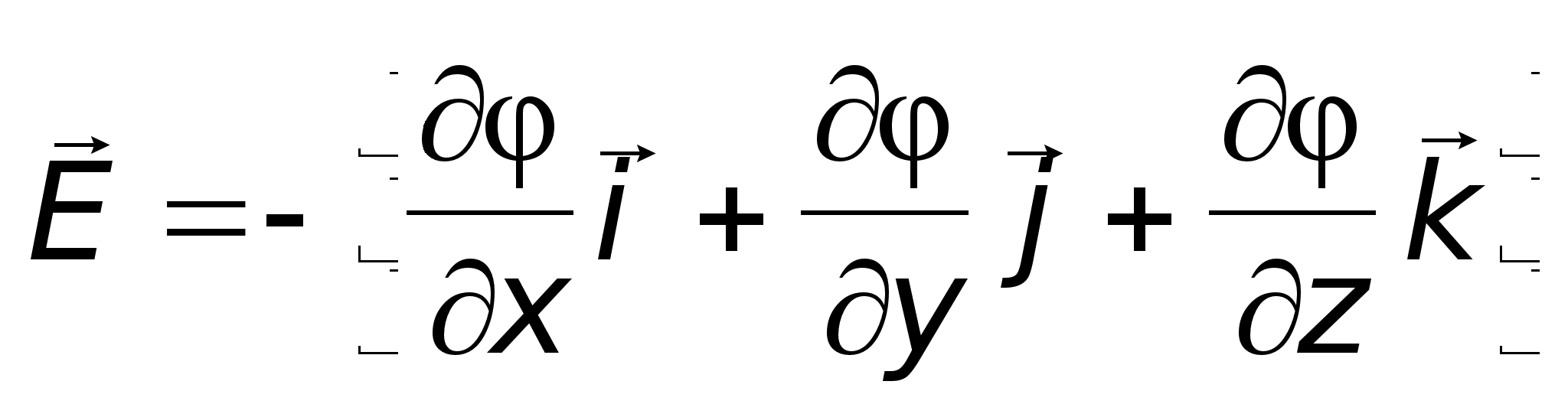, где единичные орты.

Удобной моделью электрического поля является его изображение в виде силовых и эквипотенциальных линий.

Силовая линия - линия, в любой точке которой направление касательной совпадает с направлением вектора напряженности

Эквипотенциальная поверхность - поверхность равного потенциала.

На практике электростатические поля в свободном пространстве создаются заданием на проводниках - электродах электрических потенциалов.

Потенциал в пространстве между проводниками удовлетворяет уравнению Лапласа:.

В декартовой системе координат оператор Лапласа: .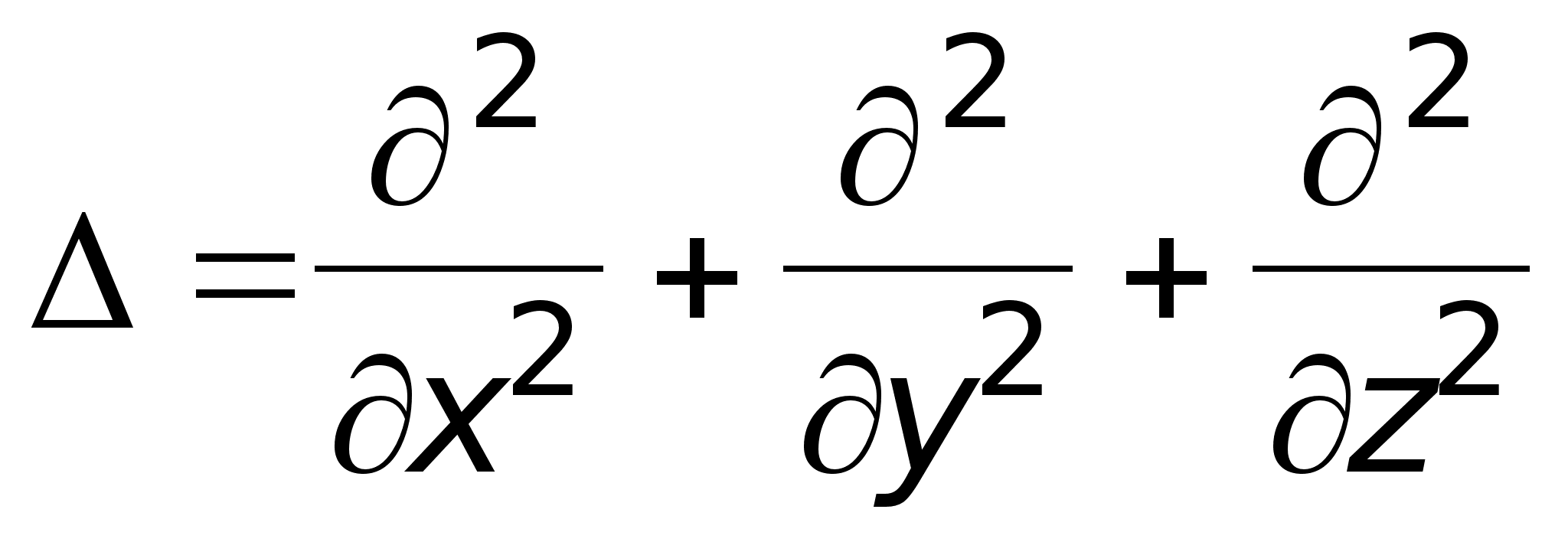

Решение уравнения Лапласа с граничными условиями на проводниках единственно и дает полную информацию о структуре поля.

Экспериментальная часть.

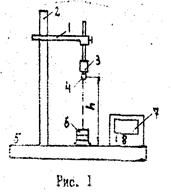
Схема экспериментальной установки.

Методика эксперимента:

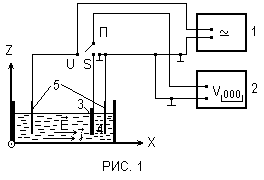
В эксперименте используются следующие приборы: генератор сигналов Г3 (I), вольтметр универсальный B7 (2) c зондом (3), электролитическая ванна (4) с набором электродов различной формы (5).

Устанавливаем в ванну с дистилированной водой электроды. Собираем схему, изображенную на РИС. 1. Ставим переключатель П в положение “U”. Подготавливаем к работе и включаем приборы. Подаем с генератора сигнал частоты f=5 кГц и напряжением U=5 В, затем ставим переключатель П в положение “S”. Далее, помещаем в ванну электроды различной формы ( в зависимости от задания ) и затем, водя по ванне зондом, определяем 4 - эквипотенциальные линии: 1B, 2B, 3B, 4B. И так далее для каждого задания.

Задание №1. Исследование электростатического поля плоского конденсатора.

Таблица 1. Зависимость потенциала  от расстояния.

 =  (x),В	x	y	 =  (x),В	x	y	 =  (x),В	x	y	 =  (x),В	x	y
0	-11	0	1,38	-5	0	2,88	1	0	4,34	7	0
0,14	-10	0	1,62	-4	0	3,13	2	0	4,57	8	0
0,37	-9	0	1,88	-3	0	3,40	3	0	4,8	9	0
0,62	-8	0	2,14	-2	0	3,65	4	0	4,99	10	0
0,82	-7	0	2,37	-1	0	3,88	5	0	4,99	11	0
0,1	-6	0	2,64	0	0	4,10	6	0

Таблица 2. Эквипотенциальные линии.

 =  (x),В	x	y	 =  (x),В	x	y	 =  (x),В	x	y	 =  (x),В	x	y
1	-5,7	9	2	-1,6	9	3	2,6	9	4	6,6	9
1	-5,8	6	2	-1,5	6	3	2,5	6	4	6,4	6
1	-5,7	3	2	-1,5	2	3	2,5	3	4	6,5	3
1	-5,7	0	2	-1,5	0	3	2,5	0	4	6,5	0
1	-5,7	-3	2	-1,5	-3	3	2,6	-3	4	6,5	-3
1	-5,7	-6	2	-1,5	-6	3	2,6	-6	4	6,5	-6
1	-5,8	-9	2	-1,5	-9	3	2,6	-9	4	6,5	-9

Обработка результатов измерений.

1). График зависимости .

2). Зависимость .

при x

при

при x>x₂

3). Погрешность измерения Е:

.

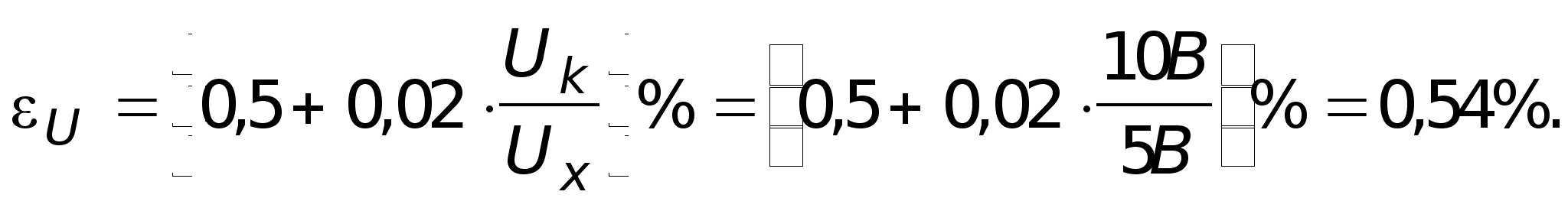
Е = (Е  Е) = (25  0,15)

4). Силовые и эквипотенциальные линии электростатического поля плоского конденсатора

5). Задача №1.

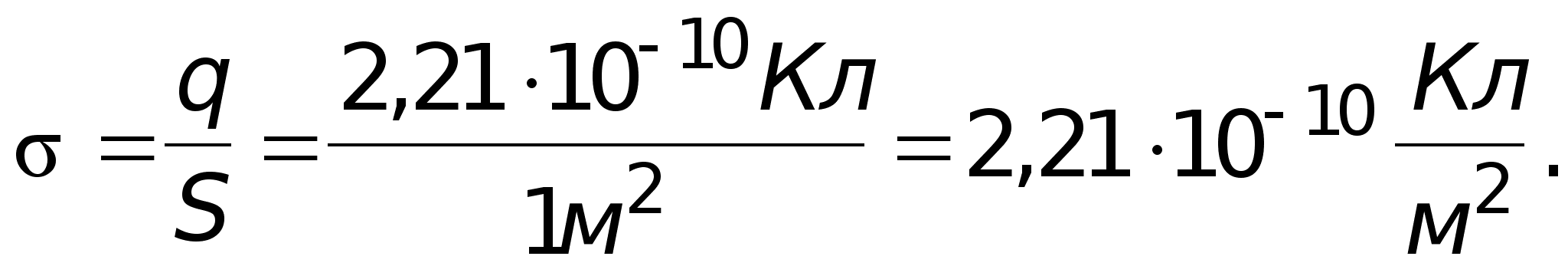
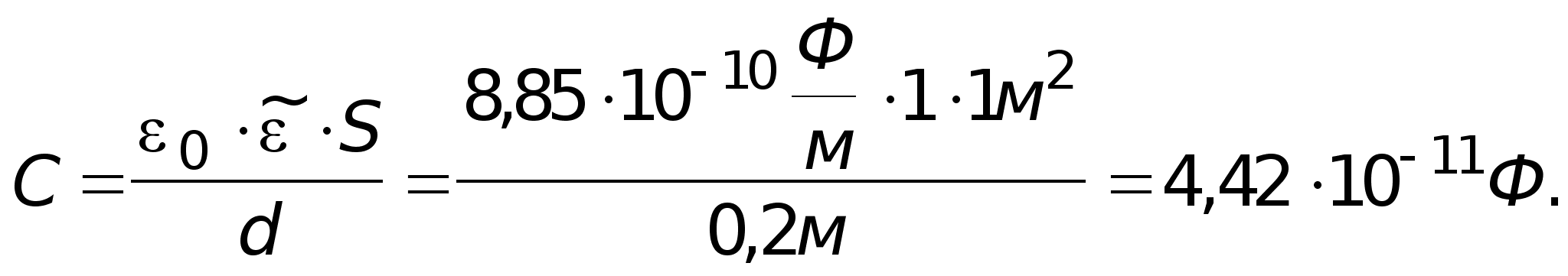
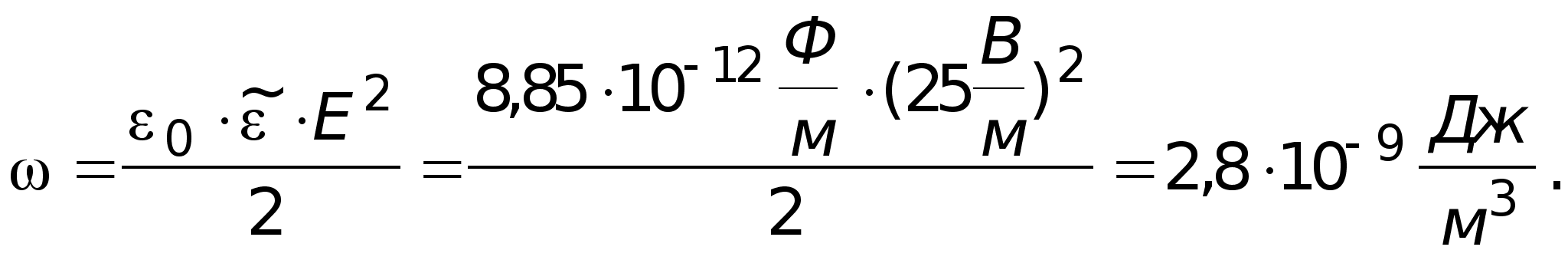
6). Задача №2.

;

Задание №2. Исследование электростатического поля цилиндрического конденсатора.

Радиусы цилиндров A =3,5 см, В=8,8см

Таблица 3. Зависимость

r),В	r,см	r),В	r,см
0,06	0	2,84	6
0,05	1	3,65	7
0,05	2	4,32	8
0,05	3	4,85	9
0,82	4	4,86	10
1,96	5

Таблица 4. Эквипотенциальные линии.

(x,y)	x	y	(x,y)	x	y	(x,y)	x	y	(x,y)	x	y
1	4	0	2	4,9	0	3	6,2	0	4	7,4	0
1	3,5	2	2	4,6	2	3	5,5	3	4	6,9	3
1	2,6	3	2	3	4	3	3,6	5	4	4,5	6
1	0	3,9	2	0	5	3	0	6,2	4	0	7,6
1	-2,6	3	2	-3,1	4	3	-3,7	5	4	-7	3
1	-3,6	2	2	-4,7	2	3	-5,5	3	4	-4,7	6
1	-4,2	0	2	-5,1	0	3	-6,3	0	4	-7,6	0
1	-3,7	-2	2	-4,8	-2	3	-5,3	-3	4	-6,8	-3
1	-2,9	-3	2	-3,2	-4	3	-3,6	-5	4	-4	-6
1	0	-4	2	0	-5,1	3	0	-6,2	4	0	-7,5
1	2,8	-3	2	-3	-4	3	3,6	-5	4	4,1	-6
1	3,6	-2	2	-4,7	-2	3	5,5	-3	4	7	-3

1). График зависимости r)

2). График зависимости ln r)

3). График зависимости E = E (r).

4). График зависимости E = E (1/r).

5). Эквипотенциальные линии.

6). Расчет линейной плотности  на электроде.

7). Задача №1.

L = 1м

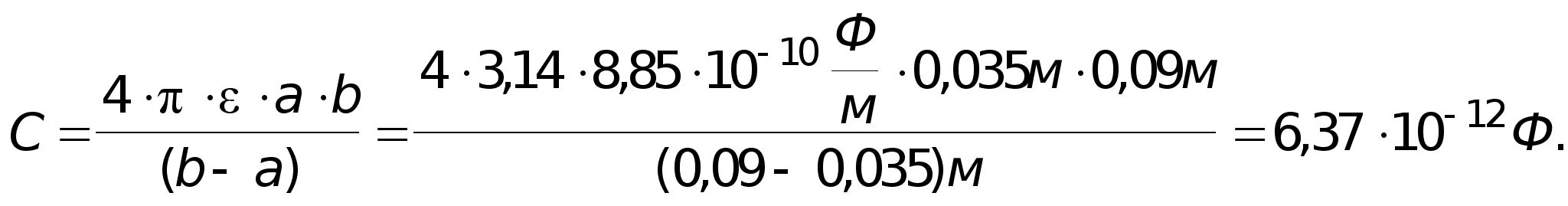
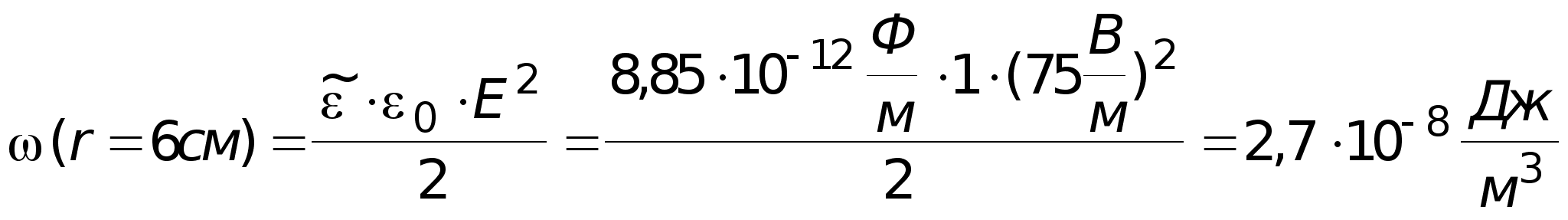
8). Задача №2.

r₁ = 5см, r₂ = 8см, l = 0,1м

Задание №3. Исследование электростатического поля вокруг проводников.

Таблица №5.

(x,y)	x	y	(x,y)	x	y	(x,y)	x	y	(x,y)	x	y
1	-3,6	8	2	0,8	8	3	5,9	9	4	7,2	3
1	-3,7	7	2	0,7	7	3	5,7	8	4	5,9	2
1	-3,7	6	2	0,5	6	3	5,2	7	4	5,4	1
1	-4	5	2	0,3	5	3	4,7	6	4	5,2	0
1	-4,7	4	2	0,2	4	3	4,4	5	4	5,4	-1
1	-5	3	2	0,1	3	3	4,1	4	4	6,2	-2
1	-5,2	2	2	0,6	-3	3	3,9	3	4	7,6	-3
1	-5,2	1	2	0,7	-4	3	3,8	2
1	-5	0	2	1	-5	3	4,1	-2
1	-4,9	-1	2	1,2	-6	3	4,4	-3
1	-4,7	-2	2	1,4	-7	3	4,8	-4
1	-4,4	-3	2	1,5	-8	3	5,5	-5
1	-4,2	-4	2	1,6	-9	3	6	-6
1	-4	-5				3	6,7	-7
1	-3,7	-6				3	7,3	-8
1	-3,6	-7				3	7,7	-9

1). Потенциал на электродах: пластинке и втулке постоянен, то есть они являются эквипотенциальными поверхностями. Внутри полости потенциал также постоянен.

Таблица 6.

(x,y)	x	y
1,97	-3	0
1,95	3	0
1,96	2	-1
1,95	-3	-2
1,95	0	0
1,96	-1	0

2). Распределение потенциала вдоль линии, охватывающей пластинку и расположенной на расстоянии

L = 3 мм от её края.

Таблица 7.

(x,y)	x	y
3,05	4	0
1,2	-4,2	0
1,92	0	-2,5
1,99	0	2
1,5	-3	2,1
1,31	-3	-3
2,23	2	-2
2,3	2	15

3). Эквипотенциальные линии.

4). Определение средней напряженности поля в нескольких точках вдоль силовой линии.

.

а).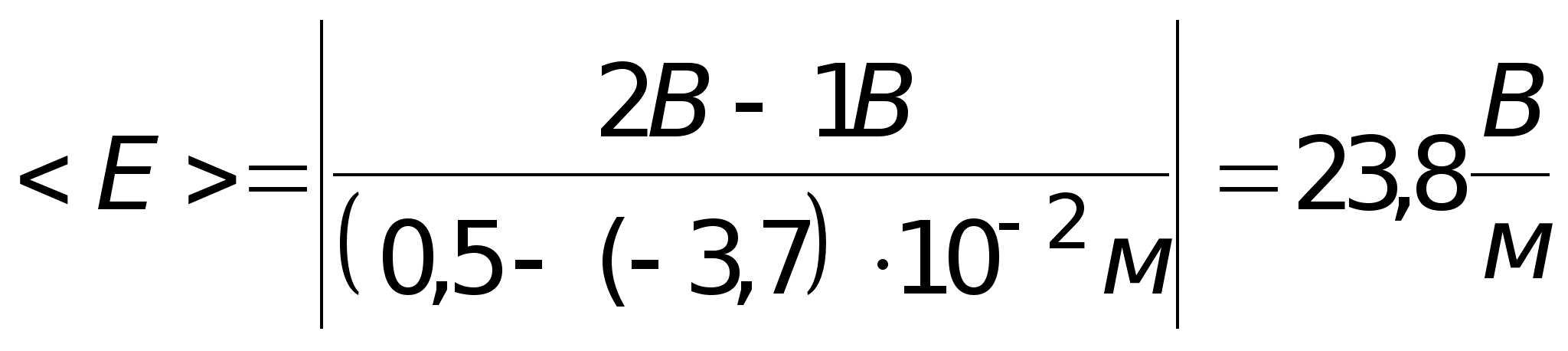

б).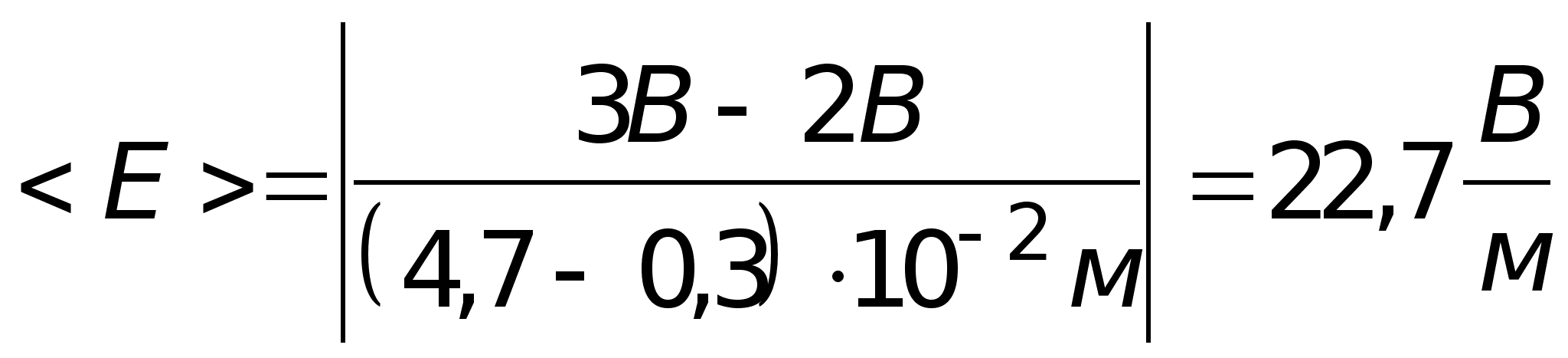

в).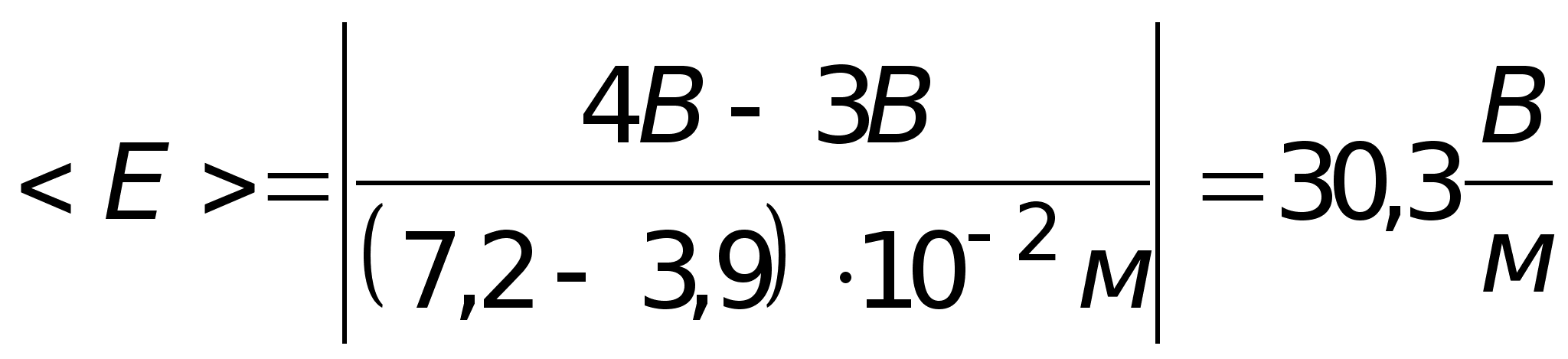

5). , .

Таблица 8.

X, см	y, см	, Кл/м2	E, В/м	, Дж/м3
4	0	3,2410-9	366,6	5,9510-7
-4,2	0	2,2110-9	250	2,7710-7
0	-5	8,8510-11	10	4,4310-10
0	2	1,1810-10	13,3	7,8210-10
-3	2,7	1,3310-9	150	9,9610-8
-3	-3	1,910-9	213	2,0010-7
2	-2	8,2310-10	93	3,8010-8
2	1,5	1,0210-9	116	5,9510-8

Вывод. В ходе работы получены картины силовых и эквипотенциальных линий плоском и цилиндрическом конденсаторах, а также вокруг проводника, помещенного в электростатическое поле. Установлено, что проводники и полости внутри них в электростатическом поле являются эквипотенциальными поверхностями.

В плоском конденсаторе поле сосредоточено между пластинами, оно является однородным, а потенциал изменяется линейно.

В цилиндрическом конденсаторе поле также сосредоточено между пластинами, его напряженность обратно пропорциональна расстоянию от оси конденсатора до точки измерения. Потенциал изменяется логарифмически.

Поток вектора напряженности поля через коаксиальные с электродами цилиндрические поверхности постоянен, что совпадает с теоретическими предположениями (теорема Гаусса).

11

НГТУ

Нижегородский Государственный Технический Университет.

Лабораторная работа по физике № 2-26.

Исследования магнитных полей в веществе.

Выполнил студент

Группы 99 – ЭТУ

Наумов Антон Николаевич

Проверил:

Н. Новгород 2000г.

Цель работы: получение зависимостей индукции магнитного поля, намагниченности и магнитной проницаемости ферромагнетика от напряженности магнитного поля; наблюдение петли гистерезиса для различных ферромагнетиков; изучение магнитных цепей.

Практическая ценность работы: экспериментально изучаются важнейшие свойства ферромагнетиков наличных марок: НМ 3000, НМ 600, ППГ (прямоугольная петля гистерезиса).

Теоретическая часть.

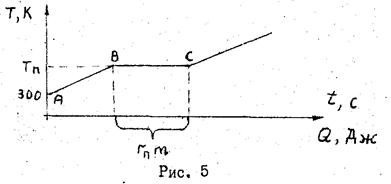
Опыт 1. Снятие основной кривой намагничивания (ОКН) ферромагнетика.

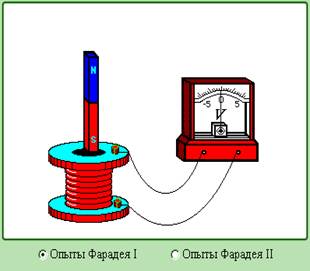
Схема экспериментальной установки.

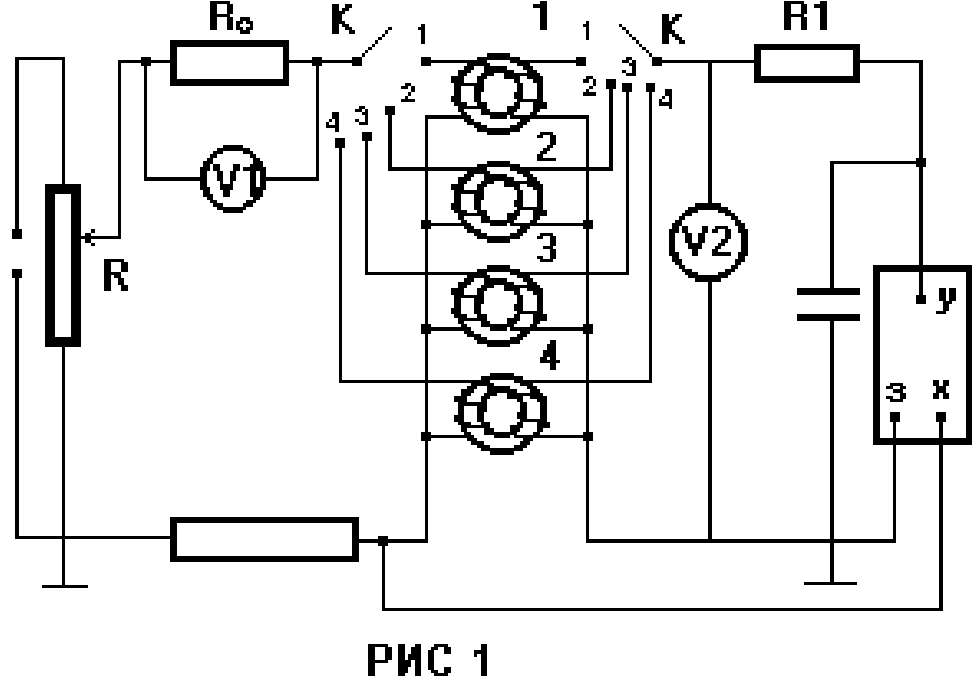
Cобрали цепь по схеме, показанной на РИС. 1. Для этого вольтметры V1 и V2 подключили к клеммам A-B и С-D - на верхней крышке макета соответственно. Переключатель К поставили в позицию 1. При этом исследовали трансформатор, кольцевой сердечник которого выполнен из ферита марки НМ 600, сопротивление R0=1 Ом. Таким образом, показания вольтметров численно равны: V1 - эффективному значению тока, текущего в текущей обмотке исследуемого трансформатора; V2 - эффективному значению ЭДС во вторичной обмотке. С помощью движка потенциометра R установили ток равный 0,5 А и плавно уменьшили его до нуля. Сняли показания вольтметров V1 и V2.

Данные для расчетов:

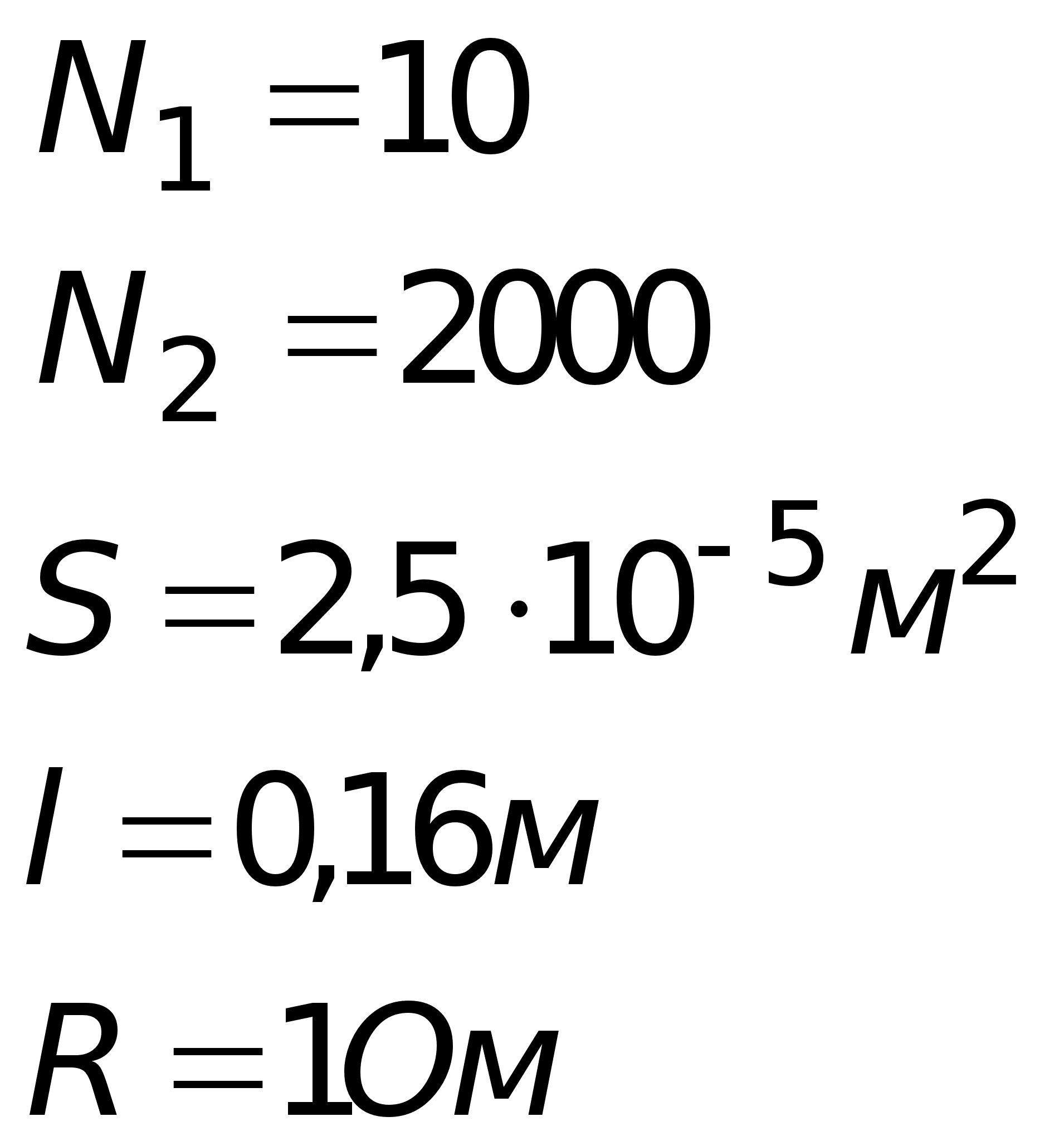
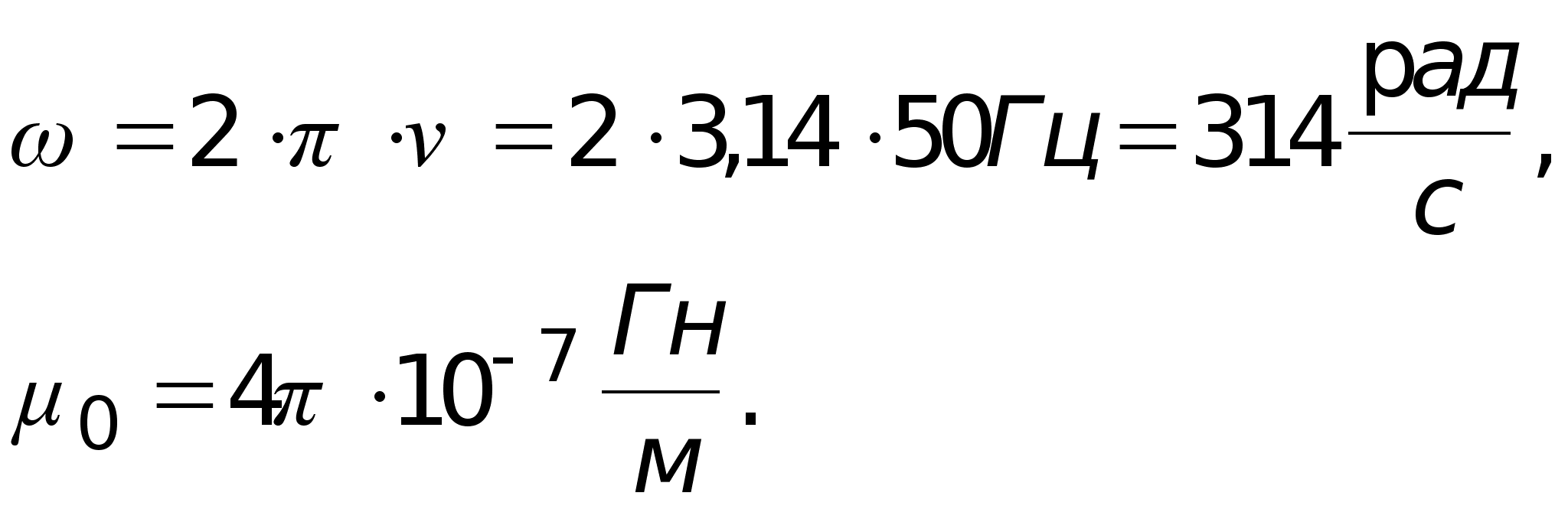
Используемые формулы:

Таблица № 1. Результаты расчетов.

№	U1, В	2, В	Im, А	m, В	Hm,А/м	Вm102,Тл	Jm10-3,А/м	102
1	0,04	0,01	0,06	0,02	3,75	0,1	0,78	2,1
2	0,10	0,18	0,14	0,25	8,75	1,6	12,77	14,6
3	0,14	0,34	0,20	0,48	12,50	3,1	24,61	19,7
4	0,21	0,73	0,30	1,03	18,75	6,6	52,50	28,0
5	0,29	1,13	0,41	1,60	25,63	10,2	81,25	31,7
6	0,36	1,42	0,51	2,01	31,88	12,8	102,02	32,0
7	0,40	1,57	0,57	2,22	35,63	14,1	112,23	31,5
8	0,48	1,79	0,68	2,53	42,50	16,1	127,93	30,1
9	0,54	1,91	0,76	2,70	47,50	17,2	136,80	28,8
10	0,59	1,99	0,83	2,81	51,86	17,9	142,62	27,5
11	0,65	2,10	0,92	2,97	57,50	18,9	150,08	26,1
12	0,70	2,14	0,99	3,03	61,88	19,3	153,46	24,8
13	0,76	2,22	1,07	3,14	66,88	20,0	159,17	23,8
14	0,84	2,29	1,19	3,24	74,38	20,6	164,38	22,1
15	0,90	2,33	1,27	3,30	79,38	21,0	167,49	21,1
16	0,95	2,36	1,34	3,34	83,75	21,3	169,18	20,2
17	1,00	2,40	1,41	3,39	88,13	21,6	171,85	19,5

Опыт 2. Наблюдение петли гистерезиса.

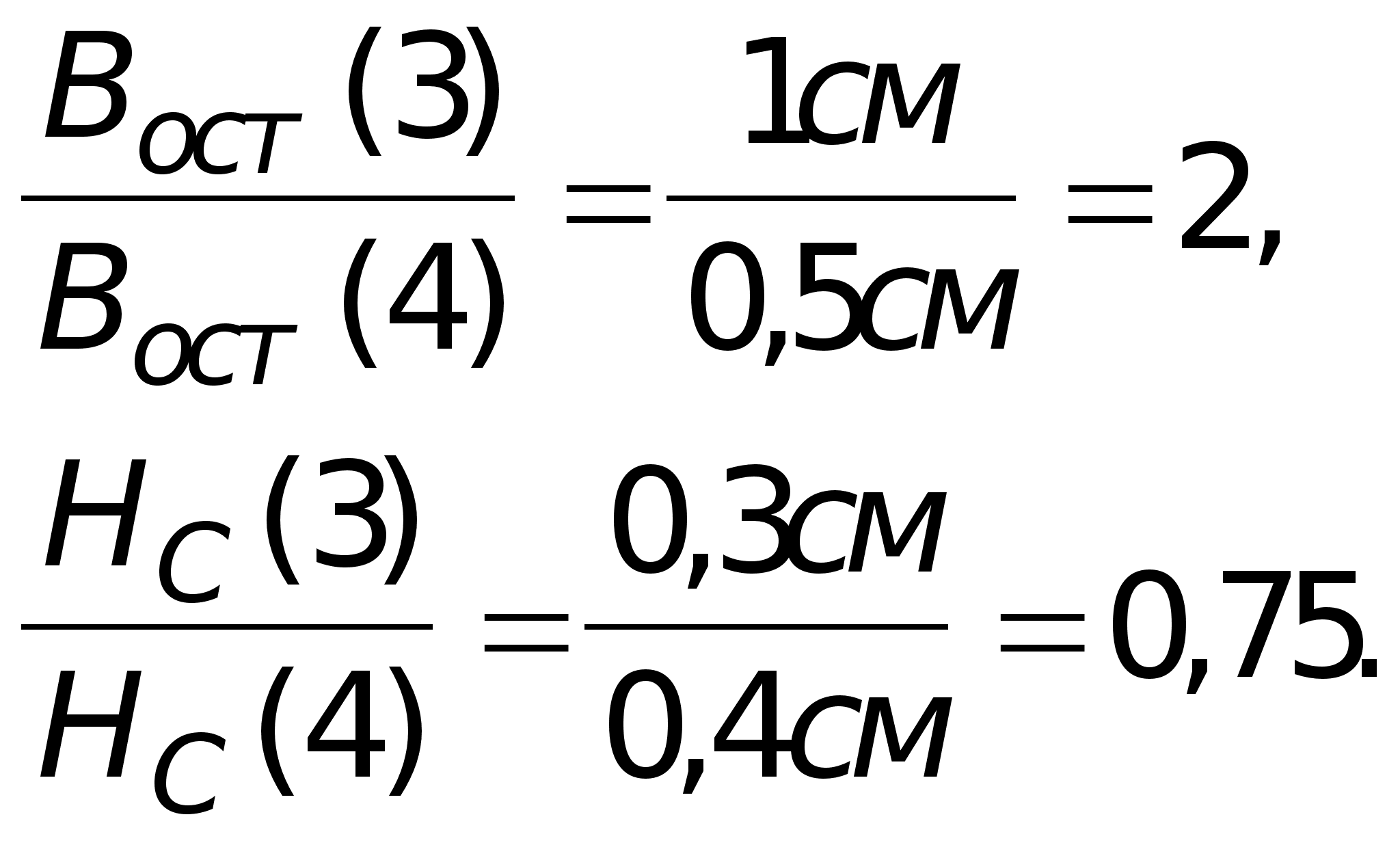
Для изготовления постоянного магнита лучше использовать ППГ, так как его коэрцитивная сила больше, чем у НМ-3000, а поэтому его сложней размагнитить.

Для изготовления сердечника силового трансформатора лучше взять ферромагнетик с меньшей коэрцитивной силой, чтобы снизить затраты на его перемагничивание.

Опыт 3. Исследование сердечника с зазором.

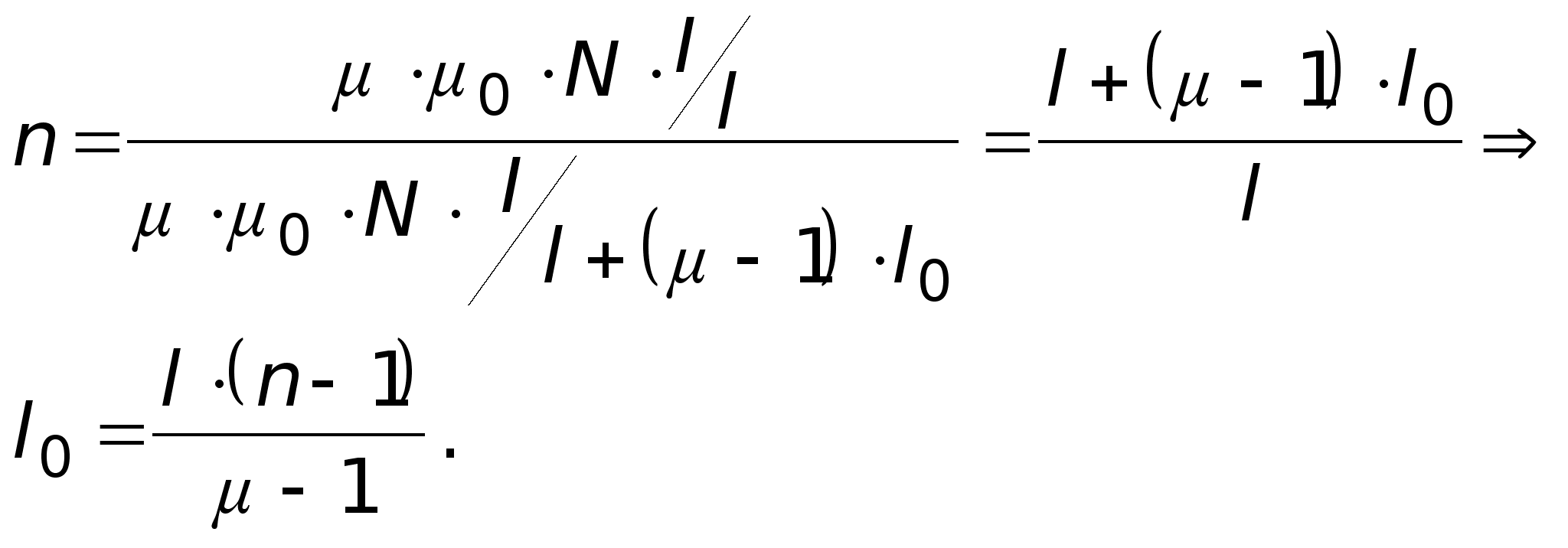
Графики.

График зависимости В=В(Н) График зависимости =(Н)

График зависимости J=J(H)

Вывод: на этой работе мы получили зависимости индукции магнитного поля, намагниченности и магнитной проницаемости ферромагнетика от напряженности магнитного поля; наблюдали за петлей гистерезиса для различных ферромагнетиков; изучили магнитные цепи.

4

НГТУ

Нижегородский Государственный Технический Университет.

Лабораторная работа по физике №2-27.

Исследование электрических колебаний.

Выполнил студент

Группы 99 – ЭТУ

Наумов Антон Николаевич

Проверил:

Н. Новгород 2000г.

Цель работы: экспериментальное исследование собственных и вынужденных колебаний тока и напряжения на элементах в колебательном контуре; измерение параметров контура: индуктивности L, сопротивления R, добротности Q; исследование прохождения синусоидального тока через LCR-цепь.

Теоретическая часть.

Рисунок 1.

Уравнение, которому удовлетворяет ток I в колебательном контуре (рис.1) с подключенным к нему генератором синусоидальной ЭДС =₀cost имеет вид: (1)

где:

- коэффициент затухания.

- собственная круговая частота, R - сопротивление резистора, L - индуктивность катушки, С - емкость конденсатора, ; ₀,  - амплитуда и круговая частота синусоидальной ЭДС.

Общее решение неоднородного линейного уравнения (1):

(2)

где: - круговая частота собственных затухающих колебаний тока.

и - начальные амплитуда и фаза собственных колебаний.

I₀ - амплитуда вынужденных колебаний тока.

 - разность фаз между ЭДС и током.

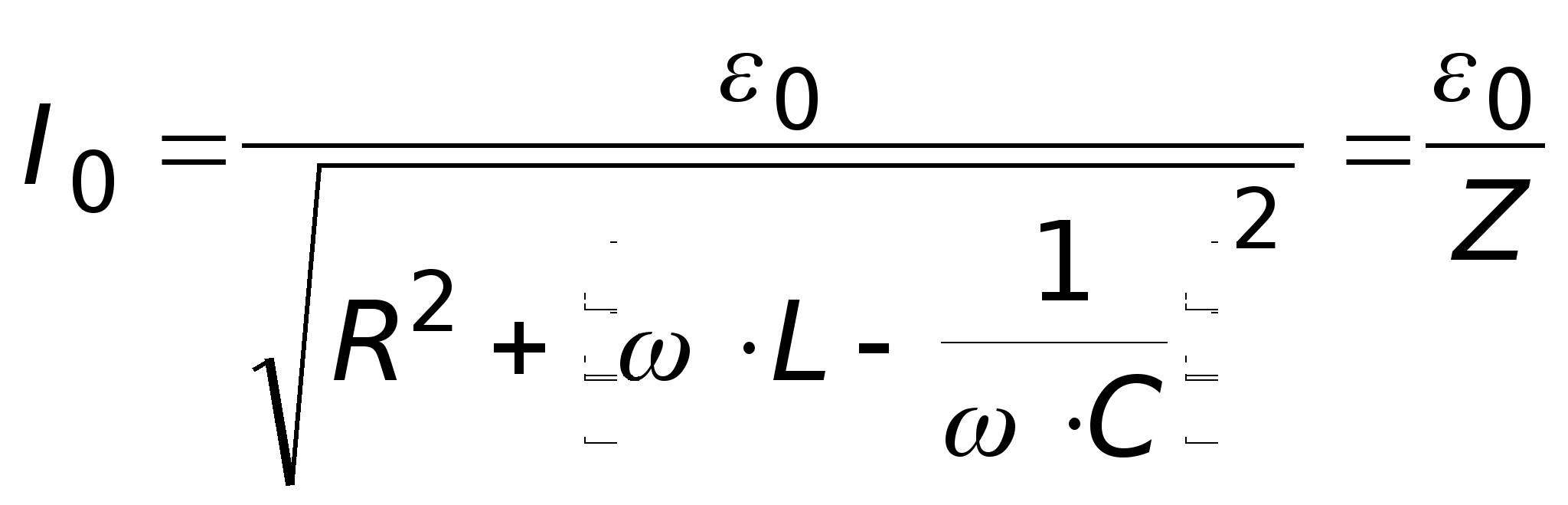(3)

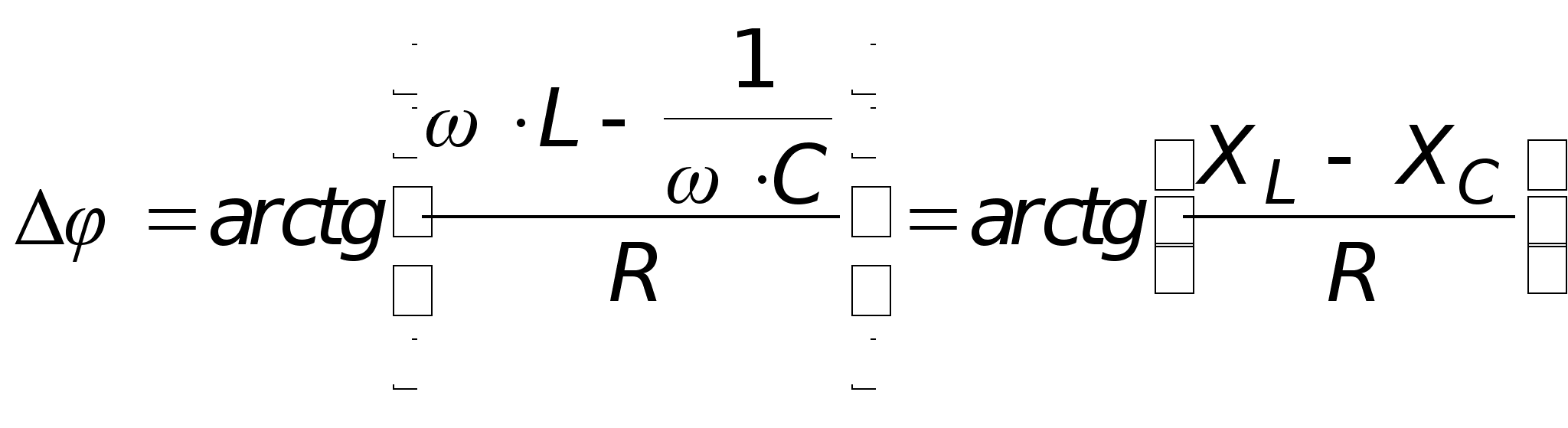(4)

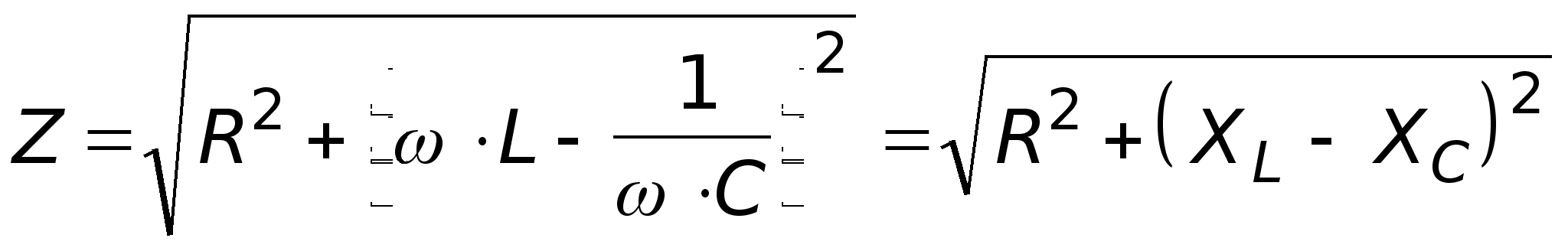- импеданс цепи.

- индуктивное сопротивление, - емкостное сопротивление.

Собственные колебания:

Если ²