Нахождения равновесной в модели Эрроу-Гурвица

Реферат №4 по Экономико-Математическому Моделированию

Студент группы М-2-4 Иванников Сергей

Научный руководитель Бабешко Л.О.

Москва 1996 Вариант №8 Односторонняя модель Эрроу-Гурвица

Здесь будет рассмотрена модель, в которой в виде участвующих субъектов участвуют:

1.

Два предприятия, использующие один и тот же ресурс (труд L) и производящие один и тот же вид продукции Y.

Производственная функция здесь имеет вид:

где

- спрос на труд со стороны предприятия i

- параметры производственной функции.

2.

Функция полезности с точки зрения потребителей имеет вид:

Потребители стремятся максимизировать функцию полезности, производители - функцию прибыли, выражаемую следующей формулой:

где - цена производимого продукта

- объем выпуска фирмы i

- цена ресурса (труда)

В модели рассматривается рынок совершенной (абсолютной) конкуренции.

Исходные данные модели Эрроу-Гурвица

- цена на продукцию в предшествующем периоде,

- цена на ресурс в предшествующем периоде,

- предложение труда

- спрос предшествующего периода на продукцию фирмы i,

- параметры функции полезности и производственной функции

- коэффициент корректировки цен.

Реакция предприятия на цены

А. - размер спроса на ресурсы

Б. - размер предложения продукта

Реакция потребителей на цены

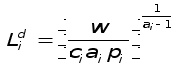
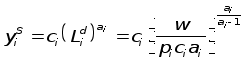
Потребитель определяет объем спроса пропорционально разнице между предельной полезностью и предельными затратами:

;

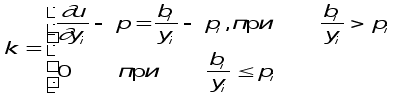
- коэффициент пропорциональности, ускоряющий процесс сходимости итераций.

- избыточный спрос на продукт

- избыточный спрос на ресурс

Корректировка цен:

Если , то цены увеличиваются,

если , то цены падают,

если , то цены не меняются - система в состоянии равновесия

Практический пример Исходные данные модели Эрроу-Гурвица

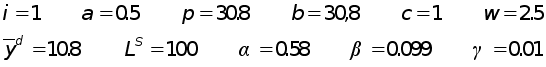
Необходимо определить состояние равновесия с точностью 1,5

Реакция предприятия на цены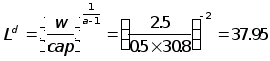

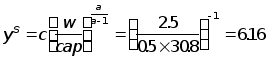
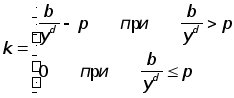
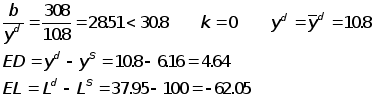
Реакция потребителя на цены

Равновесие не достигнуто, так как избыточный спрос спревышает требуемую величину в 1,5. Цена возрастает.

Проведем интерацию №1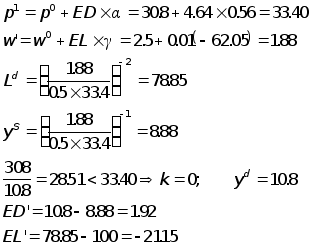

Равновесие не достигнуто

Проведем интерацию №2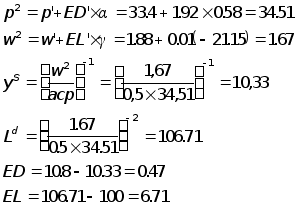

- равновесие достигнуто с заданной точностью

Результат:

Интерации	P	W	Ld	yS	yd	ED
-	30.8	2.5	37.95	6.16	10.8	4.64
1	33.4	1.88	78.85	8.88	10.8	1.92
2	34.51	1.67	106.71	10.33	10.8	0.47

Равновесие было достигнуто после проведения второй интерации.

В работе использовались лекции по ЭММ доцента Л.О.Бабеш