Л.О. Бабешко, доцент кафедры "Математическое моделирование экономических процессов"
АннотацияДанная работа посвящена вопросу прогнозирования характеристик основных финансовых инструментов фондового рынка при помощи модели средней квадратической коллокации (* Термин "коллокация" (англ. collocation - взаиморасположение; расстановка) после пуб-ликации работы советского математика и экономиста Л.В. Канторовича "Об одном мето-де приближенного решения дифференциальных уравнений в частных производных" (1934) широко используется в современной вычислительной математике для прибли-женного решения дифференциальных уравнений. Под коллокацией, с математической точки зрения, понимается определение функции путем подбора аналитической аппрок-симации к определенному числу заданных линейных функционалов. "Математическая" ("чистая") коллокация нашла широкое применение в технических приложениях при ре-шении интерполяционных задач. Дальнейшее обобщение теории коллокации связано с применением к объектам стохастической природы и вслед за работами Г. Морица (на-пример: Moritz H. Least-Squares Collocation // Reviews of Geophysics and Space Physics. V. 16. No. 3. Aug. 1978. P. 421-430) под коллокацией понимается обобщение метода наименьших квадратов на случай бесконечномерных гильбертовых пространств.). Коллокационная модель прогнозирования сохраняет основные преимущества классических регрессионных моделей - инвариантность по отношению к линейным преобразованиям исходных данных и результатов, оптимальность решения (в смысле наиболее точного прогноза из всех возможных вариантов линейных решений на основе заданных исходных данных) - и имеет дополнительные достоинства: результат не зависит от числа оцениваемых величин; как наблюдаемые, так и оцениваемые величины могут быть разнородными (иметь различную физическую, экономическую или математическую природу). Коллокационная модель может быть использована не только для построения оптимального прогноза однородных данных, но и для оценивания любых интересующих характеристик финансовых инструментов фондового рынка по неоднородной исходной информации (доходностей, курсов, объемов продаж, индексов и т.д.).
Потребность в прогнозировании как специфическом научно-прикладном анализе (нацеленном на будущее или учитывающем неопределенность, связанную с отсутствием или неполнотой информации) возникает со стороны самых разнообразных областей человеческой деятельности – политики, международных отношений, экономики, финансов и т.д.
Предвидение вероятного исхода событий дает возможность заблаговременно подготовиться к ним, учесть их положительные и отрицательные последствия, а если это возможно – вмешаться в ход развития, что особенно важно в финансовой сфере, подверженной различного рода рискам.
В общем виде задачу прогнозирования можно сформулировать следующим образом: по имеющейся информации X (измерениям, наблюдениям) требуется предсказать (спрогнозировать, оценить) некоторую величину Y, стохастически связанную с X. Например, по имеющейся информации о динамике цен на ту или иную ценную бумагу оценить ее значение на какой-то период в будущем или оценить доходность одних ценных бумаг, используя информацию о доходности других ценных бумаг, и т.д.
Искомое значение Y можно оценить различными способами, но в любом случае это приближенное значение будет базироваться лишь на исходной информации:
![]() .
.
Различные функции определяют различные методики прогноза оценки Y. Ниже мы рассмотрим методику линейного стохастического прогнозирования.
Итак, пусть имеется два множества случайных величин: множество значений независимой переменной (измерений) ![]() , образующих n-мерный вектор-столбец, и множество значений зависимой переменной (сигналов)
, образующих n-мерный вектор-столбец, и множество значений зависимой переменной (сигналов) ![]() , образующих m-мерный вектор-столбец (значок ( ) – означает транспонирование).
, образующих m-мерный вектор-столбец (значок ( ) – означает транспонирование).
Предполагается, что каждая из переменных является центрированной случайной величиной, т.е. имеет математическое ожидание равное нулю:
E{X} = 0, E{Y} = 0. (1)
Если это не так, то выполняется центрировка, то есть значения E{X} 0 и E{X} 0 вычитаются из заданных значений переменных X и Y соответственно.
Пусть имеется дополнительная информация в виде ковариационных функций:
1) автоковариационных функций векторов X и Y,
![]() (2)
(2)
![]() (3)
(3)
где Xj = X(tj) – значение переменной в момент tj, j=1, … , n,
Yk = Y(tk) – значение переменной в момент tk, k=1, … , m,
– интервал времени между соответствующими моментами;
2) взаимных ковариационных функций между X и Y
![]()
![]() (4)
(4)
По данным ковариационным функциям для различных интервалов можно составить соответствующие ковариационные матрицы:
![]() ,
, ![]() ,
, ![]() ,
, ![]() . (4)
. (4)
Предполагается, что данные ковариационные матрицы имеют полный ранг, т.е. ранг равный наименьшему из чисел m и n.
Задача состоит в оценке вектора Y по измеренным значениям вектора X. Причем связь между векторами будет определяться не через функциональное соотношение, а только через ковариационные матрицы (4) .
Ограничиваясь методикой линейного прогноза, будем искать оценку вектора Y в виде
![]() , (5)
, (5)
или в координатной форме:
![]() , i=1, …, m,
, i=1, …, m,
т.е. каждый элемент вектора Y аппроксимируется линейной комбинацией исходных данных X = (X1, X2, ..., Xn)'.
Ошибка аппроксимации (вектор ошибок) определяется как разность между истинным значением переменной и оценкой
= Y – ![]() . (6)
. (6)
Ковариационная матрица и дисперсии ошибок определяются по формулам
![]() , (7)
, (7)
![]() (8)
(8)
соответственно. Согласно общей теории статистического оценивания наилучшая (оптимальная) линейная оценка определяется как несмещенная линейная оценка с минимальной дисперсией. Несмещенность линейной оценки (5) проверяется непосредственно
![]() ,
,
с учетом (1) и свойств математического ожидания.
Для того чтобы дисперсия линейной оценки (5) была минимальной, матрица H должна определяться из следующих соображений.
Ковариационная матрица ошибок для произвольной матрицы H имеет вид:
![]()
![]() .
.
Вычитая из правой части квадратичную форму ![]() и добавляя ее, а также домножая члены
и добавляя ее, а также домножая члены ![]() на единичную матрицу E =
на единичную матрицу E = ![]() , можно представить ковариационную матрицу ошибок в виде суммы двух матриц:
, можно представить ковариационную матрицу ошибок в виде суммы двух матриц:
![]() =
=![]() –
–![]() +
+![]() +
+![]() =
=
=![]() ,
,
где A = ![]() , B =
, B = ![]() .
.
Матрица А одинакова для всех линейных оценок, так как она не зависит от матрицы H. Заметим, что элементы матрицы В являются неотрицательными числами (поскольку ковариационная матрица Kxx является невырожденной, а как известно, все невырожденные ковариационные матрицы положительно определены), поэтому диагональные элементы матрицы K , представляющие собой дисперсии ошибок, будут наименьшими только в том случае, когда матрица В является нулевой
B = ![]() = 0. (9)
= 0. (9)
Отсюда следует, что дисперсии ошибок будут минимальными, если матрица Н определяется выражением
![]() . (10)
. (10)
Таким образом, выражение для оптимальной (несмещенной, с минимальной дисперсией) линейной оценки получается подстановкой в формулу (5) выражения (10):
![]() . (11)
. (11)
При этом ковариационная матрица ошибок прогнозирования переменной Y с учетом (9) принимает вид
K = KYY – ![]() . (12)
. (12)
При практической реализации алгоритма прогнозирования (11) целесообразно сначала вычислить вектор C
C = ![]() , (13)
, (13)
поскольку сомножители в данном выражении не зависят от значений переменной Y, а затем выполнять умножение на матрицу взаимных ковариаций
![]() .
.
Если выполняется прогноз одного значения переменной Y, например на момент t = p,![]() , то вектор C умножается на вектор-строку ковариаций
, то вектор C умножается на вектор-строку ковариаций
![]() ,
,
где ![]() ,
,![]() ,
,
![]() . (14)
. (14)
Данный метод может быть использован при прогнозировании значений переменных как по пространственным данным (пространственный срез) (cross-sectional data), например, по набору сведений о доходностях разных ценных бумаг (X и Y) за один и тот же период (момент) времени, так и по данным временных рядов (time-series data), например, доходности ценной бумаги данного вида (Y) за несколько лет.
Во втором случае, т.е. в случае, когда прогноз ![]() переменной Y в момент t = p выполняется по данным временного ряда
переменной Y в момент t = p выполняется по данным временного ряда ![]() , формула (11) принимает следующий вид
, формула (11) принимает следующий вид
![]() , (14')
, (14')
где![]() – вектор-строка ковариаций, с элементами
– вектор-строка ковариаций, с элементами ![]() (i=1, …, m); KYY – автоковариационная матрица вектора Y.
(i=1, …, m); KYY – автоковариационная матрица вектора Y.
При этом формулу для дисперсии ошибки прогноза в момент t = p (с учетом выражения (12)) можно переписать следующим образом
![]() , (15)
, (15)
где Dy – дисперсия случайного процесса Y.
Поскольку ковариационная матрица положительно определена и, следовательно, квадратичная форма ![]() в выражении (15) принимает неотрицательные значения, любой прогноз будет уменьшать исходную дисперсию Dy. В худшем случае, когда точка p, в которой выполняется прогноз, настолько удалена от ординат Yi, i=1, 2, …, m с заданными значениями, что вектор ковариаций
в выражении (15) принимает неотрицательные значения, любой прогноз будет уменьшать исходную дисперсию Dy. В худшем случае, когда точка p, в которой выполняется прогноз, настолько удалена от ординат Yi, i=1, 2, …, m с заданными значениями, что вектор ковариаций ![]() является нулевым вектором, дисперсия прогноза будет равна дисперсии исходного процесса Dy:
является нулевым вектором, дисперсия прогноза будет равна дисперсии исходного процесса Dy:
D (P) = Dy.
Если момент t = p, на который выполняется прогноз переменной Y, совпадает с моментом t = i, на который известно ее значение Yi, элементы вектора ковариаций ![]() будут совпадать с элементами i-й строки
будут совпадать с элементами i-й строки ![]() ' и элементами i-го столбца
' и элементами i-го столбца ![]() матрицы автоковариаций KYY. Поэтому в соответствии с (14) значение прогноза будет в точности совпадать с заданным значением переменной
матрицы автоковариаций KYY. Поэтому в соответствии с (14) значение прогноза будет в точности совпадать с заданным значением переменной
![]() , (16)
, (16)
и в соответствии с (15) ошибка дисперсии прогноза D (P) = 0, так как квадратичная форма![]() при p = i достигает своего максимального значения, равного дисперсии Dy.
при p = i достигает своего максимального значения, равного дисперсии Dy.
Формулы (10) и (14) называются средним квадратическим прогнозом или коллокацией [1] и представляют собой аналог формулы прогноза Колмогорова–Винера, известной из теории стохастических процессов. И как показано выше, вся методика линейного прогноза сводится к простейшим матричным операциям.
Используя данные временных рядов по годовым доходностям долгосрочных облигаций корпораций США и доходностям рыночного портфеля (портфеля, включающего акции 500 фирм и выбранного корпорацией Standard & Poor's для характеристики рынка в среднем) за период исследования (с 1984 по 1993 г.) [2], выполним сравнительный анализ результатов прогнозирования, полученных при помощи парной регрессионной модели и модели коллокации (табл. 1).
Таблица 1
| t | Год | Долгосрочные облигации корпораций Yt, % | Портфель обыкновенных акций Xt, % |
| 1 | 1984 | 16,39 | 6,27 |
| 2 | 1985 | 30,90 | 32,16 |
| 3 | 1986 | 19,85 | 18,47 |
| 4 | 1987 | -0,27 | 5,23 |
| 5 | 1988 | 10,70 | 16,81 |
| 6 | 1989 | 16,23 | 31,49 |
| 7 | 1990 | 6,78 | -3,17 |
| 8 | 1991 | 19,89 | 30,55 |
| 9 | 1992 | 9,39 | 7,67 |
| 10 | 1993 | 13,19 | 9,99 |
В качестве исходных данных будем использовать значения доходностей за девять лет (с 1984 по 1992 г. включительно), а последнее значение, соответствующее 1993 г., будем использовать для контроля качества прогноза, поэтому число данных n в обеих моделях будем принимать равным 9.
Регрессионная модель прогноза, с оцененными по методу наименьших квадратов параметрами, имеет вид:
![]() . (17)
. (17)
Для определения точностных характеристик модели (оценка дисперсии параметров модели, дисперсии прогноза и т.д.) вычисляются остатки регрессии ![]() и находится сумма их квадратов (табл. 2).
и находится сумма их квадратов (табл. 2).
Таблица 2
| t | Yt |
| et |
|
| 1 | 16,39 | 9,277 | 7,113 | 50,598 |
| 2 | 30,90 | 22,758 | 8,142 | 66,293 |
| 3 | 19,85 | 15,629 | 4,221 | 17,813 |
| 4 | -0,27 | 8,735 | -9,005 | 81,094 |
| 5 | 10,70 | 14,765 | -4,065 | 16,525 |
| 6 | 16,23 | 22,409 | -6,179 | 38,181 |
| 7 | 6,78 | 4,361 | 2,419 | 5,850 |
| 8 | 19,89 | 21,920 | -2,030 | 4,119 |
| 9 | 9,39 | 10,006 | -0,616 | 0,379 |
| | 280,853 |
Оценка дисперсии ошибок регрессии и оценки дисперсии параметров модели для данных табл. 2 соответственно равны: ![]() 40,122;
40,122; ![]() 0,0294;
0,0294; ![]() 12,128. Коэффициент детерминации R2, характеризующий качество подгонки регрессионной модели к наблюденным значениям Yt , (t = 1, …, 9) и F – статистика, используемая для проверки его значимости (R2=0,506, F=9,237 > F (k1, k2) = F (1,7) = 5,59, где F – критическое значение критерия при пятипроцентном уровне значимости = 5%, и уровней свободы k1 = 1 и k2 = n–2 = 7), свидетельствуют о том, что есть основания полагать, что между переменными имеется корреляционная зависимость.
12,128. Коэффициент детерминации R2, характеризующий качество подгонки регрессионной модели к наблюденным значениям Yt , (t = 1, …, 9) и F – статистика, используемая для проверки его значимости (R2=0,506, F=9,237 > F (k1, k2) = F (1,7) = 5,59, где F – критическое значение критерия при пятипроцентном уровне значимости = 5%, и уровней свободы k1 = 1 и k2 = n–2 = 7), свидетельствуют о том, что есть основания полагать, что между переменными имеется корреляционная зависимость.
При помощи регрессии (17) выполним прогноз доходности долгосрочных облигаций корпораций на 1993 г. Y93 по значению доходности рыночного портфеля на этот год X93=9,99:
![]() ,
,
и, таким образом, отклонение от истинного значения составляет
Y93 –![]() = 13,19 – 11,21 = 1,98, (18)
= 13,19 – 11,21 = 1,98, (18)
а оценка дисперсии прогноза индивидуального значения ![]() = 45,699.
= 45,699.
Теперь выполним прогноз, используя модель коллокации (11). Для этого необходимо построить модели ковариационных функций: автоковариационной функции вектора X, взаимной ковариационной функции между X и Y, взаимной ковариационной функции между Y и X.
Первым шагом при построении ковариационных функций является вычисление оценок ковариаций по данному динамическому ряду:
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
где ![]() – выборочные средние.
– выборочные средние.
Вторым шагом является выбор подходящей аппроксимирующей функции, и если нет каких-либо дополнительных соображений теоретического характера, то в качестве таковых обычно выбирают непрерывные функции вида:
![]() ,
,
![]() , (19)
, (19)
где , , K(0) = DY – параметры модели. Поскольку члены последовательностей ![]() ,
, ![]() ,
, ![]() , ( = 0, ..., k) для данных табл. 1 меняют знак, то в данной работе воспользуемся выражением (19).
, ( = 0, ..., k) для данных табл. 1 меняют знак, то в данной работе воспользуемся выражением (19).
На третьем шаге выполняется оценка параметров модели ковариационной функции (например, по методу наименьших квадратов). В данной работе воспользуемся методом, основанным на использовании "существенных" параметров:
1) дисперсии процесса K(0) = DY ;
2) радиуса корреляции 0,5 – значение аргумента ковариационной функции, при котором ее значение равно половине дисперсии, т.е.
K( 0,5) = ![]()
3) наименьшего положительного корня 0 уравнения: K( ) = 0. Связь параметров модели с существенными параметрами устанавливается следующим образом:
![]() , где = 3,14. (20)
, где = 3,14. (20)
![]() . (21)
. (21)
Значения существенных параметров и параметров моделей ковариационных функций представим в табл. 3.
Таблица 3
| Ковариационная | Существенные параметры | Параметры модели | ||
| функция | 0 | 0,5 | | |
| KXX( ) | 0,6193 | 0,3096 | 1,1193 | 2,5366 |
| KYY( ) | 1,0293 | 0,5054 | 0,7133 | 1,5261 |
| KYX( ) | 0,7417 | 0,3709 | 0,9345 | 2,1177 |
| KXY( ) | 0,6619 | 0,3310 | 1,0472 | 2,3731 |
По построенным ковариационным функциям, для различных интервалов ( = 0, ..., 9) между моментами ti, tj, i = 1, ..., 9, j = 1, …, 9 рассчитаем соответствующие ковариационные матрицы:
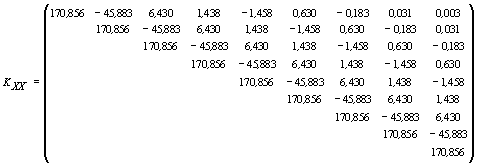

Обращая матрицу KXX и перемножая обратную матрицу ![]() на вектор центрированных значений переменной X, а затем, умножая произведение C =
на вектор центрированных значений переменной X, а затем, умножая произведение C =![]() X на матрицу KYX, получим центрированные значения прогнозов переменной Y на моменты
X на матрицу KYX, получим центрированные значения прогнозов переменной Y на моменты
t = 1, …, 9, соответствующие периоду исследования (с 1984 по 1992 г.). Добавляя к центрированным значениям прогнозов среднее по выборке ![]() и вычисляя отклонения прогнозов от истинных значений переменной, найдем сумму квадратов отклонений (табл. 4).
и вычисляя отклонения прогнозов от истинных значений переменной, найдем сумму квадратов отклонений (табл. 4).
Таблица 4
| t | Yt |
| et |
|
| 1 | 16,39 | 9,232 | 7,158 | 51,232 |
| 2 | 30,90 | 23,498 | 7,402 | 54,786 |
| 3 | 19,85 | 15,769 | 4,081 | 16,652 |
| 4 | -0,27 | 7,407 | -7,677 | 58,935 |
| 5 | 10,70 | 16,226 | -5,526 | 30,535 |
| 6 | 16,23 | 21,489 | -5,259 | 27,653 |
| 7 | 6,78 | 4,933 | 1,847 | 3,411 |
| 8 | 19,89 | 21,459 | -1,569 | 2,462 |
| 9 | 9,39 | 10,436 | -1,046 | 1,093 |
| | 246,760 |
Для прогнозирования доходности долгосрочных облигаций корпораций на 1993 г. Y93(t = 10) вектор значений ковариаций (14)
(-0,006 0,020 -0,036 -0,017 0,362 -1,346 2,578 0,370 -22,446),
вычисленный по моделям взаимных ковариационных функций ![]() (см. табл. 3), умножается на вектор C =
(см. табл. 3), умножается на вектор C =![]() X, в результате получается значение
X, в результате получается значение
![]() ,
,
и, таким образом, отклонение от истинного значения составляет
Y93 –![]() = 13,19 – 14,903 = -1,71.
= 13,19 – 14,903 = -1,71.
Продемонстрируем работу модели (14) для прогнозирования значений временного ряда – доходности долгосрочных облигаций корпораций США на 1992 г. и 1993 г. по данным за девять лет (с 1984 по 1992 г. включительно).
Элементы ковариационной матрицы KYY и вектора ![]() вычислим при помощи модели автоковариационной функции вида (19) с параметрами = 0,7133, = 1,5261 (см. табл. 3):
вычислим при помощи модели автоковариационной функции вида (19) с параметрами = 0,7133, = 1,5261 (см. табл. 3):
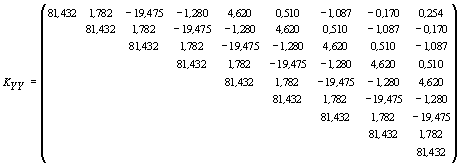
Умножая вектор ![]() :
:
![]()
на вектор ![]() , получим прогноз доходности долгосрочных облигаций корпораций США на 1992 г. В данном случае результат прогноза в точности совпадает с заданным значением, и этот факт был отмечен выше (см. (16)):
, получим прогноз доходности долгосрочных облигаций корпораций США на 1992 г. В данном случае результат прогноза в точности совпадает с заданным значением, и этот факт был отмечен выше (см. (16)):
![]() .
.
Умножая вектор ![]() :
:
![]()
на вектор ![]() , получим прогноз доходности долгосрочных облигаций корпораций США на 1993 г. –
, получим прогноз доходности долгосрочных облигаций корпораций США на 1993 г. –![]() , который отличается от истинного значения на величину = 0,
, который отличается от истинного значения на величину = 0,
0 комментариев