Моделирование дискретной случайной величины и исследование ее параметров

ИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ХАРЬКОВСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ РАДИОЭЛЕКТРОНИКИ

Кафедра РЭС (РТС)

КОНТРОЛЬНАЯ РАБОТА По курсу «Методы проектирования и оптимизации РЭA»

 

Вариант №7

Выполнил: ст.гр. РТз – 98 – 1 Чернов В.В. Шифр 8209127

Проверил: Карташов В. И. ____________________

Харьков 2003

Задание 1. Выполнить моделирование на ЭВМ базовой случайной величины (БСВ) Х. Получить выборки реализаций БСВ объемом n = 170, 1700. Для каждого случая найти минимальное и максимальное значения, оценить математическое ожидание и дисперсию. Сравнить полученные числовые характеристики с теоретическими значениями.

Решение

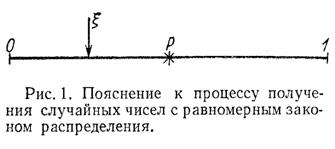
Базовой называют случайную величину, равномерно распределенную на интервале (0,1). Моделирование производится при помощи функции rnd(m) пакета MathCad 2000, возвращающей значение случайной величины, равномерно распределенной в интервале 0xm.

а) для выборки объемом 170 (рис. 1.1): Xmin = 0.0078, Xmax = 0.996.

Первый начальный момент (математическое ожидание) равен среднему арифметическому значений выборки:

М_Х = 0.502 , (1.1)

второй центральный момент (дисперсия):

D =  0.086 , (1.2)

среднеквадратичное отклонение:

s = 0.293 . (1.3)

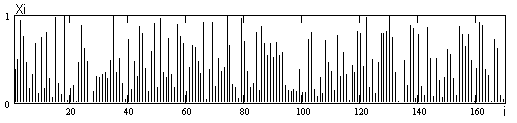
Рисунок 1.1 Выборка объемом 170.

Для выборки объемом 1700 (рис. 1.2): X_min = 0.0037, X_max = 0.998,

М_Х = 0.505 ,  (1.4)

D =  0.085 , (1.5)

 

 s = 0.292 . (1.6)

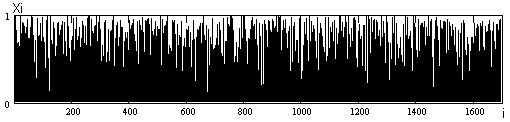
Рисунок 1.2 Выборка объемом 1700.

Теоретически значения математического ожидания и дисперсии БСВ рассчиты-ваются из определения плотности распределения вероятности:

 p_равн(x) =  , (1.7)

математическое ожидание:

M_x = 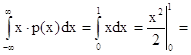0.5 , (1.8)

дисперсия:

D_x =

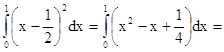
=0.083 , (1.9)

что хорошо совпадает с результатами моделирования (1.1) – (1.5).

Задание 2. Получить выборку реализаций БСВ объемом n = 1700. Построить гистограмму распределений и сравнить ее с плотностью распределения равномерно распределенной случайной величины.

Решение

а) выборка получается аналогично Заданию 1(рис. 2.1):

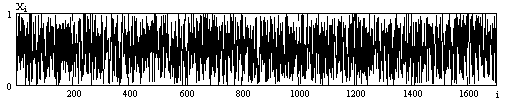
Рисунок 2.1 Выборка объемом 1700

Приняв Xmin = 0, Xmax = 1, разбиваем интервал на q = 10 равных промежутков, каждый из которых равен:

DX = . (2.1)

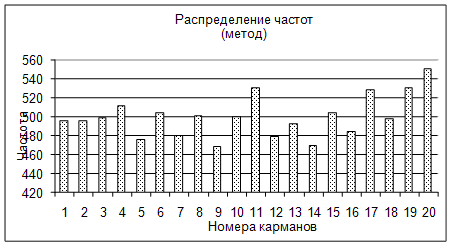
Количества выборок, попадающих в каждый из интервалов, частоты попадания, оценки плотности сведены в табл. 2.1. Гистограмма распределений представлена на рис. 2.2. Как видно, она достаточно хорошо совпадает с равномерным законом распределения (1.7).

Таблица 2.1 Результаты оценки плотности распределения

Номеринтер-вала	1	2	3	4	5	6	7	8	9	10
Диапа-зон значе-ний	0-0.1	0.1-0.2	0.2-0.3	0.3-0.4	0.4-0.5	0.5-0.6	0.6-0.7	0.7-0.8	0.8-0.9	0.9-1
Коли-чество попа-даний	151	174	149	189	190	161	166	182	177	161
Часто-та по-пада-ния Pi	0.089	0.102	0.088	0.111	0.112	0.095	0.098	0.107	0.104	0.095
Оцен-ка плот-ности pi	0.888	1.024	0.876	1.112	1.118	0.947	0.976	1.071	1.041	0.947

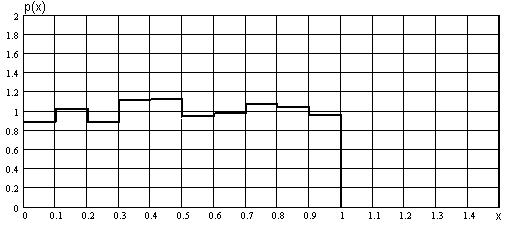
Рисунок 2.2 Гистограмма распределений

Задание 3. Получить выборку БСВ объемом n = 1700, По этой выборке проверить свойства независимости полученной случайной последовательности (вычислить 10 значений коэффициента корреляции).

Решение

а) снова получим выборку значений БСВ объемом n = 1700 (рис. 3.1):

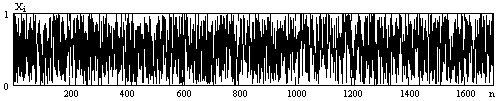
Рисунок 3.1 Выборка объемом 1700

б) значения математического ожидания и дисперсии:

M = 0.512 , (3.1)

D =  0.088 . (3.2)

в) функция корреляции:

R(j) =  ,  (3.3)

значения R(j) для j = 1…10 приведены в табл. 3.1 , значение R(0) = 0.088 совпадает с дисперсией.

Таблица 3.1 Значения функции корреляции:

j	1	2	3	4	5	6	7	8	9	10
R(j)	-9.6·10-4	3.53­·10-3	2.7·10-4	4.24·10-3	-1.73·10-3	6.61·10-4	4.11·10-4	6.74·10-5	3.95·10-4	1.12·10-3

Задание 4. Выполнить моделирование случайной величины, распределенной по закону Релея. Объем выборки n = 17, s² = 27.

Решение

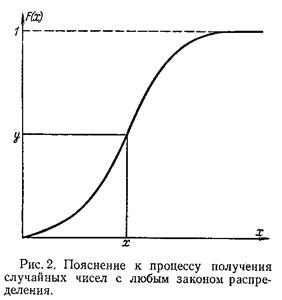
Ддя получения случайной величины с заданным законом распределения из БСВ применим метод обратной функции:

а) для распределения Релея

p(x) = 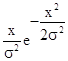(4.1)

случайная величина

x = F(x) = 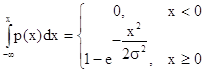(4.2)

равномерно распределена в интервале 0…1, и может быть задана с помощью БСВ. Решив уравнение (4.2) относительно x, получаем случайную величину, распределенную по закону (4.1):

x_i =  ,

x_i = 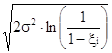 ,  (4.3)

где x_i – значения выборки БСВ

Результат моделирования случайной величины x_i представлен на рис. 4.1:

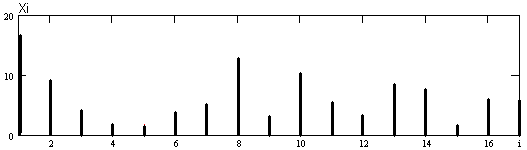
Рисунок 4.1 Выборка случайной величины, распределенной по закону Релея

СПИСОК ЛИТЕРАТУРЫ

1.    Вентцель Е. С. Теория вероятностей. М. Физматгиз, 1962. – 246 с.

2.    Тихонов В. И. и др. Примеры и задачи по статистической радиотехнике. М. – Сов. радио, 1970. – 600 стр.

3.    Трохименко Я.К., Любич Ф.Д. Радиотехнические расчеты на ПК: Справочник. М. – Радио и связь, 1988. – 304 с.