Формирование эконом-математической модели

7602

знака

таблиц

изображений

Формирование экономико-математической модели.

Постановка задачи.

Пусть имеется пять предприятий-изготовителей и одиннадцать потребителей одинаковой продукции. Известны производственные мощности изготовителей и потребности потребителей. Суммарные мощности предприятий больше потребности потребителей.

Производственные мощности изготовителя составляют Ai. Потребность потребителя продукции равна Bj.

На выпуск единицы продукции изготовитель i расходует Ri затрат.

Известны затраты на доставку единицы продукции из пункта i в пункт j – Cij.

Издержки транспорта значительны и должны быть включены в целевую функцию.

Требуется составить такой план производства и поставок, чтобы суммарные расходы на производство и транспортировку были минимальны.

Математическая формулировка задачи.

Удовлетворение всех потребностей:

Xij = Bj

Неотрицательность грузовых потоков:

Xij >= 0

Соблюдение ограничений мощности:

Xij <= Ai

Целевая функция:

(Ri + Cij)*Xij -> min

От обычной транспортной задачи поставленная задача отличается тем, что показатель оптимальности складывается из двух составляющих. Однако, общие затраты на производство и транспортировку определяются простым суммированием.

Таким образом, поставленная задача является открытой транспортной задачей.

Исходные данные

Предприятие	А1		А2		А3		А4		А5
Производственные мощности	135		160		140		175		165
Затраты на ед. продукции в рублях	119		93		81		70		62
Потребители	В1	В2	В3	В4	В5	В6	В7	В8	В9	В10
Спрос потребителей	30	45	60	50	45	65	79	87	44	30

Матрица транспортных затрат, руб.

(получена на основе данных по сети)

Потребители		B1	B2	B3	B4	B5	B6	B7	B8	B9	B10
Отправители	Номера вершин	3	12	24	35	19	30	16	9	31	5
A1	2	41	34	45	64	41	46	31	38	41	18
A2	33	47	22	12	21	13	7	12	36	2	36
A3	26	35	14	7	33	1	5	16	24	10	24
A4	21	40	40	38	39	31	37	42	29	42	51
A5	13	21	16	19	47	13	19	18	10	24	19

Суммированием затрат на производство и транспортных затрат в каждой клетке матрицы получаем расчетную матрицу.

Расчетная матрица стоимостных затрат.

Потребители		B1	B2	B3	B4	B5	B6	B7	B8	B9	B10
Отправи тели	Ресурсы
A1	135	160	153	164	183	160	165	150	157	160	137
A2	160	140	115	105	114	106	100	105	129	95	129
A3	140	116	95	88	114	82	86	97	105	91	105
A4	175	110	110	108	109	101	106	112	99	112	121
A5	165	83	78	81	109	75	81	80	72	86	81

Так как транспортная задача открытая, то мощности превышают потребности. Часть поставщиков в оптимальном плане остается недозагруженной. Для решения задачи в матричной форме вводится фиктивный потребитель – дополнительный столбец с потребностью, равной избытку ресурсов над реальными потребностями.

Решение транспортной задачи.

Исходные данные.

Потребители		B1	B2	B3	B4	B5	B6	B7	B8	B9	В10	В11
Отправи тели	Ресурсы	30	45	60	50	45	65	79	87	44	30	240
A1	135	160	153	164	183	160	165	150	157	160	137	0
A2	160	140	115	105	114	106	100	105	129	95	129	0
A3	140	116	95	88	114	82	86	97	105	91	105	0
A4	175	110	110	108	109	101	106	112	99	112	121	0
A5	165	83	78	81	109	75	81	80	72	86	81	0

Итого 775

Решение

Потребители		B1	B2	B3	B4	B5	B6	B7	B8	B9	B10	B11
Отправи тели	Ресурсы	30	45	60	50	45	65	79	87	44	30	240
A1	135	160	153	164	183	160	165	150	157	160	137	0
												135
A2	160	140	115	105	114	106	100	105	129	95	129	0
								49		44		67
A3	140	116	95	88	114	82	86	97	105	91	105	0
						45	65	30
A4	175	110	110	108	109	101	106	112	99	112	121	0
					20				87		30	38
A5	165	83	78	81	109	75	81	80	72	86	81	0
		30	45	60	30

Итого 775

Для подтверждения правильности решения оптимальный план, полученный в данной таблице проверяется методом потенциалов на соблюдение условий оптимальности .

Условие оптимальности выглядит следующим образом:

Vij – Uij <= Cij

Vij – Uij = Cij , если Xij > 0

Для всех клеток матрицы разность потенциалов столбца и строки меньше или равна показателю оптимальности, для занятых клеток точно равна его значению.

Первый потенциал может быть присвоен любой строке или столбцу. В данном случае первый потенциал присвоен базисной клетке, где затраты на транспортировку максимальны (А4 – В10).

Проверка решения методом потенциалов.

Потребители		B1	B2	B3	B4	B5	B6	B7	B8	B9	B10	B11
Отправител	Ресурсы	30	45	60	50	45	65	79	87	44	30	240
A1	135	160	153	164	183	160	165	150	157	160	137	0	150
												135
A2	160	140	115	105	114	106	100	105	129	95	129	0	150
								49		44		67
A3	140	116	95	88	114	82	86	97	105	91	105	0	158
						45	65	30
A4	175	110	110	108	109	101	106	112	99	112	121	0	150
					20				87		30	38
A5	165	83	78	81	109	75	81	80	72	86	81	0	150
		30	45	60	30
		233	228	231	259	240	244	255	249	245	271	150

Потребители		B1	B2	B3	B4	B5	B6	B7	B8	B9	B10	B11
Отправител	Ресурсы	30	45	60	50	45	65	79	87	44	30	240
A1	135	50	48	62	74	64	65	45	51	50	35	0
												135
A2	160	30	10	3	5	10	0	0	30	0	27	0
							30	79		44		7
A3	140	20	4	0	19	0	0	6	20	10	17	20
				60		45	35
A4	175	0	5	6	0	5	6	7	0	17	19	0
					50				27			98
A5	165	0	0	0	27	0	2	2	0	18	0	27
		30	45						60		30

Далее следует сравнить Целевую функцию в решении задачи (F1) и целевую функцию, полученную при решении потенциалов (F2), если F1 > F2, то план оптимален.

Потребители		B1	B2	B3	B4	B5	B6	B7	B8	B9	B10	B11
Отправите	Ресурсы	30	45	60	50	45	65	79	87	44	30	240
A1	135	160	153	164	183	160	165	150	157	160	137	0
												135
A2	160	140	115	105	114	106	100	105	129	95	129	0
								49		44		67
A3	140	116	95	88	114	82	86	97	105	91	105	0
						45	65	30
A4	175	110	110	108	109	101	106	112	99	112	121	0
					20				87		30	38
A5	165	83	78	81	109	75	81	80	72	86	81	0
		30	45	60	30
Цел. Ф-ия (F1)		2490	3510	4860	5450	3690	5590	8055	8613	4180	3630	0
Цел. Ф-ия (F1)		50068


Потребители		B1	B2	B3	B4	B5	B6	B7	B8	B9	B10	B11
Отправител	Ресурсы	30	45	60	50	45	65	79	87	44	30	240
A1	135	160	153	164	183	160	165	150	157	160	137	0
												135
A2	160	140	115	105	114	106	100	105	129	95	129	0
							30	79		44		7
A3	140	116	95	88	114	82	86	97	105	91	105	0
				60		45	35
A4	175	110	110	108	109	101	106	112	99	112	121	0
					50				27			98
A5	165	83	78	81	109	75	81	80	72	86	81	0
		30	45						60		30
Цел. Ф-ия (F2)		2490	3510	5280	5450	3690	6010	8295	6993	4180	2430	0
Цел. Ф-ия (F2)		48328

Т.к. 50068 > 48328 , то план оптимален, т.е. условие оптимальности соблюдается во всех клетках матрицы, следовательно задача решена правильно.

Вывод.

Разработанный оптимальный план обеспечивает минимальные затраты на производство и транспортировку продукции из пяти пунктов производства в десять пунктов потребления.

На основе решения транспортной задачи определены поставки каждого пункта производства в пункты потребления, производственные программы по заводам изготовителям и резервы производственных мощностей.

Резерв производственной мощности на заводе А1 составляет 135 единиц (поставки фиктивному потребителю), на заводе А2 – 7 единиц, на заводе А4 – 98 единиц, остальные предприятия резервов не имеют.

Минимальные затраты на транспортировку и производство составили 48328 рублей. Затраты на производство продукции в составе суммарных затрат определяются умножением затрат на производство единицы продукции на производственную программу и составят:

119*0+93*153+81*140+70*77+62*165= 14229+11340+5390+10230=41189 рублей или 85,2%.

Затраты на транспортировку составляют 7139 рублей или 14,8%. Такую долю транспортных затрат для готовой продукции следует считать довольно высокой, хотя по отдельным видам дешевых массовых грузов эта доля может быть значительно выше.

Раздел: Экономико-математическое моделирование
Количество знаков с пробелами: 7602
Количество таблиц: 8
Количество изображений: 0

Скачать

... на них, оценки технико-экономических показателей и, в завершении, построения экономико-математической модели предприятия. В экономико-математической модели в целевую функцию должен вводиться тот или иной фактор неопределенности. В дальнейшем будет приведена разработка методика учета факторов неопределенности, показаны математические модели снятия неопределенности. Крайне важным является оценка ...

Скачать

... ситуации является определяющим фактором [7]. В зависимости от того, какой метод анализа модели выбран, факторныe разложения могут различаться. Глава 2. Применение детерминированных экономико-математических моделей и методов факторного анализа на примере РУП «ГЗЛиН». 2.1 Характеристика РУП «ГЗЛиН» 9 октября 1979 - издан приказ М 272 Министерства машиностроения для животноводства и ...

Скачать

... производства, чем (6.3.4), представляется равенство где - отнесенный к моменту t временной лаг, (). Обозначим и составим матрицы с помощью которых систему (6.3.1)-(6.3.5) перепишем в виде В математической экономике магистралью называется траектория экономического роста, на которой пропорции производственных показателей (такие как темп роста производства, темп снижения цен) неизменны ...

Скачать

... ; - развитие теорий мотивации; - история возникновения системного анализа. Отметим, что "Оригинальная методика анализа альтернативных подходов к формированию структуры организации" стала венцом взаимодействия направлений "Теории управления" использующих как чисто количественные методы, так и учитывающих человеческий фактор. Глава 2. Три источника (три составных части) "Оригинальной ...

Главная Новости Рефераты Статьи Вузы

О проекте Соглашение

Наверх

Войти на сайт

Навигация

Похожие работы

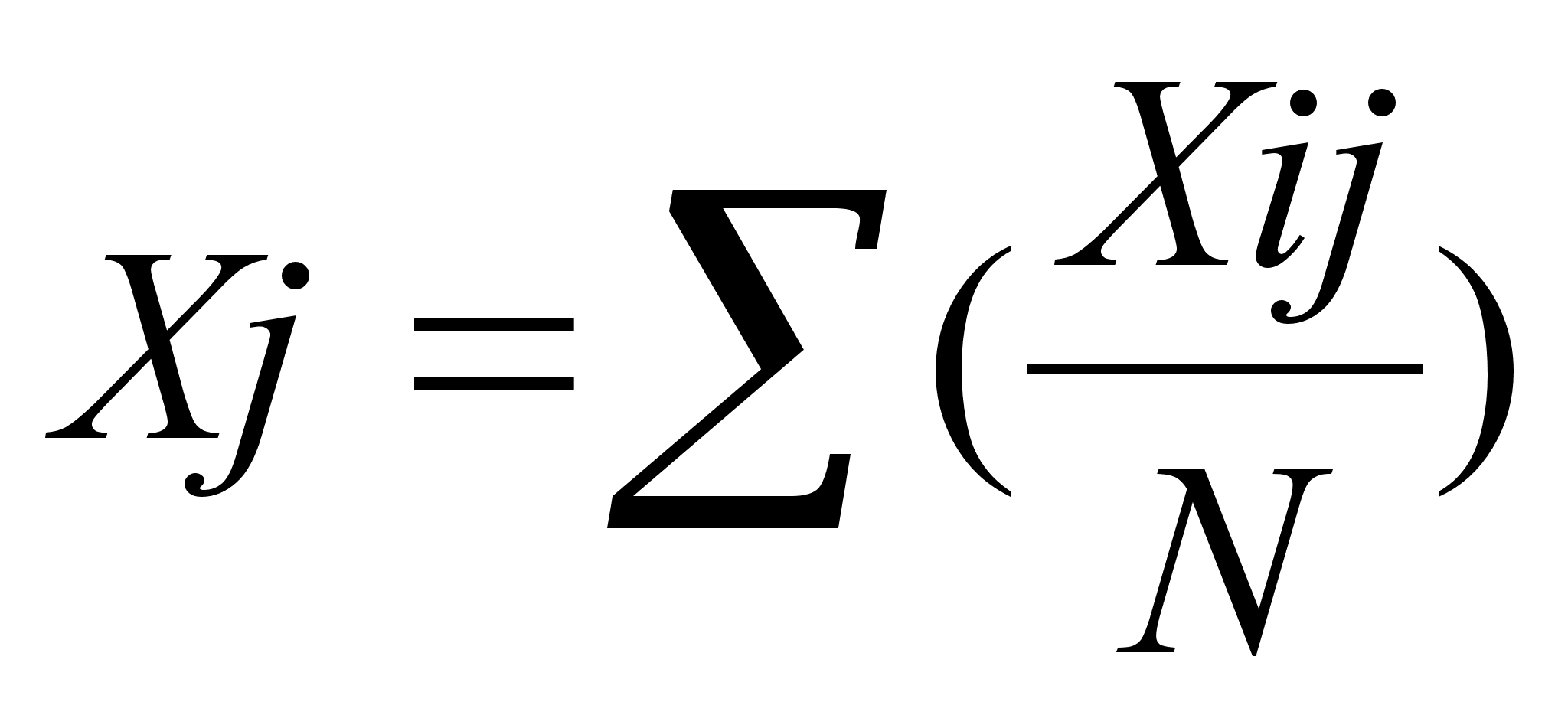
0 комментариев

Разделы

Инфо

Следите за новостями