Аркадий Гуртовцев, к.т.н., ведущий научный сотрудник РУП «БелТЭИ», г. Минск, Республика Беларусь
Каждый электронный электросчетчик имеет свой класс точности, который производители указывают в паспортных данных. Но какая реальность стоит за этим?
Точность средства измерения (СИ) отражает возможную близость его погрешности к нулю при определенных условиях измерения. Уровень точности задается обобщенной характеристикой типа СИ – классом точности, определяющим пределы допускаемых основной (погрешности СИ в нормальных условиях) и дополнительных погрешностей (составляющих погрешности СИ, возникающих дополнительно к основной, вследствие отклонения какихлибо из влияющих величин от нормальных их значений), а также другие характеристики, влияющие на точность [1].
На практике часто забывают, что номинальный класс точности конкретного СИ, указываемый обычно в виде целого или дробного десятичного числа в его паспорте и на приборе, привязан не к любым, а именно к нормальным условиям (НУ) измерений, характеризуемым совокупностью значений влияющих величин, при которых изменением результата измерений пренебрегают вследствие малости. Реально же СИ используют в рабочих (когда значения влияющих величин находятся в рабочих областях, в пределах которых нормируют дополнительные погрешности) или даже предельных (экстремальных значениях измеряемых и влияющих величин, которые СИ может выдержать без разрушений и ухудшений метрологических характеристик) условиях измерений. При эксплуатации в условиях, отличающихся от НУ, погрешность конкретного СИ необходимо оценивать не по номинальной величине его класса точности, а по сумме основной и возможных дополнительных погрешностей.
Представляет интерес проведение общего анализа суммарных предельных и реальных основных и дополнительных погрешностей СИ, используемых в коммерческом учете электрической энергии, – современных электронных счетчиков электроэнергии (далее – счетчики). В качестве базы возьмем, с одной стороны, новые стандарты РФ [2–4], а с другой стороны, данные испытаний электронных многотарифных счетчиков различных изготовителей из России, Беларуси и Украины, проведенных в 2004–2006 гг. в аккредитованном Госстандартом испытательном центре Белорусской энергосистемы. Было испытано в общей сложности 56 типов счетчиков различных классов точности в количестве 276 образцов от 14 изготовителей. Эти испытания проводились по утвержденной отраслевой программе и ГОСТ [5, 6], на смену которым пришли вышеупомянутые новые стандарты. Отдельные результаты испытаний 2004 года рассмотрены в [7], но в аспекте, отличном от подхода в настоящей работе.
Прежде чем перейти к анализу погрешностей счетчиков, уточним некоторые метрологические понятия и требования стандартов к основным и дополнительным погрешностям счетчиков.
Метрологические требованияСогласно [2], класс точности счетчика определяется как число, равное пределу основной допускаемой погрешности, выраженной в форме относительной погрешности оп в процентах, для определенных значений тока нагрузки Iн в диапазоне от 0,1 Iб (Iб – базовый ток, т.е. значение тока, являющееся исходным для установления требований к счетчику с непосредственным включением) до Iмакс (Iмакс – наибольшее значение тока, при котором счетчик удовлетворяет установленным требованиям точности) или от 0,05 Iном (Iном – значение тока, являющееся исходным для установления требований к счетчику, работающему от трансформатора) до Iмакс – установленном диапазоне измерений – при коэффициенте мощности, равном 1 (в том числе в случае многофазных счетчиков – при симметричных нагрузках), при испытании счетчика в нормальных условиях (с учетом допускаемых отклонений от номинальных значений), установленных в стандартах, определяющих частные требования.
Частные требования к электронным счетчикам активной энергии классов точности 1 и 2 установлены в [3], а классов точности 0,2S и 0,5S – в [4]. Литера S означает, что класс точности счетчика нормируется, начиная с нижней границы не 5% Iном (как для счетчиков без литеры, например, классов 0,2 и 0,5), а 1% Iном (ниже этой границы погрешность не нормируется, хотя счетчик и производит измерения электроэнергии, мощность которой превышает чувствительность счетчика).
Верхняя граница установленного диапазона измерения определяется величиной Iмакс, которая для счетчиков трансформаторного включения должна выбираться изготовителем, согласно [2], из множества значений (1,2; 1,5; 2,0 или 6,0) Iном. В свою очередь Iном для таких счетчиков должен иметь значение 1; 2 или 5 А (для счетчиков непосредственного включения выбор стандартных значений базовых токов производится из более широкого диапазона значений 5…100 А и, в частности, для однофазного счетчика должен быть не менее 30 А).
Стандартные НУ проверки точности счетчиков классов 0,2S, 0,5S, 1 и 2 приведены ниже, в табл. 1 [3, 4].
Дополнительно к указанным НУ для многофазных счетчиков напряжения и токи должны быть практически симметричными (отклонения от средних значений не должны превышать 1–2%).
Границы, или пределы Гоп основной погрешности счетчика оп, вызываемой изменениями тока Iн и видом нагрузки (активной при КМ = 1, реактивной – емкостной Е или индуктивной И с соответствующими значениями КМ) при НУ, не должны превышать пределов для соответствующего класса точности одно и многофазных счетчиков с симметричными нагрузками [3, 4] (табл. 2).
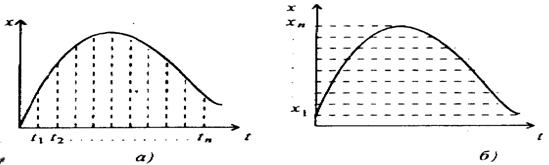
Из табл. 2 следует, что даже в НУ, но при изменении тока и вида нагрузки, предел Гоп основной допускаемой погрешности оп счетчика увеличивается относительно номинала класса точности в 2–2,5 раза. В частности, для счетчиков трансформаторного включения классов 0,2S и 0,5S это имеет место, вопервых, в диапазоне тока до 5% Iном при активной нагрузке, и, вовторых, в диапазоне тока до 10% Iном при реактивной нагрузке (в диапазоне до Iмакс предел погрешности увеличивается в 1,5 раза). На рис. 1 приведен график пределов основной погрешности счетчика класса 0,2S, соответствующий табл. 2.
Пределы Гдп дополнительной погрешности дп, вызываемой влияющими величинами (по отношению к НУ), для счетчиков классов точности 0,2S; 0,5S и 1; 2 приведены соответственно в табл. 3 и 4 [3, 4].
Рис. 1. График пределов основной погрешности счетчика класса 0,2S

Iч – ток чувствительности счетчика, при котором погрешность не определена, но велика.
Таблица 1. Нормальные условия проверки счетчика на точность
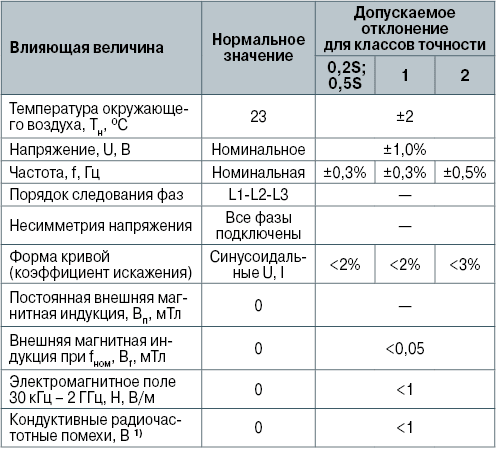
1) Под кондуктивной (от лат. сonductor – проводник) электромагнитной помехой понимается, согласно [8], электромагнитная помеха, распространяющаяся не из окружающего воздушного пространства, а по элементам электрической сети, т.е. по проводам.
Таблица 2. Пределы допускаемой основной погрешности счетчиков при НУ
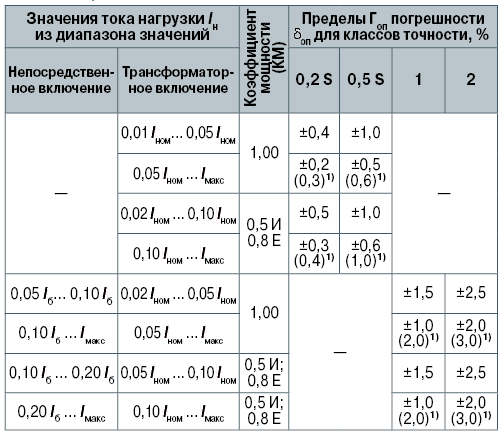
1) Погрешности для многофазных счетчиков с однофазной нагрузкой, но при сохранении симметрии многофазных напряжений.
АНАЛИЗ СУММАРНЫХ ПРЕДЕЛЬНЫХ ПОГРЕШНОСТЕЙ СЧЕТЧИКОВ
Если бы каждый счетчик эксплуатировался в НУ (см. табл. 1), то он имел бы только основную погрешность оп, которая не превышала бы пределов, указанных в табл. 2:
| оп < Гоп (Iн, КМ). | (1) |
Значения предела Гоп (Iн, КМ) зависят от режима работы нагрузки (величины тока нагрузки Iн и КМ) и регламентированы в конкретном ее диапазоне. Вне этого диапазона (например, при КМ, отличном от 1; 0,5 И или 0,8 Е) предел не определен и о его значениях нечего сказать.
Зададимся вопросом, к каким видам погрешностей относится основная погрешность счетчика, является она систематической или случайной? Согласно [1], систематической погрешностью измерения является составляющая результата измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины (различают постоянные, прогрессивные, периодические и сложноизменяющиеся систематические погрешности). Ее противоположностью является случайная погрешность – составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных с одинаковой тщательностью, одной и той же физической величины. Отметим еще два вида погрешностей: инструментальную составляющую погрешности измерения, обусловленную погрешностью применяемого средства измерения, и погрешность метода – составляющую систематической погрешности измерений, обусловленную несовершенством принятого метода измерения.
Очевидно, что основная погрешность электронного счетчика является систематической погрешностью, в основе которой лежат неустранимые погрешности метода измерения и инструментальной погрешности самого счетчика (погрешности изготовления и настройки его технологических элементов). Но при этом в паспорте от любого изготовителя на счетчик конкретного типа и класса точности указываются, в соответствии с требованиями стандартов [2–4], не конкретные систематические погрешности счетчика, а их пределы, причем со знаками плюсминус, что должно свидетельствовать о равновероятности их обоюдного появления в процессе измерений (см. табл. 2).
Такое задание предельной погрешности счетчика подразумевает возможность отклонения измеренной величины от ее действительного (истинного) значения как в сторону его переоценки (при положительной погрешности), так и, наоборот, в сторону недооценки (при отрицательной погрешности).
Априорно о знаках реальной основной погрешности и ее реальных пределах субъекту учета, как правило, ничего не известно. Имели место случаи, когда некоторые покупатели крупных партий счетчиков, пользуясь неопределенностью задания пределов допускаемых основных погрешностей счетчиков, заключали с изготовителем счетчиков недобросовестное соглашение по коррекции погрешностей партии счетчиков в рамках их класса точности в сторону одного знака (в процессе регулировки и настройки счетчиков это несложно выполнить). Если покупатель представлял интересы потребителя электроэнергии, то он просил изготовителя выставить погрешность счетчиков в минус, а если продавца электроэнергии, то, наоборот, в плюс (часто, как будет показано ниже, такой крен знака погрешности возникает в процессе заводского производства счетчиков непроизвольно). Таким образом, систематический характер основной погрешности счетчика получал в указанных сделках свое потребительское воплощение.
В общем случае, когда в учете электроэнергии используются счетчики разных типов и классов точности от различных изготовителей, у субъектов учета отсутствуют какиелибо данные о погрешностях счетчиков, кроме их пределов, взятых с равновероятными знаками плюсминус. Только эти данные и могут быть положены, как правило, в основу оценки погрешностей измерений электроэнергии. Поскольку пределы погрешностей связаны с режимами работы нагрузки, то в тех случаях, когда эти режимы известны и стабильны во времени, для оценки результатов измерений можно выбрать соответствующие значения пределов из табл. 2.
Таблица 3. Пределы допускаемой дополнительной погрешности для счетчиков классов 0,2S и 0,5S
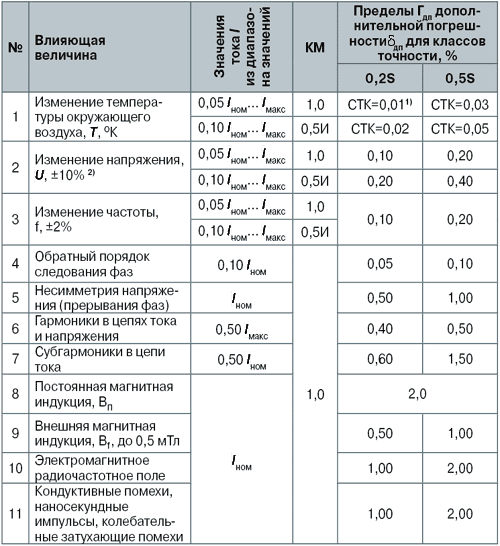
1) СТК – средний температурный коэффициент, % / 1 ОС;
2) при изменении U вне указанных пределов погрешность может увеличиться в 3 раза.
Таблица 4. Пределы допускаемой дополнительной погрешности для счетчиков классов 1 и 2
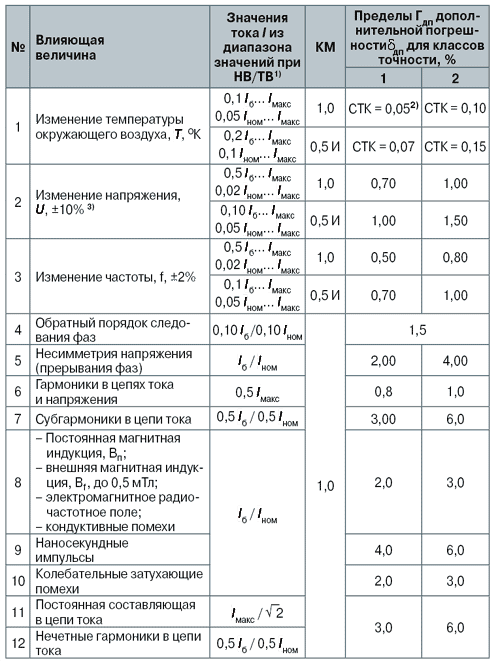
1) НВ/ТВ соответственно непосредственное и трансформаторное включение счетчика;
2) СТК – средний температурный коэффициент, % / 1 OС;
3) при изменении U вне указанных пределов погрешность может увеличиться в 3 раза.
В большинстве же случаев, когда в течение времени значительно меняется как ток нагрузки, так и ее активнореактивный характер (например, за счет включения или отключения потребителем тех или иных электроустановок), для оценки результатов измерений при НУ следует выбирать максимальные пределы из возможных, т.е. проводить расчет на наихудший случай. Для счетчиков классов точности 0,2S, 0,5S, 1 и 2 эти пределы имеют соответственно значения ±0,5, ±1,0, ±2,0 и ±3,0, т.е. в 2,5–1,5 раза превышают номинальный класс точности счетчика. Если в процессе учета электроэнергии имеются какиелибо статистические указания на преобладание в течение расчетного периода тех или иных режимов нагрузки, то эти данные можно учесть, понизив соответствующим образом указанные максимальные пределы основной погрешности.
Одна из основных задач при производстве измерений заключается в обнаружении и исключении систематических погрешностей. Их появление, как при однократном измерении, так и в многократных повторениях одних и тех же измерений, выполняемых с помощью одного и того же метода и средства измерения, обусловлено совокупностью факторов, действующих устойчиво и одинаковым образом. Поэтому, например, при измерении фиксированного значения физической величины (принимается по умолчанию, что значение случайной составляющей погрешности существенно меньше значения систематической составляющей) систематическая погрешность будет одинакова при всех повторениях, но при этом поправка на величину погрешности, которую можно было бы использовать для коррекции результата измерения, чаще всего неизвестна. Для счетчика известно только то, что погрешность не превышает конкретного предела. Такие погрешности целесообразно классифицировать, согласно [9], как «систематические погрешности известного происхождения, но неизвестной величины».
Их принципиально нельзя исключить из процесса измерения, а можно только оценить через предельные неравенства вида (1), а также уменьшить за счет использования СИ более высокого класса точности и обеспечения фиксированных условий измерений. Скрытие реальных систематических основных погрешностей счетчика под маской равновероятных пределов (они равновероятны, так как нет оснований в конкретных измерениях, следуя паспортным данным СИ, предпочесть предел со знаком плюс пределу со знаком минус) позволяет рассматривать эти погрешности как псевдослучайные. Их принципиальное отличие от случайных погрешностей заключается в том, что к ним неприменимы, вообще говоря, статистические методы повышения точности, которые действуют для действительно случайных величин и погрешностей (для последних, многократно повторяя измерения и применяя соответствующую статистическую обработку, можно свести погрешность в пределе к нулю).
В следующем номере журнала мы продолжим разговор о погрешностях электронных электросчетчиков и приведем статистические результаты испытаний шести конкретных типов счетчиков 5 производителей.
Список литературы1. РМГ 2999. Метрология. Основные термины и определения. – Минск, 2002.
2. ГОСТ Р 523202005. Аппаратура для измерения электрической энергии переменного тока. Общие требования. Испытания и условия испытаний. Ч.11: Счетчики электрической энергии. – М.: Стандартинформ, 2005.
3. ГОСТ Р 523222005. Аппаратура для измерения электрической энергии переменного тока. Частные требования. Ч. 21: Статические счетчики активной энергии классов точности 1 и 2. – М.: Стандартинформ, 2005.
4. ГОСТ Р 523232005. Аппаратура для измерения электрической энергии переменного тока. Частные требования. Ч. 22: Статические счетчики активной энергии классов точности 0,2S и 0,5S. – М.: Стандартинформ, 2005.
5. ГОСТ 3020794. Статические счетчики ваттчасов активной энергии переменного тока (классы точности 1 и 2). – Минск: Белстандарт,1998.
6. ГОСТ 3020694. Статические счетчики ваттчасов активной энергии переменного тока (классы точности 0,2S и 0,5S). – Минск: Белстандарт, 1997.
7. Гуртовцев А.Л, Бордаев В.В, Чижонок В.И. Электронные электросчетчики. Доверять или проверять? // Новости ЭлектроТехники. – 2005. – № 1(31), 2(32).
8. ГОСТ 1310997. Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения. – Минск, 1999.
9. Зайдель А.Н. Погрешности измерений физических величин. – Л.:Наука, 1
Похожие работы
... 674 тыс. руб в год. В заключение можно сделать следующие выводы: уменьшение нагрузок в ряде узлов энергосистемы, а также снижение потребления электроэнергии промышленностью привели к возникновению отрицательной погрешности у трансформаторов тока и соответственно к коммерческому недоучету потребленной энергии; для устранения недоучета потребления электроэнергии необходимо вводить корректирующие ...
... энергосистемы. Таким образом, сложившаяся ситуация способствует хищениям электроэнергии, так как не позволяется эффективно с ними бороться. В настоящее время энергосбыт ведет активную работу по обнаружению и борьбе с хищениями электроэнергии. Контролеры энергосбыта производят осмотр приборов учета каждого бытового потребителя не реже одного раза в год. Планируется увеличить количество осмотров до ...
... измерения энергии должна находится в пределах ±(0,1-2,5)%. 4.4 Зависимость погрешности дозирования от состава технических средств комплексов дозирования Поскольку в электротехнические комплексы дозирования помимо рассмотренных выше устройств цифрового дозирования количества электричества и электрической энергии входят также устройства коммутации и датчики тока и напряжения, то необходимо ...
... или программной обработки результатов измерения (например, построение графиков зависимости емкости или индуктивности от температуры в реальном масштабе времени и т.п.) возможность программирования прибора для сортировки и отбраковки компонентов на производстве; возможность подключения механического манипулятора. Принцип измерения всех измерителей импеданса (иммитанса) основан на анализе ...





0 комментариев