Контрольная работа студента Заочного факультета ССиСК 5 курса 1гр. шифр 963249 Ходус Александра Юрьевича.
Поволжская Государственная Академия телекоммуникаций и информатики
Ставропольский филиал
Ставрополь 1999г.
Задача № 1.Межузловая ветвь вторичной сети, имеющая один канал, принимает простейший поток сообщений с интенсивностью l=0,04 сообщений в секунду. Время передачи сообщений по каналу связи распределено по экспоненциальному закону. Среднее время передачи одного сообщения составляет t = 14 секунд. Сообщения, поступающие в моменты времени, когда обслуживающий канал занят передачей ранее поступившего сообщения, получают отказ передачи.
Определить следующие показатели эффективности ветви связи вторичной сети связи при условии её работы в установившемся режиме:
Pотк – вероятность отказа приёма сообщения для передачи для передачи по межузловой ветви;
Pзан – вероятность занятости канала связи (коэфф. относительной загрузки канала);
Q – относительная пропускная способность межузловой ветви;
A – абсолютная пропускная способность межузловой ветви.
Решение:
Найдём m и r:
Найдём в начале вероятность нулевого состояния анализируемой СМО, при котором канал связи свободен и поступающее сообщение будет принято для передачи по каналу связи:
Вероятность отказа приёма для передачи по каналу связи межузловой ветви:
Для одноканальной СМО с отказами вероятность свободного состояния P0 численно равна Q – относительной пропускной способности СМО.
Абсолютная пропускная способность межузловой ветви: Задача № 2.
Межузловая ветвь вторичной сети связи, имеющая один канал и неограниченный по объёму накопитель очереди ожидающих сообщений, принимает простейший поток сообщений с интенсивностью l = 0,04 сообщений в секунду. Время передачи сообщений распределено по экспоненциальному закону. Среднее время передачи одного сообщения составляет t = 14 секунд. Сообщения, поступающие в моменты времени, когда обслуживающий канал занят передачей ранее поступившего сообщения, принимаются в очередь и не покидают её до момента до начала передачи по каналу связи.
Определить следующие показатели эффективности ветви связи вторичной сети:
Lоч – среднее число сообщений в очереди к ветви связи вторичной сети;
Lсист – среднее суммарное число сообщений в очереди и передающихся по ветви связи вторичной ветви;
Точ – среднее время пребывания сообщения в очереди до начала передачи;
Тсист – среднее суммарное время пребывания сообщения в системе, складывающееся из среднего времени ожидания в очереди и среднего времени передачи;
Рзан – вероятность занятости канала связи (коэфф. относительной загрузки канала);
Q – относительную пропускную способность межузловой ветви;
А - абсолютную пропускную способность межузловой ветви;
Решение:
Найдём в начале вероятность нулевого состояния анализируемой СМО, при котором канал связи свободен и
в накопителе очереди нет ни одного сообщения:
Вероятность отказа приёма сообщения для передаче по каналу связи межузловой ветви в СМО с бесконечно большим накопителем очереди будет равна нулю при условии r < 1.
Lоч – среднее число сообщений в очереди к ветви связи вторичной сети:
Lсист – среднее суммарное число сообщений в очереди и передающихся по ветви связи вторичной ветви:
Точ – среднее время пребывания сообщения в очереди до начала передачи:
Тсист – среднее суммарное время пребывания сообщения в системе, складывающееся из среднего времени ожидания в очереди и среднего времени передачи:
Относительная пропускная способность Q межузловой ветви c бесконечным накопителем очереди численно равна доле сообщений в поступающем потоке, принимаемых для передачи (не получаемых отказа). При отсутствии перегрузки канала связи (r < 1) она будет равна единице.
Абсолютная пропускная способность межузловой ветви с бесконечным накопителем очереди при условии отсутствия перегрузке канала связи (r < 1) будет равна интенсивности потока l поступающих для передачи сообщений.
Задача № 3.Группа из n = 35 шнуровых комплектов, соединяющих выходы коммутационного блока абонентских линий и выходы коммутационного блока соединительных линий аналоговой АТС, обслуживает группу, состоящую из k = 140 абонентов телефонной станции. Каждым абонентом этой группы за один час подается r = 2 заявок на установление соединения с другим абонентом телефонной сети. Средняя продолжительность сеанса связи равна t = 11 минут. Определить среднее число Z занятых шнуровых комплектов, вероятность Ротк – получение вызывающим абонентам отказа в предоставлении свободного шнурового комплекта, Q – относительную долю обслуженных вызовов от общего числа поступивших вызовов, А – абсолютную пропускную способность группы шнуровых комплектов.
Решение:
Для решения поставленной задачи необходимо вначале определить общую интенсивность l потока заявок, поступающих от 140 абонентов АТС на обслуживание их группой из 35 шнуровых комплектов:
Найдём теперь m - интенсивность обслуживания заявок, равную числу заявок, которые могут быть обслужены одним шнуровым комплектом АТС за один час работы:
Далее найдём r - среднюю относительную нагрузку от 140 абонентов АТС на группу из 35 шнуровых комплектов:
Пользуясь формулой Эрланга найдем вероятность получения абонентом отказа в обслуживания вызовов из-за занятости в момент поступления всех шнуровых комплектов:
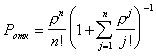 | 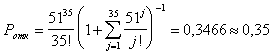 |
Найдём Q – относительная пропускная способность СМО, численно равной средней доле обслуженных заявок от общего числа пришедших заявок:
А – абсолютная пропускная способность, измеряемая средним числом заявок обслуживаемых системой за час, будет равна:
Z – среднее число занятых шнуровых комплектов: Задача № 4.
Межузловая ветвь вторичной сети связи, имеющая один канал и накопитель очереди для m = 4 ожидающих сообщений, принимает простейший поток сообщений с интенсивностью l = 8 сообщений в секунду. Время передачи сообщений распределено по экспоненциальному закону. Среднее время передачи одного сообщения составляет t = 0,1 секунду. Сообщения, поступающие в моменты времени, когда обслуживающий канал занят передачей ранее поступившего сообщения и в накопителе отсутствует свободное мсто, получают очереди отказ.
Определить следующие показатели эффективности ветви связи вторичной сети:
Ротк – вероятность отказа приёма сообщения для передачи по каналу связи межузловой ветви;
Lоч – среднее число сообщений в очереди к ветви связи вторичной сети очереди;
Lсист – среднее суммарное число сообщений в очереди и передающихся по ветви связи вторичной сети;
Точ – среднее время пребывания сообщения в очереди до начала передачи;
Тсист – среднее суммарное время пребывания сообщения в системе, складывающееся из среднего времени ожидания в очереди и среднего времени передачи;
Рзан – вероятность занятости канала связи (коэфф. относительной загрузки канала);
Q – относительную пропускную способность межузловой ветви;
А - абсолютную пропускную способность межузловой ветви;
Решение:
Найдём в начале вероятность нулевого состояния анализируемой СМО, при котором канал связи свободен и в накопителе очереди нет ни одного сообщения:
Вероятность отказа приёма сообщения для передачи его по каналу связи межузловой ветви:
Полученное значение вероятности отказа приёма сообщения для передачи по каналу связи при наличии даже небольшого накопителя очереди (m=4) существенно больше, чем было получено выше в первом примере для одноканальной системы связи с интенсивностью l = 0,04 и
t = 14 секунд, не имеющих накопителя для ожидающих передачи сообщений. Там вероятность отказа передачи сообщения была равна 3,63.
Относительная пропускная способность СМО будет равна вероятности приёма очередной заявки в систему:
Абсолютная пропускная способность СМО будет равна:
Среднее число сообщений в накопителе очереди будет равно:
Среднее суммарное число сообщений, находящихся в очереди и передающихся по ветви связи будет равно:
Задача № 5.
Межузловая ветвь вторичной сети связи имеет n = 4 каналов. Поток сообщений, поступающих для передачи по каналам ветви связи, имеет интенсивность l = 8 сообщений в секунду. Среднее время t = 0,1 передачи одного сообщения равно t/n = 0,025 секунд. В накопители очереди ожидающих передачи сообщений может находиться до m = 4 сообщений. Сообщение прибывшее в момент, когда все m мест в очереди заняты, получает отказ передачи по ветви связи. Найти характеристики СМО:
Ротк – вероятность отказа передачи сообщений;
Q – относительную пропускную способность межузловой ветви;
А – абсолютную пропускную способность межузловой ветви;
Z – среднее число занятых каналов;
Lоч – среднее число сообщений в очереди;
Тож – среднее время ожидания;
Тсист – среднее суммарное время пребывания сообщения в очереди и его передачи по ветви связи. ![]()
Решение:
![]()
![]()
![]()
Найдём вначале вероятность нулевого состояния СМО:
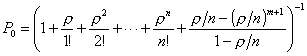
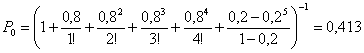
Вероятность отказа передачи по ветви связи будет равна:
![]()
![]()
![]()
![]()
Относительная пропускная способность:
![]()
![]()
Абсолютная пропускная способность:
![]() сообщений/с.
сообщений/с.
Среднее число занятых каналов связи:
Среднее число сообщений в накопителе очереди определим по формуле:
![]()
![]() сообщ.
сообщ.
Среднее время ожидания в очереди:
![]()
![]() с.
с.
Среднее суммарное время пребывания сообщения в очереди и его передачи по ветви связи:
![]() с.
с.
Межузловая ветвь вторичной сети связи имеет n = 4 каналов. Поток сообщений, поступающих для передачи по каналам ветви связи, имеет интенсивность l = 8 сообщений в секунду. Среднее время t = 0,1 передачи одного сообщения каждым каналом связи равно t/n = 0,025 секунд. Время ожидания сообщений в очереди неограниченно. Найти характеристики СМО:
Ротк – вероятность отказа передачи сообщений;
Q – относительную пропускную способность ветви связи;
А – абсолютную пропускную способность ветви связи;
Z – среднее число занятых каналов;
Lоч – среднее число сообщений в очереди;
Тож – среднее время ожидания;
Тсист – среднее суммарное время пребывания сообщений в очереди и передачи по ветви связи.
Решение:
![]()
![]()
Найдём среднюю относительную нагрузку на один канал:
![]()
Найдём вероятности состояния СМО:
Вероятность свободного состояния четырёх каналов:
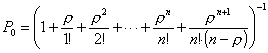
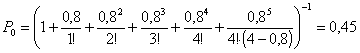
Вероятность занятости одного канала:
![]() ;
; ![]() ;
;
Вероятность занятости двух каналов:
![]() ;
; ![]() ;
;
Вероятность занятости трёх каналов:
![]() ;
; ![]() ;
;
Вероятность занятости четырёх каналов:
![]() ;
; ![]() .
.
Абсолютная пропускная способность А = l = 8 сообщений в секунду, то есть она будет равна интенсивности поступления сообщений в следствии того, что очередь может быть бесконечной, а интенсивность поступления заявок меньше интенсивности их передачи по четырёхканальной ветви связи.
Относительная пропускная способность Q будет равна единице.
Среднее число занятых каналов связи:
![]()
Вероятность отказа приёма сообщения для передачи по ветви связи в следствии того, что r/n < 1 будет равна нулю.
Среднее число сообщений определим по формуле:
![]() ,
,
![]()
Среднее время ожидания в очереди:
![]() с.
с.
Среднее суммарное время пребывания сообщения в очереди на передаче по ветви связи:
![]() с
с
Теория сетей связи: Учебник для вузов связи./ Рогинский В. Н., Харкевич А. Д., Шнепс М. А. и др.; Под ред. В. Н. Рогинского. – М. Радио и связь, 1981. –192с.
Вентцель Е. С. Исследование операций. – М.: Советское радио, 1972. –552с.
Вентцель Е. С. Теория вероятностей. –М.: Наука, 1969. –576с.
Клейнрок Л. Вычислительные системы с очередями. –М.: Мир,1976. –600с.
Методическое пособие и задание на контрольную работу по дисциплине «Теория телетрафика»; Михеенко. В. С. – 1998.
Похожие работы
аочник: Дударев А.Ю. Преподаватель: Абилов А.В. ИЖЕВСК 2001 Задание №1., где NN – номер варианта, =5,55. , где NN – номер варианта, . , .а) - распределение Бернулли. Среднее число занятых линий: . Дисперсия: . б) - распределение Пуассона. Среднее число занятых линий и дисперсия: .в) - распределение Эрланга. Среднее число занятых линий: . Дисперсия: Задание №2., , . 3. ...
... них 10 час. – обзорные лекции, 4 час. –практические занятия, 6 час. – лабораторные работы на ЭВМ. Рабочая программа курса «Моделирование систем радиосвязи и сетей радиовещания». СОДЕРЖАНИЕ ДИСЦИПЛИНЫ 1 Введение Цели и задачи дисциплины. Основные понятия теории моделирования систем. Использование моделирования при исследовании и проектировании сетей ...
... . Требования к сельским коммутационным станциям : Требования, предъявляемые к используемому для модернизации сельских районов коммутационному оборудованию, в значительной степени обусловлены не только географическими особенностями и исторически сложившейся структурой сельских телефонных сетей (СТС), но и принятыми алгоритмами обслуживания вызовов для обеспечения приоритета междугородных ...
... из сети провести крайне трудно, так как эти потоки являются сложными благодаря воздействию отрицательных заявок и из-за нелинейности уравнений трафика. 2. ОТКРЫТЫЕ СЕТИ С МНОГОРЕЖИМНЫМИ СТРАТЕГИЯМИ ОБСЛУЖИВАНИЯ И ИНФОРМАЦИОННЫМИ СИГНАЛАМИ ДВУХ ТИПОВ В 1 исследовалось стационарное распределение марковского процесса, описывающего открытую сеть с многорежимными стратегиями обслуживания и ...
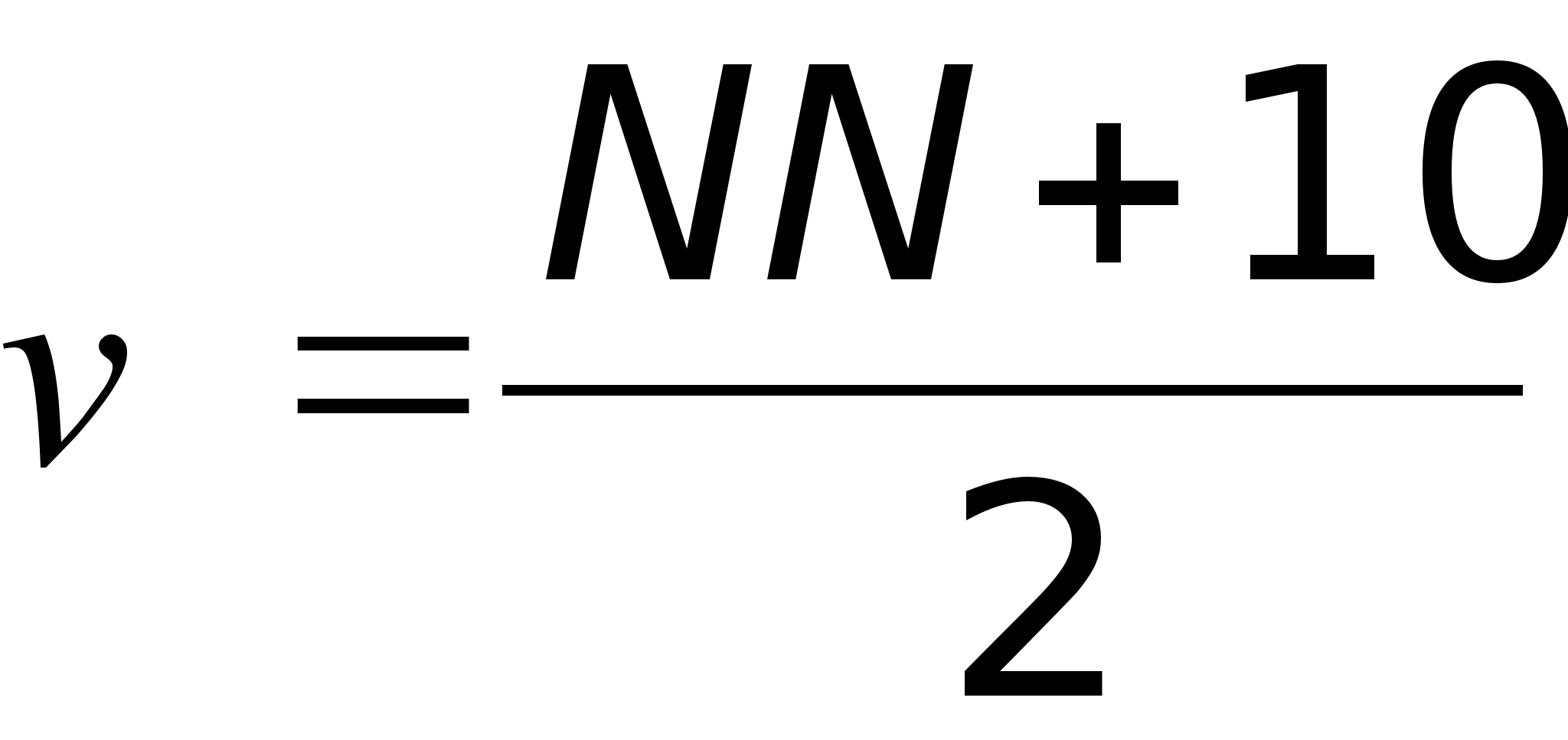
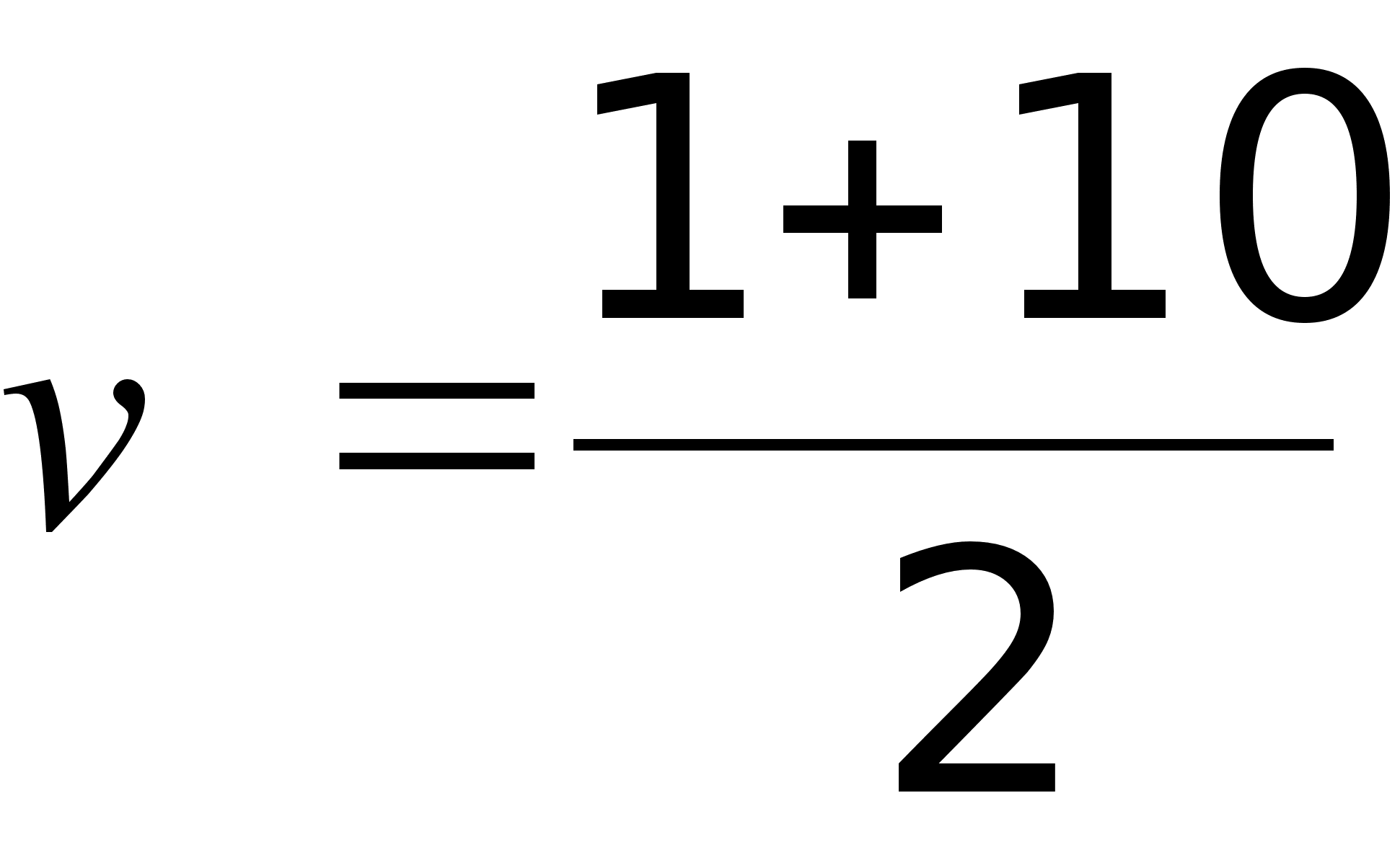
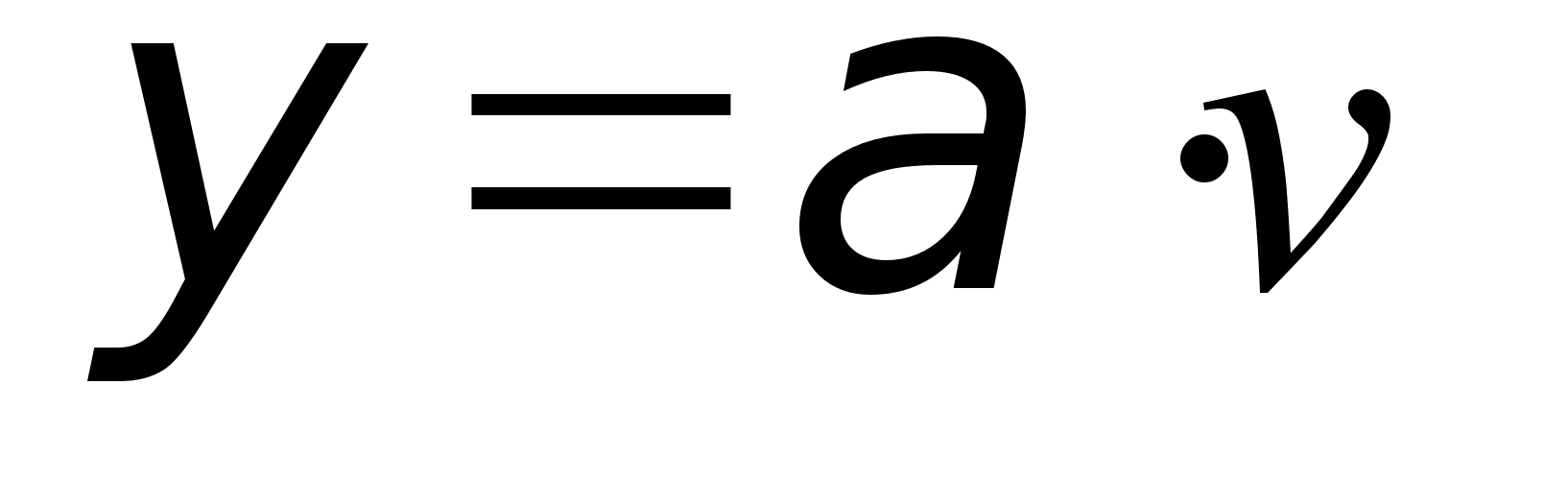
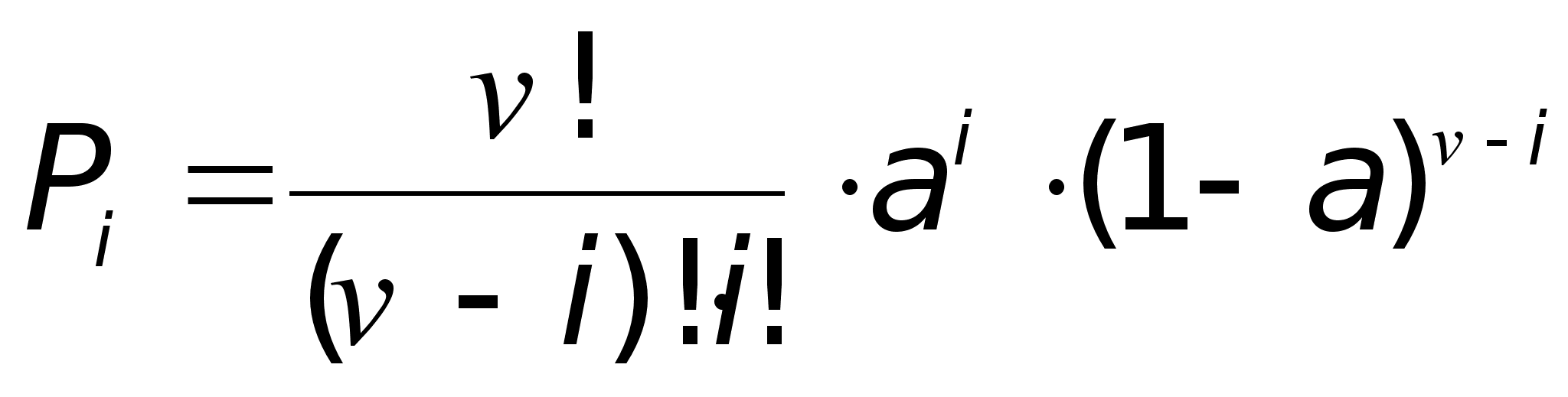

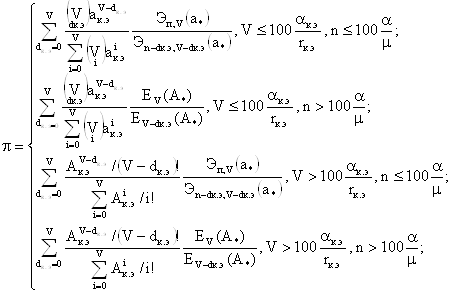

0 комментариев