Кузнецов Ю.Н.
Уравнение симметрийно-физического перехода в электромагнитных явлениях.
В математических моделях природных явлений реальным геометрическим симметриям описываемых объектов соответствуют геометрические симметрии тензорных величин. Чем ниже ранг тензора, тем выше степень его предельной геометрической симметрии.
Отобразим симметрийно-физический переход в локальной электродинамике посредством рангового преобразования. С этой целью умножим на безразмерный
4-вектор известное максвелловское уравнение
![]()
![]()
![]() . (1)
. (1)
В результате двумя уравнениями с тензорами первого и нулевого рангов описываются разные симметрии физически наполненных геометрических величин.
Соответственно, разные свойства у двух видов источников и их полей, разные причинно-следственные связи у одной и той же природной сущности.
Сведём к нулю в правом уравнении производную по времени. В итоге получаем дифференциальную форму записи известной электростатической теоремы Гаусса
ÑÑ![]() . (2)
. (2)
И новое гауссоподобное дифференциальное уравнение для более симметричной локальной магнитостатики с потенциальным магнитным полем, образуемым безнаправленными (в общем случае – бесконечно малыми сферическими) центрально-симметричными токами зарядов
Ñ Ñ ![]() . (3)
. (3)
Приравнивая нулю источники поля в левом и правом уравнениях равенства (1), получаем математическое описание симметрийно-физического перехода для ЭМВ в пустом пространстве. Перехода поперечных ЭМВ в продольные.
В общем случае ранговое преобразование описывает ступенчатый переход к другой геометрической симметрии тензорных величин, сопровождаемое ступенчатым
изменением их физического наполнения.
В случае практической реализации симметрийно-физического перехода в каком-либо конкретном явлении ранговое преобразование представляет собой его теоретическую модель.
Оно может использоваться в предсказательных целях, являясь разновидностью метода математической гипотезы.
Построение математической модели безвихревой электродинамики. В результате анализа центрально-симметричной магнитостатики [1] была получена формула, связывающая потенциал и напряжённость стационарного магнитного поля
![]() (4)
(4)
Переходя к описанию переменного поля, посредством умножения обеих частей
равенства (4) на оператор ![]() , имеем формулу
, имеем формулу
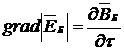 , (5)
, (5)
отображающую локальное явление электромагнитной индукции вне вещественного источника.
Используя принцип перестановочной двойственности [2], трансформируем формулу (5) в запись явления магнитоэлектрической индукции
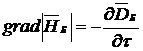 . (6)
. (6)
Подставляя в формулу (5) отношение (1) , а в формулу (6) равенство
![]() (7)
(7)
соответственно имеем
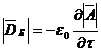 , (8)
, (8)
![]() . (9)
. (9)
Две пары равенств (4), (8) и (7) ,(9) представляют собой 3 – мерные компоненты двух 4 – мерных уравнений
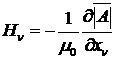 (10)
(10)
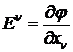 , (11)
, (11)
где
![]() (12)
(12)
![]() (13)
(13)
являются исходными элементами математической модели гипотетической безвихревой электродинамики – магнитным и электрическим 4–векторами напряжённости поля.
Дальнейшее построение сводится к применению к исходным 4-векторам универсальных операторов таким же образом, как это делается в известной модели.
Первым действием записываются уравнения для пустого пространства
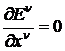 , (14)
, (14)
![]() . (15)
. (15)
Вещественные источники вводятся в (14),(15) как естественное дополнение, приводящее их к максвеллоподобному виду
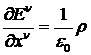 , (16)
, (16)
![]() (17)
(17)
С одной стороны, модуль вектора плотности тока применяется в (17) вынужденно для его совмещения со скалярным уравнением. С другой – он является адекватным математическим описанием бесконечно малой центрально – симметричной сферической (осе
вой Jx=0, аксиальной Jx=0, Jу=0) системы противонаправленных токов зарядов, не имеющей выделенного посредством вектора направления.
Прежде, чем объединить уравнения (16), (17), необходимо согласовать размерности. С этой целью левая и правая части уравнения (16) умножаются на ![]() .
.
В результате суммирования имеем
![]() , (18)
, (18)
где 4-скаляр источника
![]() , (19)
, (19)
![]() . (20)
. (20)
Введя суммарный 4-вектор
![]() , (21)
, (21)
получаем
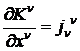 (22)
(22)
Умножая обе части уравнения (22) на оператор ![]() с минусовым знаком перед ним, имеем аналог известным уравнениям Даламбера относительно напряженностей безвихревого электромагнитного поля
с минусовым знаком перед ним, имеем аналог известным уравнениям Даламбера относительно напряженностей безвихревого электромагнитного поля
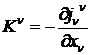 . (23)
. (23)
Уравнение, связывающее между собой потенциалы и напряженности, строится из формул (10) ,(11), (21). В итоге имеем
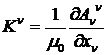 . (24)
. (24)
При его подстановке в уравнение (22) получается равенство, связывающее вещественный источник с потенциалами поля
![]() , (25)
, (25)
где
![]() , (26)
, (26)
![]() . (27)
. (27)
Применение к двум парам 3- мерных составляющих уравнения (24)
математических построений по аналогии с [3] выявляет в плоском приближении продольно-скалярную электромагнитную волну с электрической
- ![]() (28)
(28)
и магнитной
![]() (29)
(29)
синфазными составляющими.
Математическая модель безвихревой электродинамики характеризуется скалярно-векторной структурой своих уравнений.
Основополагающие уравнения безвихревой электродинамики сведены в таблице 1.
Таблица 1
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
Возвращаясь к равенству (1) отметим, что его правая сторона совпадает с
уравнением из таблицы1. Частичную инвариантность этого скалярного уравнения только по отношению к пространственным поворотам следует понимать в том смысле, что оно «извлечено изнутри» полностью инвариантного максвелловского.
Плоская поперечно-векторная ЭМВ занимает в 4-мерном пространстве-времени две взаимно ортогональные пространственные координаты. Свободными для полевых компонент общей ЭМВ остаются одна пространственная (продольная) и временная (скалярная) координаты, которые они и занимают сохранившимися скалярными модулями, и новыми продольными векторами.
Наглядным образом скалярных компонент уравнений безвихревой электродинамики являются соответствующие векторные диаграммы нуль-векторов. Знак скаляра предлага-
ется положительным для расходящихся противонаправленных векторов, отрицательным – для сходящихся.
Сопоставление 3-мерных компонент основополагающих уравнений двух электродинамикчески представлены в таблице 2.
Таблица 2
| Компоненты уравнений безвихревой электродинамики | Компоненты уравнений вихревой электродинамики |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
Электромеханическая связь. Для вывода электромеханической связи образуем две пары 3 – мерных уравнений
![]() , (30)
, (30)
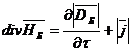 (31)
(31)
и
![]() , (32)
, (32)
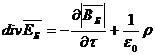 . (33)
. (33)
Просуммируем их попарно, предварительно умножив каждое соответственно на ![]() ,
,
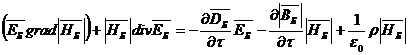 . (34)
. (34)
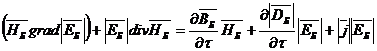 , (35)
, (35)
Используя формулу векторного анализа
![]() , (36)
, (36)
в итоге получим
![]() , (37)
, (37)
![]() . (38)
. (38)
Из (38) следует
![]() (39)
(39)
Вихревая и безвихревая теоретические модели имеют одинаковые математические каркасы, единообразно связывающие собой электро- и магнитостатику, индукционные и электроволновые процессы.
При построении уравнений безвихревой электродинамики идея симметрийно-физических переходов привлекалась только посредством равенства (4). Полученный результат в целом представляет собой систему 4-мерных уравнений, более симметричных по отношению к максвелловским. В частности это подтверждается ранговым преобразованием (1).
В заключение можно констатировать, что вихревая и безвихревая электродинамики описывают разные стороны одной и той же природной сущности. А различаются эти стороны между собой своими геометрическими симметриями.
Список литературы1.Кузнецов Ю.Н. Безвихревая электродинамика. Часть1.Потенциальное магнитное поле
2. Фёдоров Н.Н. Основы электродинамики. М. «Высшая школа», 1980 г., стр.48.
3..Ландау Л.Д., Лифшиц Е.М. Теория поля. М., «Наука», 197
Похожие работы
... однонаправленными стационарными токами в паре рамок (Рис.4) магнитное охлаждение заметным образом не проявлялось. Опытная регистрация эффекта переменного потенциального магнитного поля. Из математической модели безвихревой электродинамики [ 2 ] имеем следующую формулу для вычисления ЭДС, образуемой в проводнике посредством бесциркуляционного магнитного поля ε , ...
... - чески в суммирующем кабеле наряду с продольными имелось некоторое количество (15% …35%) поперечных ЭМВ. В случае частичной нуль-векторной полевой ситуации общая электромагнитная энергия переносится поперечными и продольными ЭМВ, занимающими в пространстве- времени четыре координаты. Если комбинированная ЭМВ входит в резонансный контур, то образующийся в замкнутом контуре замкнутый ток ...
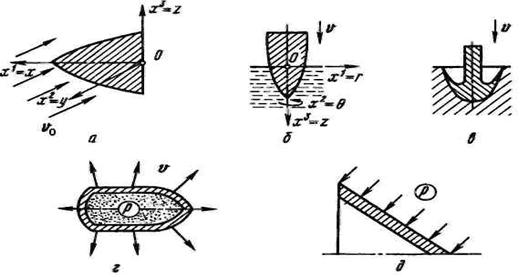
... и трещинами. Решение построено на использовании теории функции комплексного переменного и удовлетворении граничным условиям методом наименьших квадратов. 1 Термодинамические основы термоупругости 1.1 Термоупругость Основное уравнение термоупругости. При термическом расширении изотропное тело деформируется таким образом, что компоненты деформации отнесенные к системе прямоугольных осей ...
... уравнений магнитного поля для плоской поперечной магнитной волны показал, что теория магнетизма дает описание поперечных радио- и световых волн более простыми средствами, чем теория электромагнетизма, но, в отличии от последней, обладает непротиворечивой физической моделью процесса распространения магнитных волн. 2. Расчет Э.Д.С. магнитной индукции во вторичной обмотке катушки индуктивности при ...
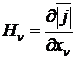
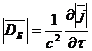
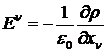



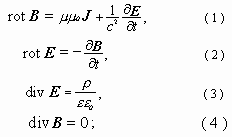
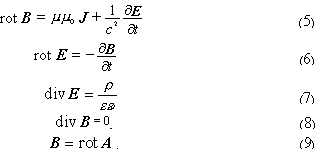
0 комментариев