Введение в физику черных дыр

СОДЕРЖАНИЕ

Особенности сил тяготения
Что такое черная дыра?
Краткие сведения об общей теории относительности Эйнштейна
Сферически-симметричный гравитационный коллапс
Вращающиеся и заряженные черные дыры
Общие свойства черных дыр
Эволюция звезд и черные дыры
Как обнаружить черную дыру?
Энергетика черных дыр
Квантовые эффекты в черных дырах
Первичные черные дыры
Черные дыры, термодинамика, информация
Что внутри черной дыры?
Вместо заключения: проблемы и гипотезы
Литература

ОСОБЕННОСТИ СИЛ ТЯГОТЕНИЯ

Одним из наиболее удивительных предсказаний теории тяготения Эйнштейна является возможность существования черных дыр — компактных массивных объектов, обладающих столь сильным гравитационным полем, что никакие физические тела, никакие сигналы не могут вырваться из них наружу. И хотя черные дыры с полной достоверностью пока еще не открыты, имеется немало причин, по которым они привлекают к себе в последние годы пристальное внимание ученых. По-видимому, наиболее важной из них является то, что обнаружение черных дыр имело бы значение, далеко выходящее за рамки астрофизики, поскольку речь идет не об открытии еще одного, быть может, довольно удивительного астрофизического объекта, а о проверке правильности наших представлений о свойствах пространства и времени в сильных гравитационных полях.

Теоретические исследования свойств черных дыр и возможных следствий гипотезы об их существовании особенно интенсивно развивались последние 15 ,Лет. Наряду с изучением тех особенностей черных дыр, которые важны для понимания их возможных астрофизических проявлений, теоретические исследования позволили обнаружить ряд неожиданных закономерностей, ирису-1Дих физическим взаимодействиям с участием черных Дыр и установить глубокую связь физики черных дыр. С такими на первый взгляд далекими областями, как Термодинамика и теория информации. О черных дырах, их месте в астрофизике и об их удивительных свойствах и пойдет речь ниже.

Самое “слабое” взаимодействие. За возникновение черных дыр ответственны силы тяготения, вероятно, самого удивительного из всех известных физике взаимодействий, Начнем с того, что гравитационное взаимодействие — самое слабое. О его слабости можно судить,

например, по такому факту. Если принять за единицу энергию ядерного (сильного) взаимодействия между двумя протонами на расстоянии порядка размера протона, 2*10-14 см, то энергия их электромагнитного взаимодействия будет в e2/-hc~1/137 Раз (-h - аш с чертой) меньше, энергия слабого взаимодействия достигает 10-5, а энергия гравитационного притяжения составит всего лишь 10-38. И несмотря на это, силы тяготения не только были открыты первыми, а закон Ньютона, описывающий эти силы, послужил отправной точкой для описания других взаимодействий, но и в подавляющем числе явлений в астрофизике и космологии гравитация играет основную роль. Причина этого состоит в том, что тяготение обладает рядом замечательных свойств, ведущих к его многократному усилению, не будь которого, это взаимодействие скорее всего вообще не было бы открыто. Что же это зa свойства?

Гравитационные силы — дальнодействующие. Свойство дальнодействия означает, что сила, действующая на пробную частицу со стороны тела, создающего поле, медленно, по степенному закону, уменьшается с расстоянием. Благодаря этому свойству пробная частица испытывает тяготение со стороны всех частей массивного тела, в том числе и достаточно от нее удаленных. Этим свойством наряду с тяготением обладает Электромагнитное взаимодействие, в то время как сильное и слабое взаимодействия являются короткодействующими и имеют малые радиусы действия. Физическая причина такого различия состоит в том, что кванты, переносчики сильного и слабого взаимодействия, обладают ненулевой массой покоя, что приводит к экспоненциально быстрому убыванию силы на расстояниях, превышающих комптоновскую длину волны lambda = -h/тс этих квантов. Радиусы действия сильного и слабого взаимодействий ~ 10-13 и 10-17 см соответственно. Кванты электромагнитного поля, фотоны, и кванты гравитационного поля, гравитоны, — частицы безмассовые, и сила взаимодействия между парой электрических зарядов или массивных тел убывает по известному степенному закону: сила обратно пропорциональна квадрату расстояния.

Гравитационные силы имеют один знак. Между электромагнитным и гравитационным взаимодействиями имеется, однако, существенное отличие. В природе существуют электрические заряды двух видов: положи-

тельные и отрицательные, причем одноименные заряды отталкиваются. Это приводит к тому, что в макроскопических телах электрический заряд обычно практически скомпенсирован, в противном случае они были бы разорваны на части мощными силами электростатического отталкивания. Более того, при отсутствии, сторонних сил процессы в системах с заряженными телами протекают таким образом, чтобы уменьшить потенциальную энергию, при этом заряды противоположных знаков будут компенсироваться. Все это приводит к тому, что в естественных условиях электрический заряд макроскопических тел оказывается пренебрежимо малым,

Напротив, “заряды тяготения” — массы — всегда имеют один и тот же знак, причем они не отталкиваются, а притягиваются друг к другу. При этом чем тело массивнее, тем оно более устойчиво относительно “развала”. Для гравитационного взаимодействия характерен следующий, механизм самоусиления: массивное тело притягивает к себе вещество, падающее вещество увеличивает массу тела и, следовательно, его способность. Притягивать. Силы тяготения, ничтожно малые для отдельных элементарных частиц, суммируясь при составлении из них макроскопического тела, могут достигать огромной величины, вырастая в космическом масштабе, в могучий, нередко определяющий фактор. При этом малость константы гравитационного взаимодействия компенсируется большой величиной гравитационного заряда. Описанный выше механизм самоусиления приводит к тому, что в тех масштабах, в которых тяготение доминирует над другими взаимодействиями, однородное распределение вещества оказывается неустойчивым и рост случайных неоднородностей вызывает развитие, в частности, таких наблюдаемых структур, как планеты, звезды, галактики и скопления галактик.

Универсальность гравитационного взаимодействия. Гравитационное взаимодействие обладает еще одним, крайне важным, отличительным свойством — оно универсально. Для каждого из остальных, перечисленных выше взаимодействий существуют нейтральные частицы, тогда как все объекты, существующие в природе (включая и поля), порождают гравитационное поле. В роли гравитационного заряда выступает полная масса т системы, которая, как учит специальная теория

относительности, связана с полной энергией системы Е соотношением т=Е/с2. Именно поэтому все объекты природы, обладая энергией, непременно участвуют в гравитационном взаимодействии. “Весит”, в частности, и само гравитационное поле, что приводит к существенной нелинейности уравнений Эйнштейна, описывающих тяготение.

ЧТО ТАКОЕ ЧЕРНАЯ ДЫРА?

Вывод Лапласа. Гравитационное поле тем сильнее, чем больше масса тела и чем меньше размер области пространства, в которой это тело сосредоточено. Еще в 1795 г. великий французский математик Пьер-Симон Лаплас, исследуя распространение света в поле тяготения, пришел к выводу, что в природе могут встречаться тела, абсолютно черные для внешнего наблюдателя. Поле тяготения таких тел настолько велико, что не вы пускает наружу лучей света. На языке космонавтики 9то означает, что вторая космическая скорость была бы больше скорости света с. Вывод Лапласа основывался на следующем рассуждении. Для того чтобы преодолеть гравитационное притяжение, создаваемое телом с массой М, и улететь на бесконечность, пробное тело на поверхности этого тела радиуса R должно обладать скоростью v, такой, что v2/2>=GM/R. Считая, что это соотношение применимо для света, мы вместе с Лапласом приходим к заключению, что если масса объекта сосредоточена в области с радиусом, меньшим так называемого гравитационного радиуса тела? Rg :Rg= =2GМ/с2~=~1,5-10-28 М (масса М измеряется в граммах, Rg — в сантиметрах), то даже свет не выйдет за пределы этой области. Для Солнца гравитационный радиус — около 3 км, для Земли — порядка 1 см.

Теория Эйнштейна — ключ к проблеме черных дыр. Вывод Лапласа, строго говоря, является ошибочным, поскольку он основан на классической механике и 'теории тяготения Ньютона. В действительности, однако, нельзя пользоваться ни той, ни другой: распространение света подчиняется законам релятивистской механики, а сильное поле тяготения, т. е. поле, гравитационный потенциал которого phi = GM/R в единицах с2 порядка единицы: phi/с2~1, описывается общей теорией относительности. Тем не менее, как это иногда случается в истории

науки, обе “ошибки” Лапласа точно скомпенсировали друг друга и вывод о невозможности выхода световых сигналов из-под гравитационного радиуса оказался совершенно правильным. Более того, связанный со специальной теорией относительности и справедливый в общей теории относительности запрет на существование в природе сигналов, переносящих информацию со скоростью, большей скорости света, придал утверждению о невозможности получения какой-либо информации о событиях, происходящих под гравитационным радиусом, еще более категорический смысл.

..Подобное тело, сжатое до размера своего гравитационного радиуса, получило название черной дыры, а границу черной дыры, т. е. поверхность, ограничивающую область, откуда невозможен выход сигналов, стали называть горизонтом событий. Хотя вывод Лапласа о возможности существования черных дыр сохраняется и в общей теории относительности Эйнштейна, само описание этого объекта имеет существенные отличия. Прежде чем перейти к точному определению черных дыр и к рассказу об их удивительных свойствах, необходимо хотя бы несколько слов сказать об эйнштейновской теории гравитации.

КРАТКИЕ СВЕДЕНИЯ ОБ ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА

Принцип эквивалентности. Общая теория относительности, в окончательной форме сформулированная Эйнштейном в 1915 г., возникла в результате попытки построения релятивистского обобщения теории тяготения Ньютона, т. е. приведения теории Ньютона в соответствие с принципом конечности скорости распространения взаимодействия и с законами специальной теории относительности. Исходным пунктом для построения общей теории относительности явился принцип эквивалентности инертной и гравитационной масс. Согласно этому принципу отношение гравитационной массы mгр, определяющей силу F, действующую на тело в гравитационном поле напряженности T:F = mгрГ, к инертной массе тин, связывающей силу F и величину вызываемого ею ускорения a:F = mинa, не зависит от свойств и состава тела. Поэтому ускорение пробного тела в трави-

рационном поле определяется только напряжённостью поля в точке, где тело находится. Иными словами; "в гравитационном поле зависимость от времени положения пробного точечного тела, его мировая линия, однозначно определяется начальным положением тела и его скоростью. Тем самым задача изучения движения частиц в гравитационном поле сводится к изучению геометрии мировых линий. В отсутствие поле тяготения мировые линии движения свободных частиц являются прямыми, т. е. кратчайшими, линиями между произвольной парой точек, лежащих на них. Оказывается, что при наличии гравитационного поля мировые линии пробных тел тоже можно считать “кратчайшими”, если только отказаться от предположения о том, что простр?а нет вовремя — плоское, и подобрать его геометрию соответствующим образом.

Гравитация как геометрия. Геометрия искривленного пространства определяется заданием расстояния между произвольной парой близких точек этого пространства. Тем самым определяется понятие длины любой кривой в таком пространстве. “Кратчайшие” кривые Лосят название геодезических. В заданных координатах квадрат расстояния ds2 между парой близких точек 'с координатами хмю и х'+dxмю в точке х определяется следующим образом: ds2 = gмюню (х)dхмю dхню, . Набор функций gмюню , задающий в каждой координатной системе pdc-стояние между близкими точками, называется метрикой. В плоском пространстве-времени координаты можно выбрать так, что функции gмюню постоянны во всем пространстве-времени и метрика имеет вид: ds2 = этамюню dxмюdx' -= (тождественно=) —C2dt2 + dx2 + dy2 + dz2. В общем случае это невозможно. Самое большее, чего удается достичь за счет выбора координат, это добиться совпадения метрики gмюню (х) В Окрестности ПРОИЗВОЛЬНОЙ ТОЧКИ x0 С этамюню с точностью до величин второго порядка малости.

Предположим теперь, что в гравитационном поле свободно движется невращающееся пробное тело. Свяжем с ним систему отсчета и, воспользовавшись принципом эквивалентности, постараемся описать в этой системе явления, происходящие в окрестности тела. Прежде всего заметим, что если мы ограничимся областью пространства-времени, размеры которой I много меньше характерной длины L, на которой гравитационное ноле

заметно изменяется, то ускорения всех тел в такой окрестности практически совпадают и относительно выбранной нами системы отсчета такие тела будут двигаться равномерно и прямолинейно. Иными словами, переходом к свободно падающей системе отсчета можно локально исключить гравитационное поле. В такой системе отсчета движение тел подчиняется законам, специальной теории относительности, а отклонение от этих законов тем меньше, чем меньше величина отношения HL,

Строго говоря, сделанный вывод о возможности, две-дения путем перехода к падающей системе отсчета задачи о движении в гравитационном поле к задаче о движении в инерциальной системе отсчета вне поля тяготения, т. е. к задаче специальной теории относительности, непосредственно касается только механических явлений. Заметим, однако, что осуществленная с крайне высокой степенью точности экспериментальная проверка равенства инертной и гравитационной массы { Вариация отношения mгр/mин при выборе различных веществ не превышает величины 10-12. Этот лучший в настоящее время результат был получен в 1971 г. в МГУ в группе В. Б. Брагинского.} позволяет распространить этот вывод на широкий класс немеханических явлений и сделать далеко идущие выводы о характере взаимодействия вещества и физических полей с гравитацией.

Дело в том, что свой вклад в полную энергию системы, а следовательно, и в ее инертную массу, вносят не только механические массы покоя частиц, входящих в состав системы, но и кинетическая энергия, связанная с их движением, а также и потенциальная энергия электромагнитного, сильного, слабого и самого гравитационного взаимодействий частиц друг с другом. Тот факт, что гравитационный заряд, равный гравитационной массе системы, совпадает с ее полной инертной массой, означает, что каждое из взаимодействий дает свой вклад в вес тела.

Объяснить эти экспериментальные результаты можно, лишь предположив, что принцип эквивалентности справедлив не только для механических движений, т. е. что выполняется более общий, так называемый принцип эквивалентности Эйнштейна, гласящий, что результат любого (не обязательно механического) локального эксперимента, выполненного в свободно падающей системе отсчета, не зависит от того, где и когда во Вселенной этот эксперимент был выполнен, и от того, с какой скоростью двигалась система отсчета. Согласно этому принципу для описания взаимодействия любой системы с гравитационным полем достаточно знать закон, управляющий поведением системы в инерциальной системе отсчета. Поведение системы в гравитационном поле, описываемом метрикой gмюню , определяется простым пересчетом с помощью преобразования координат. Эта задача имеет чисто геометрический характер.

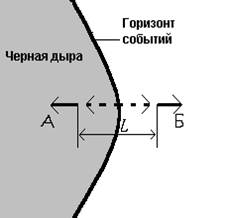
Приливные силы и кривизна пространства-времени. Если гравитационное поле неоднородно, то исключить его путем перехода к падающей системе отсчета сразу во всем пространстве или в конечной, но не очень малой области не удается. Действительно, рассмотрим, например, относительное движение в гравитационном поле Земли двух частиц, расположенных на расстоянии l друг от друга и падающих по радиусу к ее центру (рис. 1). При этом движении частицы 1 к 2 сближаются, ускорение их относительного сближения равно GMl/R3. Частицы 3 и 4 удаляются друг от друга с относительным ускорением 2GMl/R3. Это означает, что при

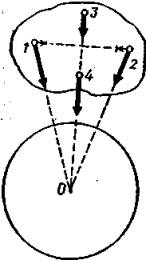движении протяженного тела в неоднородном гравитационном поле в нем возникают так называемые приливные силы, стремящиеся его деформировать. Относительное приливное ускорение пары точек тела пропорционально расстоянию между этими точками и зависит от их взаимного расположения. Тензорный коэффициент пропорциональности характеризует степень неоднородности гравитационного поля и носит название тензора кривизны пространства-времени.

Поскольку гравитационное взаимодействие универсально к не существует “нейтральных” по отношению к нему тел, то оказывается невозможным в чисто гравитационных экспериментах измерить “напряженность” гравитационного поля. Подобные эксперименты позволяют определить только относительные ускорения, т. е. кривизну пространства-времени. Пространство-время является плоским, если его кривизна всюду обращается в ноль. В случае если кривизна не равна нулю, метрика не может быть плоской, однако в окрестности любой точки ее можно привести к виду:

gмюню (x)=etaмюню + (кривизна пространства-t)*(х-x0)2 +(поправки порядка (х—х0)3 )

Уравнения Эйнштейна. Согласно Эйнштейну, кривизна пространства-времени пропорциональна плотности энергии-импульса вещества, порождающего гравитационное поле. Соответствующие уравнения, позволяющие определить метрику по заданному распределению вещества и тем самым восстановить геометрию пространства-времени, носят название уравнений Эйнштейна. В пределе, когда гравитационное поле слабое, т. е. гравитационный потенциал phi (ф) много меньше с2 и движение источника нерелятивистское, уравнения Эйнштейна сводятся к обычному уравнению для гравитационного потенциала в теории Ньютона. Тем самым предсказания теории Эйнштейна для слабых гравитационных полей носят характер малых поправок ~ф/с2 к известным результатам теории Ньютона. Именно эти поправки подвергаются экспериментальной проверке. Результаты всех наблюдений и экспериментов по проверке общей теории относительности, включая такие, как измерение красного смещения и запаздывания световых сигналов в гравитационном поле, измерение сдвига перигелия Меркурия и отклонение лучей света Солнцем, подтверждают эту теорию в области слабого поля, допуская отклонение от нее не более нескольких процентов.

Наиболее радикально отличаются предсказания теории Эйнштейна от ньютоновской теории гравитации в случае, когда гравитационное поле нельзя считать слабым. Качественно новым в этом случае является предсказание теорией Эйнштейна возможности нетривиальных глобальных свойств пространства-времени. Это касается прежде всего космологии, когда рассматриваются, области пространства и интервалы времени порядка-радиуса кривизны пространства-времени. В частности наше пространство может обладать нетривиальной топологией и походить не на плоскость, а на расширяющуюся сферу, являясь замкнутым, имея конечный объем, но не обладая никакими границами.

Возможность существования черных дыр — другое предсказание теории Эйнштейна — связана с появлением нетривиальной причинной структурой, которая проявляется в наличии в пространстве-времени областей, откуда невозможно получение никакой информации наблюдателями, расположенными вне этой области.

Отсутствие экспериментальной проверки теории Эйнштейна в области сильного поля, именно там, где предсказания этой теории носят весьма специальный характер, оставляет в принципе открытой возможность для развития других, отличных от теории Эйнштейна теорий гравитации. За время, прошедшее с момента создания общей теории относительности, такие попытки предпринимались неоднократно. Практически все рассматриваемые в настоящее время модификации теории гравитации принимают принцип эквивалентности и являются метрическими, т. е. описывают действие гравитационного поля на вещество в терминах искривленного пространства-времени. Основные расхождения касаются формы уравнений самого гравитационного поля:

Новая теория гравитации получает право на жизнь лишь после того, как подтверждается ее пригодность для описания результатов экспериментов в слабом гравитационном поле. Общим для большинства из развитых вариантов оказалось предсказание возможности су* шествования отрицательных энергий, так что при гравитационном излучении в двойной системе в таких теориях предсказывается увеличение (а не уменьшение!) расстояния между телами. Такие варианты, на наш взгляд, не следует считать разумными. И хотя до сих пор теория Эйнштейна является непревзойденной по красоте, строгости и экономности предпосылок, лежащих в (fee основании, и большинство физиков считают ее справедливой, в роли окончательного судьи в этом вопросе должен выступить опыт. Именно поэтому обсуждение свойств черных дыр и возможности наблюдения их с целью проверки предсказаний теории Эйнштейна в сильных гравитационных полях приобретают такое важное значение. Ниже, рассказывая о черных дырах, мы опираемся на результаты, полученные в рамках общей теории относительности.

Диаграммы пространства-времени. Исследование свойств гравитационного поля естественным образом разбивается на несколько этапов. Во-первых, необходимо найти решение уравнений Эйнштейна для интересующего нас случая. Не последнюю роль при этом играет удобный выбор координатной системы. При попытке наглядного изображения свойств решения уравнения Эйнштейна возникает проблема, как отразить свойства четырехмерного пространства-времени, да к тому же еще искривленного, на плоском рисунке. К счастью, многие из интересных решений обладают симметрией, т. е. метрика не зависит существенным образом от одной или нескольких переменных, и не теряя общности, можно изобразить на рисунке трехмерное или даже двух мерное сечение такого пространства. Для того чтобы на подобной диаграмме пространства-времени отразить существенные свойства метрики, удобно показать расположение локальных световых конусов, соответствующих данной метрике. Такой локальный световой конус с вершиной в точке хмю является геометрическим местом точек -хмю + dxмю близких к хмю и удовлетворяющих условию gмюню (x)dxмю- dxню = 0. Образующие локального светового конуса изображают движение световых лучей. Пробным массивным частицам соответствуют линии, проходящие через вершину внутрь светового конуса. Картина рас положения локальных световых конусов позволяет не только ответить на многие вопросы, связанные с особенностями движения в найденном гравитационном поле; но и дает ясное представление о причинной структуре пространства-времени.

СФЕРИЧЕСКИ-СИММЕТРИЧНЫЙ ГРАВИТАЦИОННЫЙ КОЛЛАПС

Черная дыра (строгое определение). На рис. 2 представлена диаграмма пространства-времени, изображающая процесс возникновения черной дыры в результате самопроизвольного сжатия — гравитационного коллапса массивного тела сферической формы. Решение, описывающее гравитационное поле вне такого тела, было получено в 1916 г. К. Шварцшильдом, и поэтому часто не вращающуюся и незаряженную черную дыру, описываемую этим решением, называют “шварцшильдовской”, Диаграмма построена на основе этого решения, и расположение локальных световых конусов на ней позво

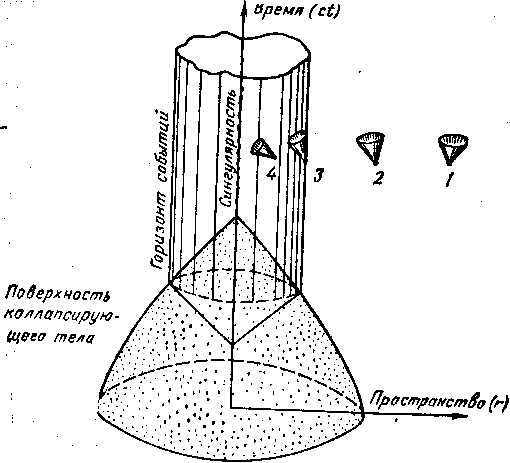
Рис. 2. Диаграмма пространства-времени при сферическом ' коллапсе. Достаточно массивное тело с течением времени : сжимается под действием сил тяготения, пересекает горизонт Событий и в конце концов сжимается в точку. Цифрами обозначены локальные световые конуса. Сигнал из точек 1 и 2 может дойти до внешнего наблюдателя, из точек 3 и 4, т. е. из-под гравитационного радиуса, не может

лдет судить о характере движения пробных частиц и лучей, света в гравитационном поле черной дыры. Действие гравитационного поля проявляется в том, что наклон локальных световых конусов к центру тем больше, чем ближе к центру находится вершина конуса. На поверхности гравитационного радиуса r=Rg=2GM/c2 наклон локального светового конуса (он обозначен цифрой 3 на рисунке) настолько велик, что луч света, идущий наружу, увлекаемый действием мощного гравитационного поля, не может выйти к отдаленному наблюдателю и остается все время на одном и том же расстоянии от центра, равном гравитационному радиусу. Под гравитационным радиусом гравитационное поле вырастает до такой величины, что оно заставляет любые частицы и свет двигаться только в направлении центра.

Поэтому область, лежащая под гравитационным радиусом, оказывается невидимой для любого наблюдателя, покоящегося снаружи. Эта область получила название черной дыры.

Рассматриваемый нами случай — коллапс сферического тела — является простейшим. Черные дыры могут образовываться и в более общих ситуациях, при коллапсе несферических или вращающихся тел. Для образования черной дыры тело должно сжаться так, чтобы его максимальный размер не превосходил величины порядка гравитационного радиуса. Возникновение черной дыры означает, что гравитационное поле возросло до такой величины, что удерживает в ограниченной области пространства все частицы и световые лучи и не дает им вылететь наружу. В соответствии с этим черной дырой в самом общем случае называют область пространства-времени, откуда невозможен выход никаких сигналов к отдаленному наблюдателю. Граница невидимой для внешнего наблюдателя области получила название горизонта событий. Линии, образующие поверхность горизонта событий, совпадают с мировыми линиями пробных световых лучей.

Наличие резкой границы принципиально отличает черную дыру в теории Эйнштейна от “лапласовой черной дыры”. В последнем случае любые захваченные световые лучи, испущенные наружу, прежде чем начнут падать внутрь немного отойдут от центра.

Гравитационный коллапс с точки зрения падающего наблюдателя. Картина коллапса существенно зависит от того; падает ли наблюдатель вместе с коллапсирующмй телом или же покоится на большом расстоянии от него. В первом случае наблюдатель, находясь на поверхности Сжимающегося тела, не отметит никаких качественных особенностей при переходе вещества через гравитационный радиус. Он будет продолжать регистрировать непрерывное возрастание плотности вещества и приливных сил. Приливные силы будут растягивать тела в направлении падения и сжимать их в поперечном направлении. Поэтому, если мы хотим, чтобы наблюдения продолжались как можно дольше, надо позаботиться о том; чтобы сделать наблюдателя или заменяющий его прибор из чрезвычайно стойкого материала. Однако и в этом случае им не удается спастись от разрыва, поскольку, начиная с некоторого момента, приливные силы станут больше сил, удерживающих электроны в атомах. При падении в черную дыру с массой порядка солнечной это произойдет на расстоянии в несколько десятков микрон от центра. Еще ближе к центру приливные силы превзойдут ядерные.

После попадания под гравитационный радиус движение до центра займет по часам падающего наблюдателя время порядка Rg /с. Для черной дыры солнечной массы это время составляет 10-5 с. Момент пересечения гравитационного радиуса сопутствующий наблюдатель может установить следующим образом. Представим себе, что время от времени этот наблюдатель заставляет вспыхнуть поверхность коллапсирующего тела и измеряет, как изменяется площадь поверхности сферического фронта выходящей волны. Пересечению поверхностью тела горизонта событий соответствует момент, начиная с которого, площадь фронта от вспышки не возрастает, А уменьшается.

Остановить коллапс тела, попавшего под горизонт событий, невозможно. Для этого потребовалось бы создать такие условия, при которых частицы поверхности остановили бы свое падение и начали двигаться наружу. Это означает, что скорость их движения должна стать больше скорости света, что противоречит принципу причинности. Согласно общей теории относительности, сжатие вещества, попавшего внутрь черной дыры, продолжается до тех пор, пока его плотность не достигает бесконечно большого значения. При этом образуется сингулярность, т. е. особенность в пространстве-времени, характеризуемая формально бесконечным значением кривизны. Фактически это означает, что в окрестности таких точек нельзя пренебрегать эффектами, которые могли бы привести к модификации уравнений Эйнштейна и которые малы лишь при малых кривизнах. Подобную роль могут играть, например, квантово-гравитационные эффекты.

Картина коллапса с точки зрения удаленного наблюдателя. Удаленный наблюдатель никогда не увидит, что происходит внутри черной дыры. При подходе сжимающейся поверхности тела к гравитационному радиусу увеличивается запаздывание выходящих с поверхности тела наружу сигналов. Поэтому удаленный наблюдатель видит коллапсирующее тело как бы застывающим, а размер его быстро, по экспоненциальному закону, приближающимся к гравитационному радиусу. Выходящие лучи, испытывая возрастающее красное смещение в гравитационном поле, приходят все более и более “покрасневшими”. Мощность излучения быстро падает и за времена порядка Rg/c после сжатия коллапсирующего тела до размера порядка гравитационного радиуса, внешний наблюдатель перестает его видеть: образуется черная дыра. Эта “дыра” действительно черная. Обладая ограниченной энергией, коллапсирующее" тело до пересечения горизонта событий способно излучить на бесконечность лишь конечное число световых квантов, так что после момента выхода наружу последнего излученного кванта из черной дыры больше не выходит никакой информации. Начиная с некоторого момента, оказывается невозможной также попытка получить информацию о сколлапсировавшем теле с помощью посланной вслед этому телу ракеты. Дело в том, что когда эта ракета достигнет гравитационного радиуса, она, конечно же, не обнаружит там сколлапсировавшее тело. В этом смысле воспринимаемая внешним наблюдателем картина застывания тела у гравитационного радиуса напоминает улыбку знаменитого чеширского кота из книги Льюиса Кэрролла “Алиса в стране чудес”, которая оставалась после исчезновения самого кота.

ВРАЩАЮЩИЕСЯ И ЗАРЯЖЕННЫЕ ЧЕРНЫЕ ДЫРЫ

Вращающаяся черная дыра. Эффект Лензе—Тирринга. Вращение тела может существенно изменить ситуацию. Если скорость вращения велика, то возникающие центробежные силы способны помешать коллапсу тела, приводя, например, к его разрыву на части еще до образования черной дыры. Если масса каждой части меньше критической, то этот процесс фрагментации может вообще предотвратить образование черной дыры. К сожалению, очень трудно провести количественные расчеты в подобном случае. Следует, однако, ожидать, что вращение существенным образом изменит картину коллапса, если первоначальный угловой момент J тела превышает величину GM2/c.

Однако если вращение коллапсирующего тела недостаточно велико, чтобы помешать сжатию его до размеров меньше или порядка гравитационного радиуса

(J/(GM2/c)Q = Gc-2R-3[->J — 3->n(->J->n)]. Здесь ->п — единичный вектор направления оси гироскопа. Измеряя угловую скорость прецессии гироскопа в поле вращающейся черной дыры, можно определить ее угловой момент и тем самым угловой момент сколлапсировавшего тела J.

Эргосфера. По мере приближения к вращающейся черной дыре одновременно усиливаются два эффекта: растет поле тяготения и усиливается эффект увлечения. Точное решение уравнений Эйнштейна, описывающее гравитационное поле вращающейся черной дыры, было получено в 1963 г. Роем Керром, Соответствующая этому решению диаграмма пространства-времени изобра жена на рис. 3. Анализ решения Керра показывает, что прежде чем мы достигнем горизонта событий, размер которого определяется выражением r = Rq тождественно= GMc-2(1+ + + sqrt(1-(Jc/GM2)2) ), эффект увлечения возрастает на столько, что оказывается невозможным ему противодействовать2. Это приводит к тому, что внутри поверхности, получившей название предела статичности и определяемой условием

r=Rgтождественно=GM/c2(1+sqrt[1-(Jc/GM2)2cos teta ] )

все тела увлекаются во вращение по направлению вращения черной дыры (teta — угол от оси вращения). Остановить это вращение, не вылетев наружу за предел статичности, невозможно. (Для этого потребовалось бы сообщить телу сверхсветовую скорость.) Область вокруг

----2 При |J|>GМ2/с черная дыра не образуется.

Рис, 3. Диаграмма пространства-времени вращающейся черной дыры

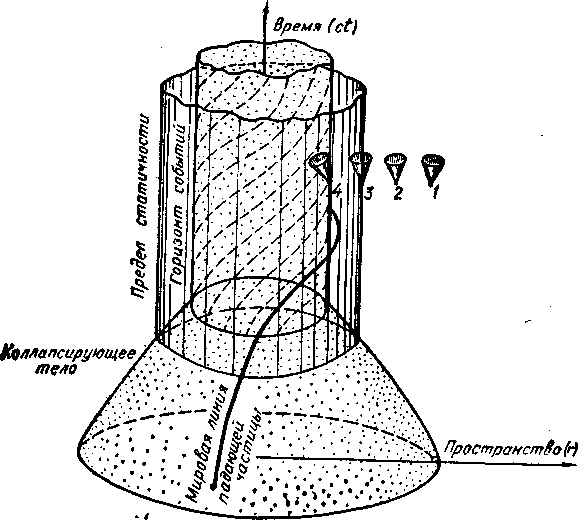
вращающейся черной дыры, лежащая между пределом статичности и горизонтом событий, получила название эргосферы. В отличие от области, лежащей под горизонтом событий, в эргосфере частицы могут двигаться, как приближаясь, так и удаляясь от черной дыры, и, в частности, могут покинуть эргосферу, вылетев наружу. Горизонт событий в общем случае играет роль односторонней мембраны, пропуская частицы и сигналы только в одном направлении — внутрь. -

Угловая скорость вращения черной дыры. Падающий наблюдатель пересекает предел статичности и горизонт событий за конечное время по собственным часам, регистрируя при этом лишь непрерывное возрастание приливных сил. Для внешнего наблюдателя процесс приближения к горизонту -событий как пробной частицы, так и самого коллапсирующего тела затягивается на бесконечно большое (по его часам) время. При этом оказывается, что, подходя к горизонту событий, все те-

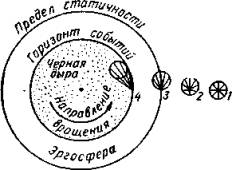Рис. 4. “Вид сверху” по оси вращения на вращающуюся черную дыру. Малые окружности соответствуют положениям фронта волны излучения через малый промежуток времени после испускания волны в точках /, 2, 3, 4. Эффект увлечения в эргосфере настолько велик, что никакое физическое тело не может в ней покоиться относительно удаленного наблюдателя

ла приобретают одну и ту же угловую скорость вращения, равную OMEGA=(J/M)[R2g +(J/Мс)2]-1. Эта величина получила название угловой скорости вращения черной дыры. OMEGA постоянна на поверхности черной дыры. В этом смысле вращение черной дыры напоминает вращение твердого тела. Так же как и при коллапсе невращающегося тела, возрастающее красное смещение при приближении поверхности тела к горизонту и падение по экспоненциальному закону мощности излучения, выходящего к отдаленному наблюдателю, приводят к тому, что через характерные времена порядка Rg /c перестает выходить наружу информация и образуется черная дыра. Заряженные черные дыры. Если коллапсирующее тело обладало электрическим зарядом, то возникающая черная дыра “помнит” об этом. Падение электрического заряда Q в черную дыру приводит к тому, что поток электрического поля через ее поверхность оказывается равным 4piQ в полном соответствии с теоремой Гаусса. Силовые линии электрического поля выходят из черной дыры, и вне ее имеется электрическое поле. Если черная дыра не вращается, то это поле описывается законом Кулона. Вращение заряженной черной дыры с массой М и угловым моментом J приводит к дополнительному появлению дипольного магнитного поля, причем магнитный момент оказывается равным: мю= (Q/M)J. Соответствующее точное решение уравнений Эйнштейна, обобщающее решение Керра на случай, когда черная дыра обладает электрическим зарядом, было получено в 1965 г. в работе группы американских теоретиков во главе с профессором Эзрой Ньюмапом. Как выяснилось позднее, это решение, получившее название решения Керра—Ньюмана, однозначно определяемое тремя параметрами: М - массой, J — угловым моментом и Q —электрическим зарядом, является самым общим из возможных решений, описывающих стационарную черную дыру в пустоте. Геометрические свойства керр-ньюмановской черной дыры весьма сходные с описанными выше свойствами керровской черной дыры.

Поверхность черной дыры при наличии вращения перестает иметь сферическую форму. Площадь поверхности керр-ньюмановской черной дыры равна

A = 4pi [R2g + (J/Mc)2] =4piG2с-4(2M2—Q2/G+.

+ 2Мsqrt[M2—Q2/G—J2c2/G2M2]).

При описании свойств черных дыр важную роль играет так называемая поверхностная гравитация kappa

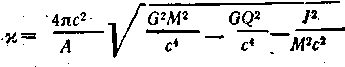
При отсутствии вращения и заряда kappa=c4/GM=GM/R2g Эта величина хaрактеризует “напряженность” гравитационного поля на поверхности черной дыры. Электрический потенциал на поверхности черной дыры равен

ОБЩИЕ СВОЙСТВА ЧЕРНЫХ ДЫР

Несферический гравитационный коллапс. При сжатии сферически-симметричного тела гравитационное поле вне этого тела остается неизменным (статическим). Это утверждение в общей теории относительности известно как теорема Биркгофа. При коллапсе вращающихся тел и тел несферической формы гравитационное поле оказывается нестационарным — происходит излучение гравитационных волн. Черная дыра, возникающая в результате этого коллапса, также нестационарна, т. е. ее форма и размер зависят от времени. Часть гравитационных волн уходит на бесконечность, другая часть поглощается черной дырой, что приводит к увеличению ее энергии. Если черная дыра предоставлена самой себе, то с течением времени процесс излучения гравитационных волн прекращается и черная дыра становится стационарной.

Замечательным оказывается то, что всякая черная дыра, переходя в стационарное состояние, обязательно

превращается в керровскую или в случае, если тело обладало электрическим зарядом, керр-ньюмановскую черную дыру, свойства которой однозначно определяются значениями трех параметров: М — массы, J — углового момента и Q — заряда. После образования стационарной черной дыры все особенности внутреннего строения сколлапсировавшего тела, наличие в нем источников различных полей, кроме электромагнитного, связанного с зарядом Q,становятся недоступными для наблюдения. Подобные черные дыры, обладающие одинаковыми значениями параметров М, J и Q, неотличимы друг от друга. Все остальные характеристики, которыми обладало коллапсирующее тело (такие, как мультипольные гравитационные и электромагнитные моменты, заряды, связанные с другими взаимодействиями (например, сильным и слабым и т. п.), забываются черной дырой.

Физическая причина этого состоит в следующем. Любое физическое поле, обладая энергией, притягивается черной дырой. Поэтому любой элемент объема с таким полем около черной дыры обладает весом. Связанные с полем натяжения проявляются в виде давления со стороны поля на поверхность объема, приводя к “выталкивающей силе”, аналогичной силе Архимеда. Физическое поле может находиться в равновесии около черной дыры, т. е. быть стационарным, если вес поля в любом элементе объема в точности компенсируется “выталкивающей силой”. Если вне черной дыры нет источников полей, то выполнение этого своеобразного “закона Архимеда” оказывается возможным только для таких конфигураций гравитационного и электромагнитного полей, которые отвечают случаю керр-ньюмановской черной дыры. Во всех остальных случаях элемент поля либо “всплывает”, либо “тонет”. После этого процесса перестройки поля, сопровождаемого излучением, черная дыра сохраняет только те характеристики, которые она не способна сбросить при излучении, — массу, угловой момент и электрический заряд.

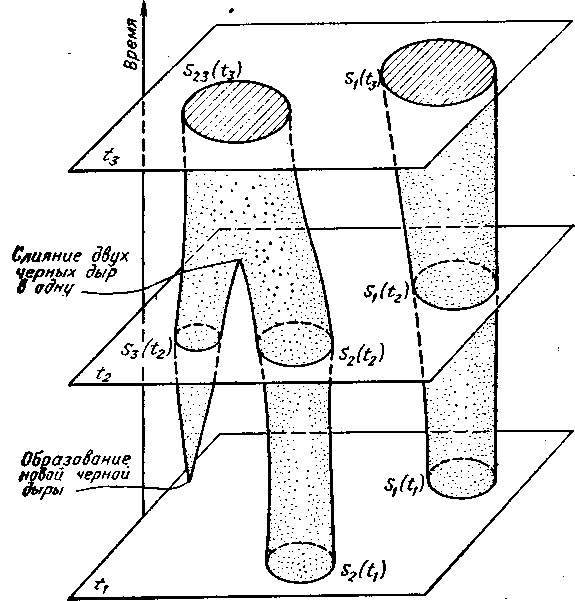
Теорема Хокинга. Хотя детальное описание процесса перестройки поля и превращения черной дыры в стационарную представляет собой довольно сложную задачу, этот процесс подчиняется одной общей закономерности, установленной английским физиком С. Хокингом в 1972 г.: площадь поверхности черной дыры не может уменьшаться со временем (рис. 5). Соответствующая

Рис. 5. Возможные процессы с черными дырами. Иллюстрация к теореме Хокинга. Плоскости t1, t2, t3 обозначают пространственные сечения в соответствующие моменты времени, S0(tl) — площадь черной дыры о в момент времени ti. Две черные дыры могут сливаться в одну, черные дыры могут возникать, площадь поверхности одиночной черной дыры возрастает со временем. Одна черная дыра не может распасться на две или более черных дыр. Теорема Хокинга утверждает, что общая площадь поверхностей черных дыр в момент ( является неубывающей функцией времени

теорема была доказана им при самых широких предположениях, среди которых наиболее существенным является предположение о положительности плотности энергии вещества и физических полей, с которыми взаимодействует черная дыра. Это предположение, безусловно справедливое в рамках классической физики, мо-

жет, однако, нарушаться при учете квантовых эффектов, Доказательство этой теоремы основано на том, что падение в черную дыру вещества и поля, плотность энергии которых положительна, приводит к возрастанию энергии черной дыры, а следовательно, и площади ее поверхности. Для невращающейся незаряженной черной дыры в этом легко убедиться, используя связь между массой М и площадью поверхности А : А = = 16pi(GM/c2)2, Обратный процесс извлечения вещества и энергии из-под горизонта событий невозможен.

Теорема Хокинга справедлива и в более общем случае, когда имеется несколько черных дыр. При их взаимодействии сумма площадей поверхностей черных дыр не уменьшается со временем. Используя эту теорему, удается, в частности, доказать, что одиночная черная дыра не может распасться на две меньшие черные дыры. Для того чтобы убедиться в этом, предположим сначала, что процесс распада черной дыры с массой М, угловым моментом J и зарядом Q возможен, и в результате этого процесса образуются две далеко отстоящие друг от друга черные дыры с массами М1 и М2, угловыми моментами J1 и J2 и зарядами Q1 и q2. В соответствии с .законами сохранения энергии и электрического заряда Q = Q1 + Q2, M>=M1+M2

Неравенство возникает из-за того, что часть энергии при распаде может быть унесена гравитационным, а при наличии заряда — и электромагнитным излучением. Это излучение может унести также полный угловой момент или часть его. Можно убедиться, что эти соотношения противоречат условию возрастания площади поверхности черных дыр: A1+A2>=A.

Обратный процесс слияния двух черных дыр возможен. Этот процесс может сопровождаться излучением гравитационных волн. Если при слиянии черных дыр с массами М1 и М2 образуется дыра с массой М, то уносимая излучением доля энергии epsilon=(M1 + M2—M)/(M1+M2) не превосходит величины 1—2-3/2= 0,64647... Если заряды этих дыр равны нулю или имеют одинаковый знак,