Н.М. Кащенко
1. Численный метод интегрирования вырожденных эллиптических уравнений
В предположении обычных при моделировании ионосферы приближениях малости инерционных сил для заряженной составляющей плазмы и квазипотенциальности силовых линий магнитного поля Земли уравнения переноса заряженных частиц имеют вид [3]:
(1)
В этих уравнениях ni — концентрация частиц, qi — источники и потери, 
— матрица коэффициентов диффузии, имеющая только продольные компоненты, 
— скорость переноса частиц. Аналогичный вид имеют уравнения теплопроводности.
Часто удобно решать уравнения таких моделей конечно-разностным методом на прямоугольных сетках в сферической системе координат. При этом возникает проблема решения вырожденных эллиптических уравнений со смешанными производными. Разностная аппроксимация таких уравнений приводит к разностным схемам, для которых не выполнено условие монотонности даже при аппроксимации в терминах потоков. Запись этих уравнений в дипольной системе координат после аппроксимации по переменной t приводит к уравнениям вида:
(-Au¢ + Bu)¢ + Cu = D, A > 0, C 
0, D 0. (2)
Здесь дифференцирование проводится по продольной координате, которую обозначим b.
Для решения таких уравнений предлагается в (2) факторизовать дифференциальный оператор (дифференциальная прогонка), затем факторизованную запись преобразовать в сферическую систему координат и решать факторизованные уравнения в этой системе по схеме бегущего счета. После факторизации уравнения (2) получаем систему
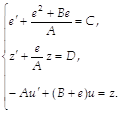(3)
Здесь e и z являются вспомогательными функциями. Первое и второе уравнения интегрируются в направлении возрастания b, а третье интегрируется в направлении убывания b. Систему (3) можно решать на прямоугольной сетке исходной системы координат, используя соответствующие разностные аппроксимации и схемы бегущего счета.
Пусть (x, y) — исходная система координат, а (a, b) — новая система и пусть для формул перехода справедливо соотношение:
Тогда 
поэтому 
и 
аппроксимируются разностями назад при n > 0 и разностями вперед при n < 0, а 
— разностями в обратном порядке. Аналогичные аппроксимации применяются и для производных по переменной y. Тогда суммарная погрешность аппроксимации имеет вид Dz + (ADu)¢ - uDe - eDu, где Dz, Du, De — погрешности аппроксимаций в уравнениях для z, u и e соответственно.
В зависимости от аппроксимации недифференциальных членов системы (3) получается семейство разностных схем с разными величинами суммарной погрешности аппроксимации. Параметры семейства следует подбирать для получения нужного свойства разностной схемы, например, для получения аппроксимации второго порядка. В ионосферных моделях для дополнительного уменьшения погрешностей аппроксимации область интегрирования делится пополам и применяется встречная дифференциальная прогонка с условиями гладкости решения на границе деления [3]. Описанная схема реализована на языке программирования Fortran в рамках численной модели ионосферы.
2. Некоторые варианты скалярной прогонки
Решение трехточечных разностных уравнений методом прогонки основано на неявной факторизации соответствующего разностного оператора. В [2] рассмотрены некоторые варианты решения трехточечных разностных уравнений, но, как указано в [1], анализ вычислительной устойчивости проведен не полностью. В работе [1] показано, что классическая запись прогонки даже при диагональном преобладании имеет погрешность порядка O(n3), и там же приведены примеры, показывающие, что при количестве узлов порядка 300 и использовании обычной точности могут получаться большие погрешности (десятки процентов и более). Там же указаны способы уменьшения этих погрешностей, в частности, с помощью преобразования прогонки к безразностному виду.
Рассмотрим некоторые варианты прогонок без разностей. В этом случае, как указано в [1], погрешности округлений накапливаются со скоростью не более чем O(n2), а при некоторых условиях на коэффициенты — O(n). Приведем несколько вариантов безразностных прогонок.
1. B = 0. Этот случай рассмотрен в [1], а разностная схема для (2) имеет вид:
ai > 0, bi 0, ci > 0, di 0.
В этих уравнениях выполнено условие диагонального преобладания.
Прямой ход прогонки:
При этом 0 < ei < 1.
Обратный ход прогонки:
Здесь 
Следовательно, формулы обратного хода можно записать в безразностном виде:
Кроме уменьшения порядка роста погрешностей этот вариант прогонки доказывает однозначную разрешимость соответствующих разностных уравнений.
2. B ¹ 0. В этом случае разностная схема имеет вид:
ai > 0, bi 0, ci > 0, di 0.
В этих уравнениях условие диагонального преобладания в общем случае не выполнено.
Прямой ход прогонки:
При этом 0 < ei < 1.
Обратный ход прогонки:
Здесь 
Следовательно, формулы обратного хода можно записать в безразностном виде:
Как и в предыдущем случае, кроме уменьшения порядка роста погрешностей этот вариант прогонки доказывает однозначную разрешимость соответствующих разностных уравнений.
3. Циклический случай с B = 0. Разностные уравнения имеют вид:
ai > 0, bi 0, ci > 0, di 0,
Прямой ход прогонки:
Вспомогательный ход прогонки:
Вычисление Yn:
В этих формулах величины ri, si, ui соответствуют уравнениям:
Обратный ход прогонки:
В этом варианте прогонки также отсутствуют разности, что, как и в предыдущих случаях, кроме уменьшения порядка роста погрешностей доказывает однозначную разрешимость соответствующих разностных уравнений.
Список литературы
1. Ильин В.П. Прямой анализ устойчивости метода прогонки // Актуальные проблемы вычислительной математики и математического программирования. Новосибирск: Наука, Сибирское отделение, 1985. С. 189—201
2. Самарский А.А., Николаев Е.С. Методы решения сеточных уравнений. М.: Наука, 1978. 519 с.
3. Кащенко Н.М., Захаров В.Е. Численный метод интегрирования системы уравнений переноса ионосферной плазмы // Доклады международного математического семинара. Калининград: Издательство КГУ, 2002. С. 287—290
Для подготовки данной работы были использованы материалы с сайта http://old.albertina.ru/
0 комментариев