Курсовая работа
по физике
на тему: Анализ зависимости условного периода, логарифмического декремента затухания и добротности контура от его параметров (L,C,R)
Введение
Некоторые значения установки:
С1 = 260 пФ
С2 = 140 пФ
С3 = 230 пФ
С4 = 430 пФ
Логарифмический декремент затухания вычислим по следующей формуле:
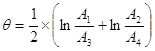 ,
,
где А1, А2, А3 и А4 – значения последовательных амплитуд, определенных по графику.
Задание 1. Проверка зависимости периода колебаний от ёмкости и определения индуктивности катушки
Установим переключатели магазина сопротивлений в нулевое положение.
Установим значение ёмкости С1 и получим на экране устойчивую картину затухающих колебаний.
Измерим логарифмический декремент затухания и проверим выполнение условия ![]() . Если условие выполнено, измерьте период колебаний.
. Если условие выполнено, измерьте период колебаний.
Включим ёмкость С1+ С2 и повторим п.3.
Повторим все измерения для всех возможных ёмкостей. В результате получим набор пар соответствующих значений (Сi, Тi), где i – номер опыта.
Теория предсказывает зависимость между переменными:
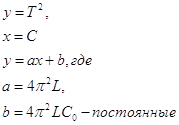
Располагая измеренными значениями Тi при различных Сi вычислим y и по формулам найдём a и b.
Найдём индуктивность.
Найдём паразитную ёмкость С0 .
Вычислим c2
Установим с помощью магазина дополнительное сопротивление контура 1000-3000 Ом.
Повторим пункты 2-11, определяя значение L. Оно отличается от найденного в начале из-за того, что проволочные катушки магазина сопротивления также имеют заметную индуктивность.
| № п/п | Значение емкости контура С | А1 | А2 | А3 | А4 |
| Т |
| 1. | С1 | 20.0 | 13.0 | 10.5 | 6.0 | 0.71 | 12.0 |
| 2. | С1 + С2 | 20.0 | 12.5 | 9.5 | 4.5 | 0.88 | 14.0 |
| 3. | С1 + С3 | 19.5 | 11.5 | 9.0 | 4.5 | 0.85 | 15.5 |
| 4. | С1 + С2 + С3 | 18.5 | 11.0 | 8.0 | 4.0 | 0.92 | 17.0 |
| 5. | С1 + С4 | 18.5 | 10.5 | 8.0 | 3.5 | 0.97 | 18.0 |
| 6. | С1 + С2 + С4 | 18.0 | 9.5 | 7.5 | 3.5 | 0.94 | 19.0 |
| 7. | С1 + С3 + С4 | 18.0 | 9.5 | 7.0 | 3.5 | 0.97 | 19.5 |
| 8. | С1 + С2 + С3 + С4 | 17.0 | 9.0 | 6.5 | 3.0 | 0.98 | 21.0 |
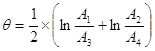 пишешь для каждого случая(1-8)
пишешь для каждого случая(1-8)
y = 0.336´x + 55.55
DА = 0.013 Гн
DВ = 9.21 мкс2
L = 9.3 мГн
DL = 0.3 мГн
С0 = 151.9 пФ
DС0 = 25.8 пФ
c2 = 0.0
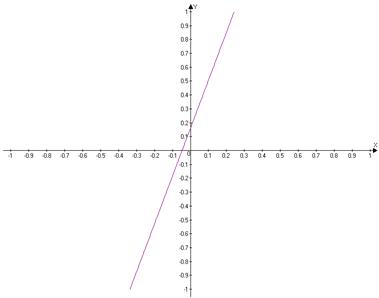
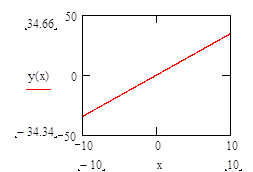
Построим график зависимости y(x).
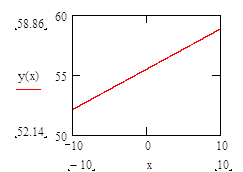
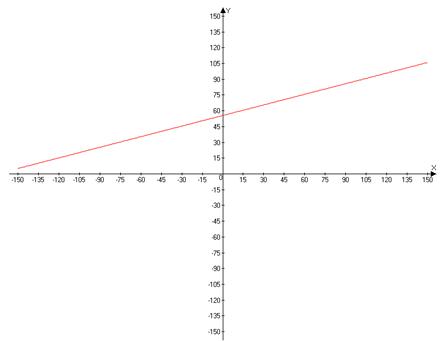
Задание 2. Проверка зависимости логарифмического декремента затухания от сопротивления контура
Установим все переключатели магазина сопротивлений в нулевое положение.
Установим значение ёмкости С1 и получим на экране устойчивую картину затухающих колебаний. Затем измерим период колебаний.
Измерим логарифмический декремент и проверим выполнение условия ![]() .
.
Установим на магазине сопротивлений 300 Ом и повторим измерение периода колебаний и логарифмического декремента, опять проверив условие ![]() .
.
Повторим измерения периода логарифмического декремента при сопротивлении магазина 600 Ом, 900 Ом.
Убедимся в независимости периода колебаний от сопротивления
Теория предсказывает линейную зависимость между величиной сопротивления магазина при постоянном токе (x=R) и логарифмическим декрементом y= ![]() :
:
![]()
Вычислим c2
Найдём сопротивление катушки.
Включим в контур ёмкость С1+ С2 и повторим пункты 1-9.
| № п/п | Значение активного сопротивления R | А1 | А2 | А3 | А4 | T |
| 1. | 300 | 18.0 | 11.0 | 8.5 | 4.0 | 12.0 |
| 2. | 600 | 16.5 | 9.0 | 7.0 | 3.0 | 12.0 |
| 3. | 900 | 15.0 | 8.0 | 5.5 | 2.5 | 12.5 |
| 4. | 1200 | 14.0 | 6.5 | 5.0 | 2.0 | 11.5 |
| 5. | 1500 | 12.5 | 5.5 | 4.0 | 1.5 | 11.5 |
| 6. | 1800 | 11.0 | 4.0 | 3.5 | 1.0 | 11.0 |
| 7. | 2100 | 10.0 | 3.5 | 3.0 | 0.5 | 10.5 |
| 8. | 2400 | 9.0 | 3.0 | 2.5 | 0.5 | 10.3 |
| 9. | 2700 | 8.5 | 2.5 | 2.0 | 0.2 | 10.0 |
| № п/п | Teta | DTeta |
| 1. | 0.8810 | 0.0558 |
| 2. | 0.9780 | 0.0714 |
| 3. | 1.1948 | 0.0909 |
| 4. | 1.2480 | 0.100 |
| 5. | 1.4221 | 0.1250 |
| 6. | 1.6123 | 0.1429 |
| 7. | 1.5749 | 0.1667 |
| 8. | 1.8829 | 0.210 |
| 9. | 1.9040 | 0.2213 |
y = 0.45´x + 0.74 (y – Teta, x – R)
DА = 0.03 1/кОм
DВ = 0.05
c2 = 1.34
Построим график зависимости y(x).
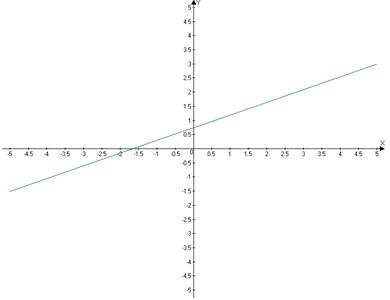
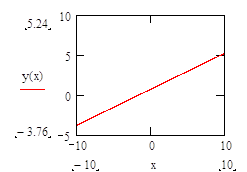
Задание 3. Проверка зависимости сопротивления катушки от периода колебаний
Установим в магазине сопротивлений все переключатели в нулевое положение.
Установим значение ёмкости С1 получим на экране устойчивую картину затухающих колебаний и измерим период Т и логарифмический декремент ![]() .
.
По формуле
![]()
вычислим сопротивление катушки.
Повторим измерения и вычисления сопротивления катушки при всех возможных значениях ёмкости контура.
На координатной плоскости по оси x откладываем значения
![]() ,
,
а по оси y – R.
Убедимся в линейной зависимости между x и y.
| № п/п | Значение емкости контура С | А1 | А2 | А3 | А4 |
| Т | R |
| 1. | С1 | 20.0 | 13.0 | 10.5 | 6.0 | 0.71 | 12.0 | 1.100 |
| 2. | С1 + С2 | 20.0 | 12.5 | 9.5 | 4.5 | 0.88 | 14.0 | 1.169 |
| 3. | С1 + С3 | 19.5 | 11.5 | 9.0 | 4.5 | 0.85 | 15.5 | 1.020 |
| 4. | С1 + С2 + С3 | 18.5 | 11.0 | 8.0 | 4.0 | 0.92 | 17.0 | 1.006 |
| 5. | С1 + С4 | 18.5 | 10.5 | 8.0 | 3.5 | 0.97 | 18.0 | 1.002 |
| 6. | С1 + С2 + С4 | 18.0 | 9.5 | 7.5 | 3.5 | 0.94 | 19.0 | 0.920 |
| 7. | С1 + С3 + С4 | 18.0 | 9.5 | 7.0 | 3.5 | 0.97 | 19.5 | 0.925 |
| 8. | С1 + С2 + С3 + С4 | 17.0 | 9.0 | 6.5 | 3.0 | 0.98 | 21.0 | 1.089 |
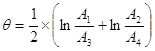
пишешь для каждого случая(1-8),потом расписываешь R
Значения сопротивлений найдем с помощью формулы:
![]()
| № п/п | Teta | DTeta |
| 1. | 0.709 | 0.048 |
| 2. | 0.833 | 0.053 |
| 3. | 0.856 | 0.056 |
| 4. | 0.925 | 0.063 |
| 5. | 0.968 | 0.063 |
| 6. | 0.937 | 0.067 |
| 7. | 0.971 | 0.071 |
| 8. | 1.030 | 0.077 |
y = 3.45´x + 0.16 (y – R)
DА = 0.744 Ом´мкс½
DВ = 0.191 Ом
c2 = 1.50
Построим график зависимости y(x).
Похожие работы
... для графа на рис. 3, приняв, что дерево образовано ветвями 2, 1 и 5 Ответ: B= Решить задачу 5, используя соотношения (8) и (9). Теория / ТОЭ / Лекция N 3. Представление синусоидальных величин с помощью векторов и комплексных чисел. Переменный ток долгое время не находил практического ...
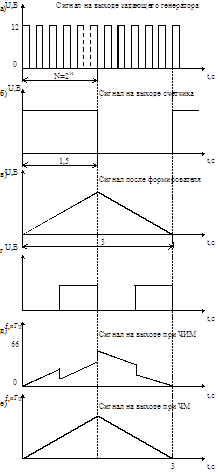
... К50-35 должен быть рассчитан на напряжение не менее 16 В. Также будут применены конденсаторы К10-17. Погрешность их должна быть не больше ±20%. В физиотерапевтическом устройстве на основе применения упругих волн применен повышающий трансформатор. Работает он на частотах до 66000 Гц. В связи с этим в трансформаторе необходимо использовать торроидальный сердечник. Это уменьшит габариты изделия. Для ...
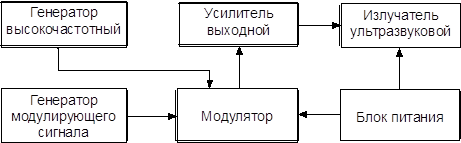
0 комментариев