МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Инженерно физическое отделение
Кафедра физики твердого тела
АНОМАЛЬНОЕ ТЕМПЕРАТУРНОЕ ПОВЕДЕНИЕ МАГНИТНОГО КРУГОВОГО ДИХРОИЗМА В ОКСИДНОМ СТЕКЛЕ С ДИСПРОЗИЕМ
Красноярск 2009
Оглавление
Введение
Описание измерительных установок и методов измерения
Результаты измерений и их обсуждение
Заключение
Литература
Введение
В настоящее время часто для исследования энергетической и кристаллохимической структуры твердого тела привлекают методы исследования во внешних полях. Среди них особое место занимают методы исследования в магнитном поле. Специфика этих методов состоит в том, что влияние магнитного поля на систему не может быть описано заданием обычного вектора напряженности поля, как это имеет место в случае электрического поля. В результате, помимо обычной оптической анизотропии, которая всегда возникает в среде под влиянием внешних полей и деформаций, в магнитном поле возникает дополнительная, циркулярная анизотропия, связанная с неэквивалентностью двух направлений вращения в плоскости, перпендикулярной полю.
В анизотропных кристаллах при произвольном направлении волнового вектора магнитное поле влияет на распространение света довольно слабо, вызывая лишь появление слабой дополнительной эллиптичности колебаний. Таким образом, измерения имеет смысл проводить только в направлении оптических осей, где наблюдается своеобразное вырождение – двум поляризациям соответствует одни и те же показатель преломления n и коэффициент поглощения k. В связи с этим особый интерес представляет исследование магнитооптических явлений в оптически изотропных кристаллах кубической группы, где отсутствуют эффекты, связанные с собственной анизотропиeй кристалла, и явления могут наблюдаться в чистом виде. Внешнее магнитное поле снимает в этом случае вырождение двух состояний круговой поляризации для каждого направления распространения, и величины n и k становятся различными для право и левополяризованного света. Это приводит к ряду магнитооптических явлений, тесно связанных между собой.
Магнитооптические явления наблюдаются, как правило, в двух схемах эксперимента: когда вектор световой волны K параллелен магнитному полю H и когда перпендикулярен.
В первом случае могут наблюдаться либо различие в показателях преломления двух циркулярно поляризованных компонент, проявляющееся в повороте плоскости поляризации линейно поляризованного света, – магнитооптическое вращение или эффект Фарадея, либо различие в коэффициентах поглощения для этих компонент – магнитный круговой дихроизм.
В отличие от эффекта Зеемана, исследование которого требует наличия узких спектральных линий, необходимых для разрешения компонент магнитного расщепления в применяемых полях, МКД могут наблюдаться в области широких полос поглощения, характерных для многих систем. Изучение МКД в области полос поглощения позволяет получать качественную и количественную информацию как об основном так и о возбужденных состояниях системы – величинах магнитного расщепления, уровней и симметрии состояний, участвующих в оптических переходах. Кроме того, он позволяет определить локальную симметрию отдельных поглощающих центров системы и тем самым получать жесткий экспериментальный критерий правильности той или иной модели центра.
Наложение магнитного поля снимает все остаточные вырождения энергетических уровней, что придает магнитооптическим исследованиям дополнительную информативность по сравнению с иными методами исследования во внешних полях.
Стекла, активированные редкоземельными элементами, привлекают внимание исследователей несколько последних десятилетий. Такие стёкла широко используются в качестве материалов для оптических квантовых генераторов и усилителей. В частности, это относится и к стёклам, содержащим ионы Dy3+. Спектры поглощения РЗ ионов в стекольных матрицах исследовались в огромном количестве работ, в том числе, стёкла различных составов, содержащие диспрозий, исследовались, например, в. Магнитный круговой дихроизм, наблюдаемый только в пределах полос поглощения, представляет дополнительные возможности изучения вырожденных электронных уровней, расщепляемых кристаллическим полем, а также и уровней, не разрешаемых в оптических спектрах поглощения. Известны работы, посвященные спектральным зависимостям МКД f-f переходов для Er3+, Pr3+ и Ho3+ в натриевых стеклах, Er3+ в фосфатных стеклах, Ho3+, Nd3+ и Pr3+ во фторидно-цирконатных стеклах. В впервые были представлены спектры МКД Dy3+ в оксидных стеклах совместно со спектрами поглощения для ряда f-f переходов и обнаружено существенное различие парамагнитной магнитооптической активности этих переходов. Для выяснения природы этого явления в настоящей работе предпринято исследование температурной зависимости МОА f-f перехода 6H15/2→ 6 в Dy3+ в алюмо-боро-силико-германатном оксидном стекле.
Описание измерительных установок и метода измерения
Спектры поглощения получены по двухлучевой методике на автоматическом спектрометре, сконструированном на базе монохроматора МДР‑2.
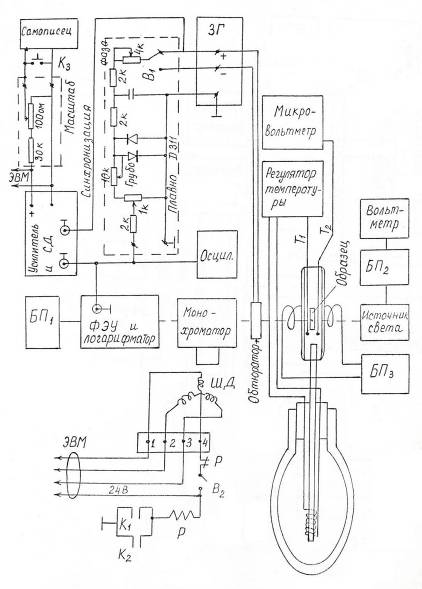
Схема установки
Спектрометр предназначен для получения спектров поглощения. Спектральный диапазон измерений от 2000 до 11000 Å. Максимальное разрешение 20 см-1. Динамический диапазон измеряемой оптической плотности от 0 до 3. Световой поток от источника света конденсором направляется на образец. Затем изображение образца с помощью линзы фокусируется на верхнюю половинку щели монохроматора. Перед щелью расположен обтюратор, колеблющийся с частотой напряжения, подаваемого от звукового генератора ЗГ. Колеблющийся обтюратор попеременно открывает верхнюю и нижнюю части щели монохроматора. Световой поток, прошедший через образец, попадает на верхнюю половину щели. Его интенсивность:
I=I0·10-αl
где I0 – интенсивность светового потока, прошедшего через нижнюю часть щели монохроматора мимо образца; α – коэффициент поглощения образца, l – толщина образца.
Из монохроматора световые потоки I0 и I попадают в фотоэлектронный умножитель, который преобразует их в фототоки. Логарифмический усилитель преобразует фототоки в напряжения, пропорциональные логарифмам потоков I0 и I. В результате переменное напряжение на выходе логарифматора:
ΔU ~ l g I 0 – l g I = l g = α l
оказывается пропорциональным коэффициенту поглощения образца и его оптической плотности.
Устройство спектрометра
Источником света служит лампа КГМ 12x100. Подаваемое на лампу напряжение контролируется вольтметром. Ширины щелей монохроматора ДМР‑4 регулируются встроенными микрометрическими винтами. Монохроматор имеет также насадку, которая делит входную щель на два открытых участка по вертикали. Размеры их могут плавно изменяться. Перед щелью монохроматора может помещаться светофильтр. На барабане монохроматора нанесена шкала от 0 до 350 делений, которая составляет один поддиапазон. Барабан приводится в движение шаговым двигателем или синхронным двигателем. Диапазон измерений монохроматора разбит на четыре поддиапазона. По специальной таблице можно перевести каждую шкалу в Å или см-1.
Фотоприемником служит ФЭУ‑62, синхронизированный звуковым генератором ЗГ. Для смещения начала отсчета коэффициента поглощения блок имитатора создает сигнал, аналогичный сигналу от логарифматора. Напряжение с выхода логарифматора регистрируется либо на самописце, либо в АЦП ЭВМ.
Важным преимуществом данного спектрометра является то, что благодаря усилению можно исследовать очень слабые линии поглощения, которые не регистрируются обычным способом.
Блок включает в себя две термопары Т1 и Т2. С помощью регулятора ПИТ‑3 и термопары Т1 осуществляется регулирование температуры в криостате. С помощью термопары Т2, соединенной с микровольтметром, осуществляется контроль температуры.
К ПИТ‑3 подключена печка, которая находится в дюаре с азотом. Регулятор температуры ПИТ‑3 изменяет напряжение на печке и тем самым скорость испарения азота таким образом, чтобы поддерживать ЭДС термопары Т1 постоянной и равной величине, установленной на передней панели ПИТ‑3
Описание установки для измерения МКД
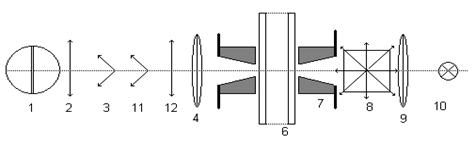
Рис. 1. Оптическая схема измерения
1 – входная щель монохроматора
2 – поляризатор
3 – пьезомодулятор
4 – линза
5 – образец
6 – проточный криостат
7 – электромагнит
8 – деполяризатор
9 – конденсор
10 – источник света
11 – регулируемая фазовая пластинка
12 – поляризатор
Принцип действия
Плоскость поляризации поляризатора 2 выставляется под углом 45 град. к главным осям модулятора 3. Для этого перед модулятором ставится дополнительный поляризатор 12 в положение наименьшего пропускания света при выключенном модуляторе. Затем, при включённом модуляторе, вращением поляризаторов 2 и 12 снова находится положение наименьшего пропускания света. При этом поляризации поляризаторов будут параллельны к главным осям модулятора. Теперь поляризатор 2 поворачивают на 45 град. Ориентация жёстко связанного комплекса модулятор 3 – поляризатор 2 относительно входной щели монохроматора 1 в принципе не важна, но стоит установить её так, чтобы реакция ФЭУ к постоянному световому потоку при убранном поляризаторе 12 была максимальна.
Конденсор 9 концентрирует свет на образце. Для измерений наилучшим является параллельный пучок, но тогда мала освещённость образца и велики шумы при измерении. Приходится выбирать оптимум. Линза 4 фокусирует изображение образца на входную щель 1. Пара элементов – поляризатор 2 и модулятор 3 устанавливают пропускание света, поляризованного направо или налево, так что модулируется световой поток в соответствии с круговым дихроизмом образца.
Результаты измерений и их обсуждение
В предлагаемой работе исследованы температурные зависимости спектров поглощения и магнитного кругового дихроизма f-f перехода 6H15/2→ 6 в ионе Dy3+ в оксидном стекле: Dy2O3-La2O3-Al2O3-B2O3-SiO2-GeO2, где массовая концентрация Dy2O3 составляет 43.3%. Спектр поглощения стекла в инфракрасной области при комнатной температуре показан на рис. 1.
Магнитооптические свойства переходов в состояния 6F5/2 и 6 были изучены ранее. На основании температурных зависимостей спектров поглощения и МКД получена температурная зависимость интегральной парамагнитной магнитооптической активности перехода, представленная на рис. 3.
Ван Флек и Хебб показали, что парамагнитная МОА пропорциональна парамагнитной восприимчивости: a=Kχ. Однако коэффициент пропорциональности K зависит не только от типа иона и длины волны наблюдения, но и от свойства электронного перехода, ответственного за наблюдаемый магнитооптический эффект. Эксперименты подтверждают, что температурные зависимости этих величин действительно совпадают, когда измеряется эффект Фарадея, обусловленный сильными переходами, т.е., МОА возрастает по абсолютной величине при понижении температуры и подчиняется закону Кюри или Кюри-Вейсса. Подчиняется закону Кюри-Вейсса и МОА f-f переходов в том же стекле, которые были изучены в. Однако полученный в данной работе результат показывает, что в случае запрещённых по чётности f-f переходов возможно существенное различие температурных зависимостей МОА и парамагнитной восприимчивости.
Интегральная парамагнитная МОА перехода между J‑мультиплетами, когда она подчиняется закону Кюри, может быть записана в виде:
Здесь k и Δk – коэффициент поглощения и МКД, соответственно, относящиеся к полосе поглощения J1 → J2, H – магнитное поле, T – температура, A – константа, характеризующая МОА конкретного перехода. Как интенсивность, так и МОА запрещённых по чётности f-f переходов обязаны разрешённым переходам между состояниями противоположной чётности, которые примешиваются к 4f состояниям нецентросимметричной компонентой кристаллического поля, как статического, так и связанного с колебаниями решётки. Парамагнитная МОА разрешённых переходов между J мультиплетами равна:
для перехода J →: A = – g / 2,
для перехода J → J: A = – g/2,
для перехода J →: A = + g J / 2,
где g – фактор Ланде исходного состояния. Для разрешённых переходов МОА, описываемые соотношениями, вполне однозначны. Для f-f переходов эти величины дают только максимально возможные МОА, так как, прежде всего, несколько примесей к 4f состояниям может иметь место. Кроме того, имеются существенные различия между магнитооптическими свойствами ионов с целыми и полуцелыми полными моментами. Ион Dy3+ имеет полуцелый момент. Состояния с полуцелыми моментами, по крайней мере, дважды вырождены в любом КП и имеют магнитный момент. Следовательно, зависящий от температуры МКД должен существовать.
Состояния, примешанные к 4f состояниям, должны также обеспечивать разрешение по полному моменту согласно правилу отбора: 
, где Ji – полный момент исходного состояния, а 
- примеси к конечному состоянию. Таким образом, разрешение f-f переходов из основного состояния J=15/2 может быть обеспечено примесью состояний с J=13/2, J=15/2 и J=17/2 к возбуждённому 4f состоянию. С помощью находим, что МОА переходов в упомянутые состояния: A= -5.66, -0.66 и +5, соответственно, при g=4/3. Из экспериментальных данных при T=293 K, когда наиболее равномерно заселены компоненты расщепления основного состояния в КП, находим: Aexp= -0.78. Сравнивая эту величину с теоретически возможными, приходим к выводу, что в разрешении перехода могут принимать участие одновременно все перечисленные выше примеси к возбуждённому состоянию.
Заключение
Таким образом, парамагнитная МОА исследованного f-f перехода состоит из нескольких вкладов различной величины и знака. Соотношение вкладов зависит от заселенности компонент расщепления основного состояния кристаллическим полем, что приводит к дополнительной зависимости интегральной МОА от температуры, которая в данном веществе и для данного перехода оказывается принципиально отличной от закона Кюри-Вейсса.
Литература
1. S. Tanabe. J. Non-Cryst. Solids 259, 1.
2. Y. Guimond, J.L. Adam, A.M. Jurdyc, J. Mugnier, B. Jacquier, X.H. Zhang. Optical Materials 12, 467.
3. I.S. Edelman, A.V. Malakhovskii, A.M. Potseluyko, T.V. Zarubina, A.V. Zamkov. J. Non-Cryst. Solids 306, 120.
4. K. Binnemans, R. Van Deun, C. Görller-Walrand, J.L. Adam. J. Non-Cryst. Solids 238, 11.
5. P. Babu, C.K. Jayasankar. Optical materials 15, 65.
6. M. Jayasimhadri, D.V.R. Moorthy, R.V.S.S.N. Ravi Kumar. J. Alloys and Comp. 408–412, 724.
7. S.J. Collocott and K.N.R. Taylor. J. Phys. C: Solid State Phys. 11, 2885.
8. S.J. Collocott and K.N.R. Taylor. J. Phys. C: Solid State Phys. 12 1767.
9. U.V. Valiev, A.A. Klochkov, A.S. Moskvin and P. Shiroki. Opt. Spectrosc. 69, 68.
10. A.A. Klochkov, U.V. Valiev and A.S. Moskvin. Phys. Stat. Sol. 167, 337.
11. K. Binnemans, C. Gorller-Walrand, J. Lucas, N. Duhamel and J.L. Adam. J. Alloys Compounds 225, 80.
12. K. Binnemans, D. Verboven, C. Gorller-Walrand, J. Lucas, N. Duhamel and J.L. Adam. J. Non-Cryst. Solids 204, 178.
13. K. Binnemans, D. Verboven, C. Gorller-Walrand, J. Lucas, N. Duhamel-Henry, J.L. Adam. J. Alloys Compounds 250, 321.
14. В.А. Исаченко, А.Л. Сухачев. Вестник КрасГУ 4, 68.
15. J.H. Van Vleck, M.H. Hebb, Phys. Rev., 1934.-V.46. – P.17.
16. А.В. Малаховский, В.А. Исаченко, А.Л. Сухачев, А.М. Поцелуйко, В.Н. Заблуда, Т.В. Зарубина, И.С. Эдельман.ФТТ, 2007.-Т.49. – №4.-С. 667.
0 комментариев