Взаимодействия двух радикально пульсирующих пузырьков газа в жидкости

МИНЕСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

РОССИЙСКОЙ ФЕДЕРАЦИИ

ТАТАРСКИЙ ГОСУДАРСТВЕННЫЙ ГУМАНИТАРНО-ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ

Математический факультет

Кафедра вычислительной математики, информатики и методики ее преподавания

КУРСОВАЯ РАБОТА

взаимодействия двух радиально пульсирующих пузырьков газа в жидкости

Выполнил студент 146 группы: Вафин А.А.

Научный руководитель: д. ф. – м. н. Аганин А. А.

Казань – 2007

Содержание Введение 1.         Постановка задачи в рамках уравнений динамики жидкости 2.         Математическая модель взаимодействия пузырьков 3.         Методика решения 4.         Исследование взаимодействия двух радиально пульсирующих пузырьков газа в жидкости 5.         Заключение 6.         Литература 7.         Приложение. (Программа расчета).
Введение

К настоящему времени довольно хорошо изучена динамика отдельного пузырька газа в жидкости. Полученные в этом отношении результаты имеют важное теоретическое и прикладное значение. Вместе с тем, в реальных жидкостях, как правило, присутствует не один, а множество пузырьков, так что свойства жидкостей существенно зависят от особенностей взаимодействия между пузырьками. В силу большей сложности этот вопрос является менее изученным, хотя он и имеет важное прикладное значение.

В данной курсовой работе исследуется взаимодействия двух радиально пульсирующих пузырьков газа в жидкости ранние выведенной математической модели. В принципе, такое взаимодействие можно изучать и на основе широко известных уравнений Навье-Стокса методом прямого численного моделирования. Однако такой подход пока не используется в силу больших потребностей компьютерного времени даже на современных компьютерах с высоким быстродействием. В модели, использующейся в курсовой работе, жидкость считается невязкой несжимаемой, пузырьки – осесимметричными. Пузырьки расположены сносно. Их общая ось симметрии направлена вертикально вдоль действия силы тяжести. Пузырьки совершают нелинейные радиальные колебания, а скорости их вертикального пространственного перемещения считаются малыми. Используются три системы отсчета, одна неподвижная и две подвижные. В качестве неподвижной системы приняты декартовые координаты, а в качестве подвижных систем – сферические координаты. Начало отсчета радиальных координат в подвижных сферических системах отсчета связано с центрами пузырьков. Поверхности каждого из пузырьков представляются в виде ряда по поверхностным сферическим гармоникам нулевой, второй, третьей, четвертой и т.д. степеней. При этом сферическая гармоника нулевой степени описывает радиальную составляющую поверхности пузырька, а гармоники второй, третьей и т.д. степеней – отклонения от сферической формы в виде соответствующей гармоники (второй степени – эллипсоидальные отклонения, третьей – грушеобразные и т.д.).

Созданная математическая модель представляет собой систему обыкновенных дифференциальных уравнений второго порядка относительно радиусов пузырьков, пространственного положения их центров и амплитуды отклонений от сферической формы пузырьков в виде сферических поверхностных гармоник. При выводе этих уравнений используются частные решения уравнения Лапласа в сферической системе координат и интеграл Коши-Лагранжа.

Постановка задачи в рамках уравнений динамики жидкости

Рассматривается динамика двух газовых пузырьков в неограниченном объеме невязкой несжимаемой жидкости. Динамика жидкости описывается уравнениями

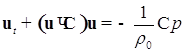, . (1)

Здесь – время эйлеровых (неподвижных) систем координат , ,  (нижний индекс  означает частную производную), – вектор скорости, – плотность жидкости, – давление, , , , –направляющие векторы пространственных координат. Здесь и далее, если не оговорено противное, по повторяющимся индексам предполагается суммирование (здесь от 1 до 3).

Пузырьки расположены вдоль вертикальной оси  неподвижной декартовой системы координат  (рис.1).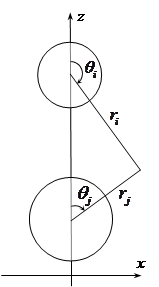

На поверхности каждого пузырька выполняются следующие условия:

кинематическое

, (2)

и динамическое

. (3)

Здесь – скорость точки поверхности пузырька, – нормаль к поверхности пузырька, верхние знаки указывают на отношение к внешней (+) и внутренней (–) сторонам поверхности.

Газ в пузырьках принимается гомобарическим (с однородным распределением давления) с давлением, изменяющимся по закону (Ван-дер-Ваальса)

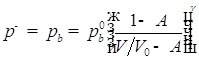, (4)

где – начальное давление газа в пузырьке, – текущий и начальный объемы пузырька, – постоянная, – показатель адиабаты.

На бесконечном удалении от пузырьков давление жидкости  совершает гармонические колебания

, (5)

где – статическое давление в жидкости, , – амплитуда и частота колебаний.

Рассматриваются случай, когда форма пузырьков в интересующем промежутке времени остается относительно близкой к сферической.

 

Математическая модель взаимодействия пузырьков

В пятом приближении относительно  уравнения динамики двух газовых пузырьков в вязкой сжимаемой жидкости представляют собой систему, состоящую из четырех дифференциальных уравнений относительно радиусов пузырьков , координат их центров

;

;

;

;

 

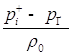
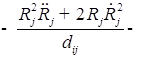
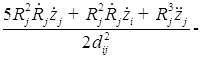
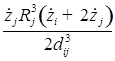
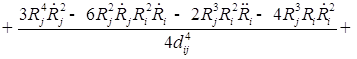
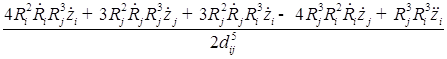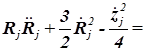
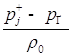
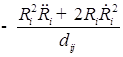
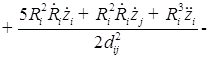
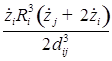
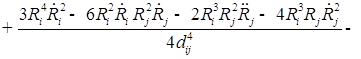
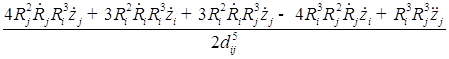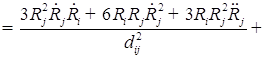
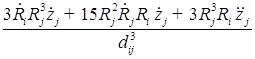
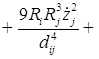
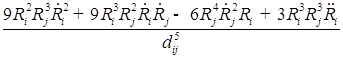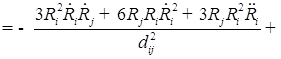
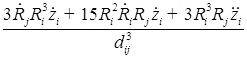
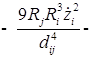
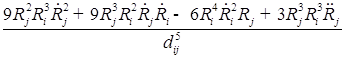Методика решения

Имея четыре уравнения второго порядка относительно радиуса и положения центра пузырьков. Вводим замену, чтобы избавится от второго порядка, и запишем уравнения 1 ого порядка:

Получаем систему 8-и уравнений 1-го порядка относительно радиуса, положения центра пузырьков, скорость изменения радиусов и положения центра пузырьков.

;

()/;

/;

/;

/;

/;

/;

;

()/;

()/;

()/;

/;

/;

()/;

;

/;

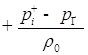
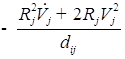
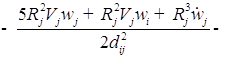
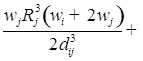
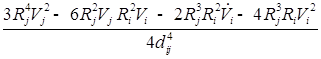
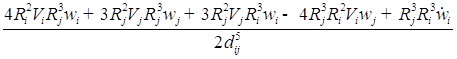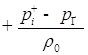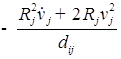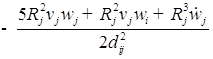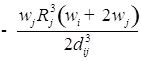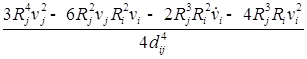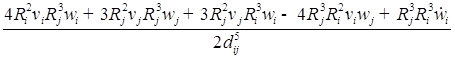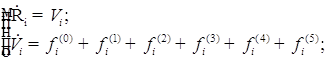
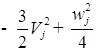
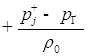
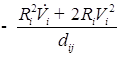
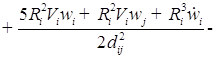
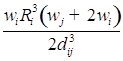
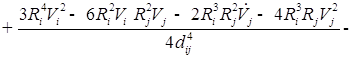
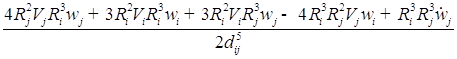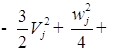
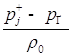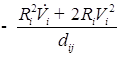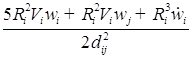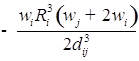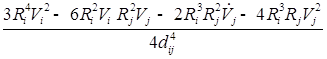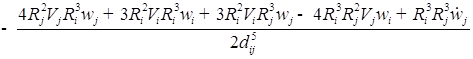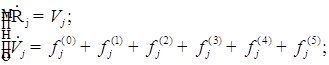
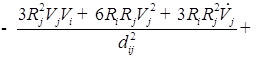
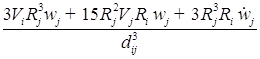
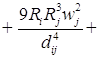
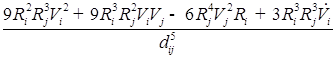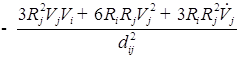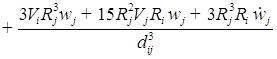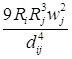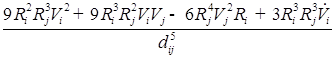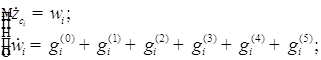
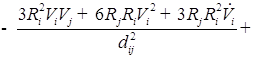
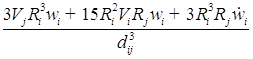
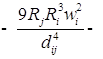
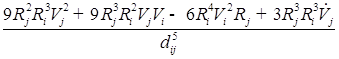0;

()/;

()/;

/;

()/;

;

/;

0;

()/;

()/;

/;

()/;

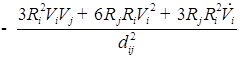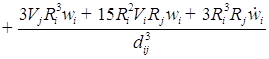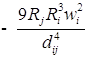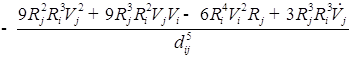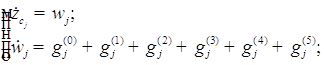
Отсюда получаем данные уравнения в следующем виде:

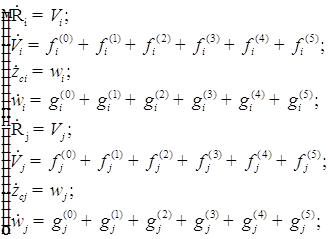
Решим уравнение методом последовательных приближений.

В нулевом приближении данные уравнения записываются относительно радиуса и положения центра пузырьков.

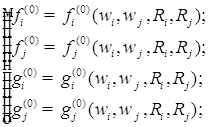
Подставляя выражения, находим уравнения нулевого приближения:

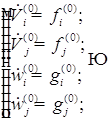
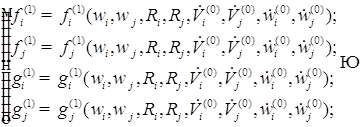
В первом приближении уравнения записываются относительно радиуса, положения центра пузырьков, скорость изменения радиусов и положения центра пузырьков. Полученное первое приближение добавляем к нулевому приближению. И так находим до пятого приближения.

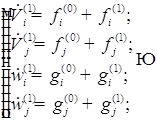
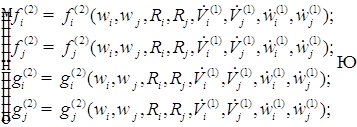
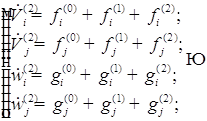
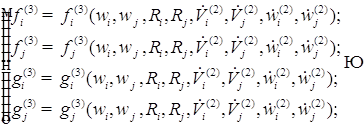
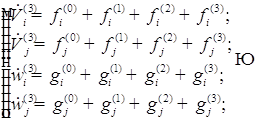
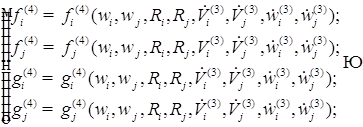
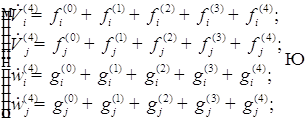
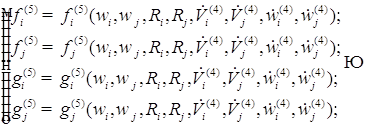
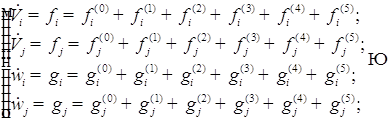
Исходя из этого, можем записать следующую систему:

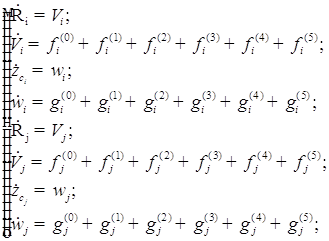
Полученные дифференциальные уравнения решаются методом Дортсмана–Принса восьмой степени точности. (Программа приведена ниже).

 

Исследование взаимодействия двух радиально пульсирующих пузырьков газа в жидкости

Для учета влияния вязкости и сжимаемости жидкости проводим следующую модификацию математической модели. (По аналогии с работой Дойникова[?]).

1.         С учетом сжимаемости жидкости получим следующие уравнения:

;

;

Решение для нулевого приближения для одного пузырька

;

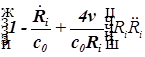
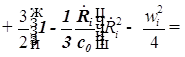
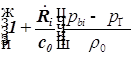
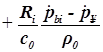
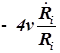
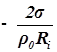
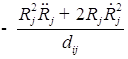
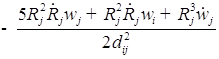
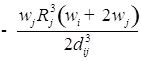
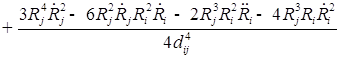
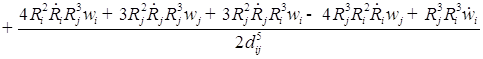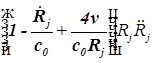
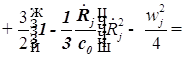
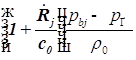
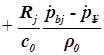
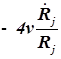
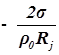
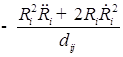
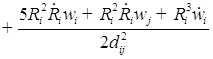
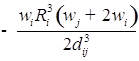
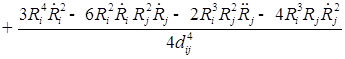
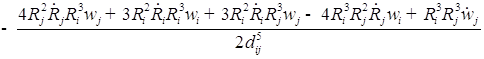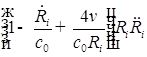
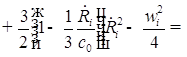
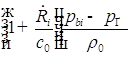
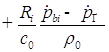
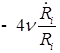
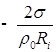Вводим замены:

; ; ;;

= =;

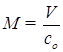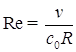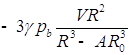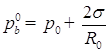- начальное давление газа в пузырьке;

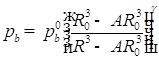 ; -давление газа в пузырьке.

 

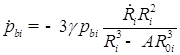
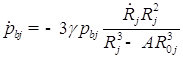
А - константа Ван-дер-Ваальса;

- коэффициент поверхностного натяжения;

 - давление газа в пузырьке;

 - статическое давление в жидкости;

- Начальный радиус пузырька;

R - Радиус пузырька;

 - Центр пузырька;

u - Вектор скорости жидкости;

 

-давление в жидкости на большом удалении от пузырька, где

- амплитуда и частота колебаний давления. Рассматривается лишь один период колебаний ().

- Плотность жидкости;

- Скорость звука в жидкости;

- Кинематический коэффициент вязкости

 - расстояние между пузырьками.

;

;

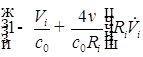
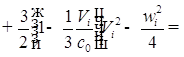
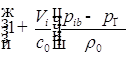
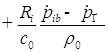
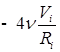
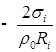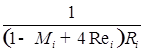
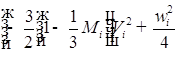
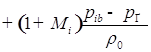
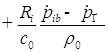
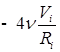
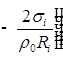Обозначим слагаемые и сомножители через: , ,,,:

; ; ;

; ;

 ;

  ;

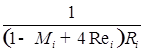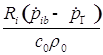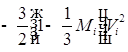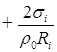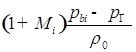Добавляем второе уравнение: =0 =>

;

;

Добавляем уравнение второго пузырька

;

; ; ; = =;

;

;

; ; ;

; ;

;

;

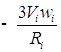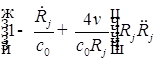
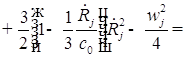
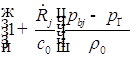
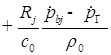
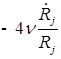
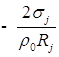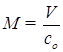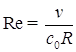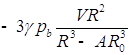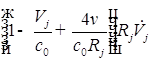
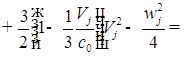
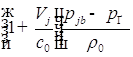
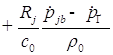
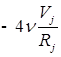
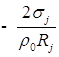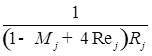
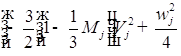
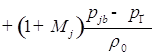
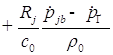
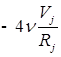
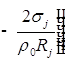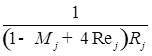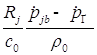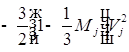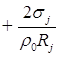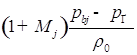Добавляем второе уравнение: =0 =>

;

;

Решение для первого приближения одного пузырька

;

;

;

;

();

;

Добавляем уравнение второго пузырька

;

;

;

;

;

Решение для второго приближения одного пузырька

;

/

;

;

();

;

;

 

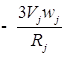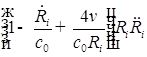
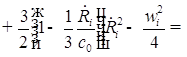
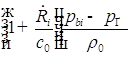
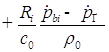
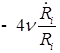
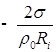
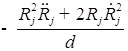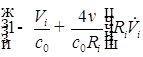
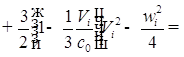
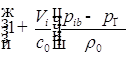
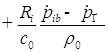
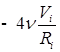
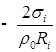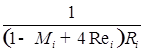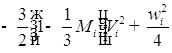
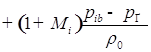
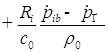
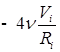
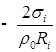
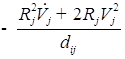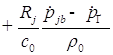
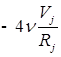
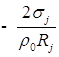
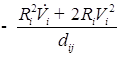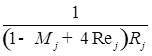
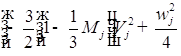
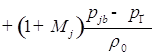
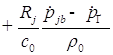
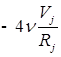
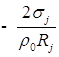
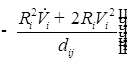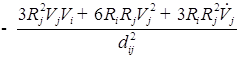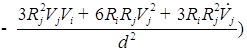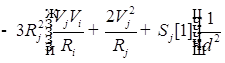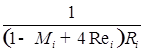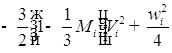
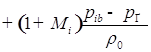
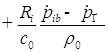
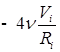
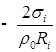
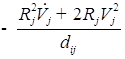
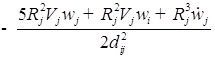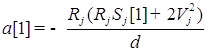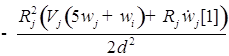Добавляем уравнение второго пузырька

;

;

;

;

;

;

 

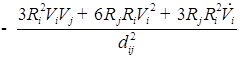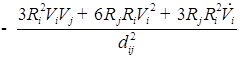
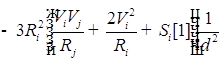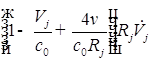
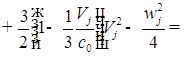
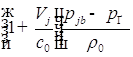
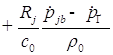
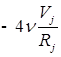
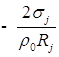
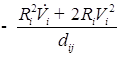
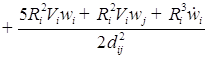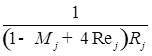
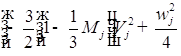
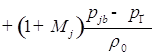
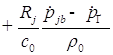
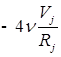
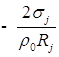
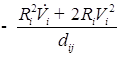
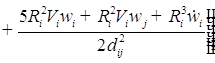Решение для третьего приближения одного пузырька

;

)/

;

;

;

;

;

;

;

 

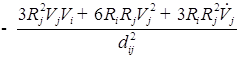
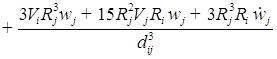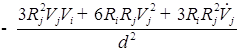
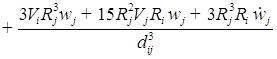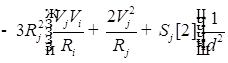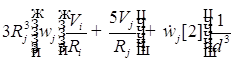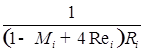
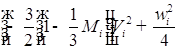
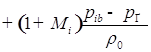
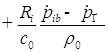
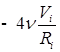
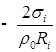
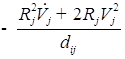
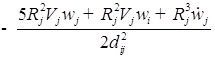
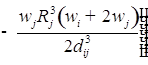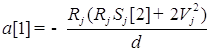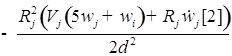Добавляем уравнение второго пузырька

;

;

;

;

;

;

;

;

Решение для четвертого приближения одного пузырька

;

)/

;

;

;

;

;

;

;

;

;

Добавляем уравнение второго пузырька

;

;

;

;

;

;

;

;

;

;

Решение для пятого приближения одного пузырька

;

)/

;

;

;

;

;

;

;

;

;

;

;

 

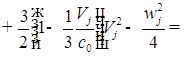
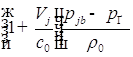
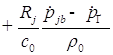
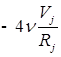
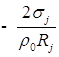
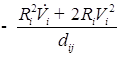
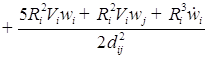
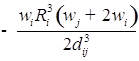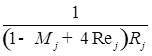
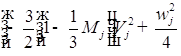
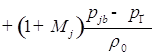
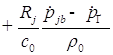
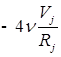
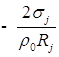
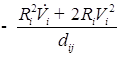
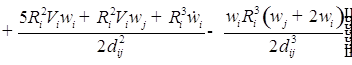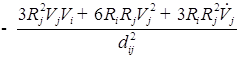
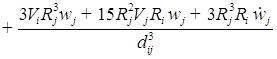
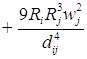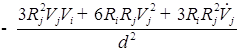
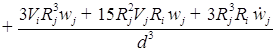
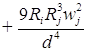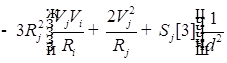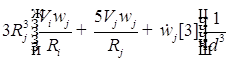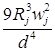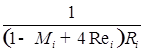
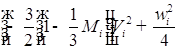
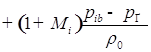
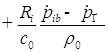
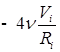
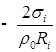
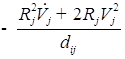
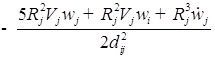
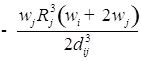
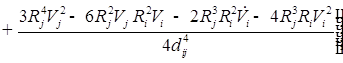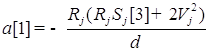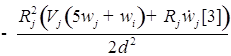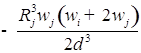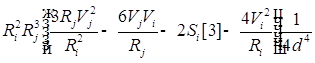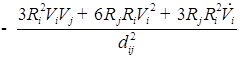
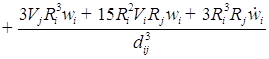
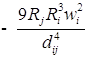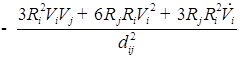
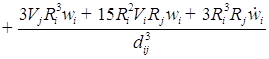
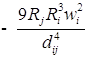
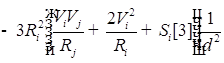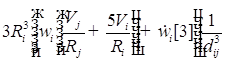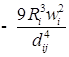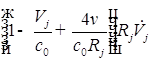
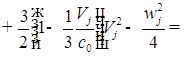
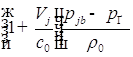
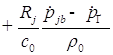
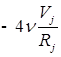
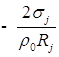
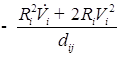
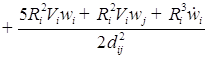
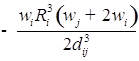
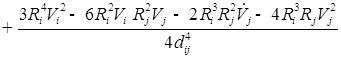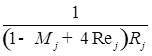
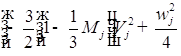
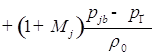
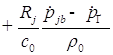
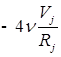
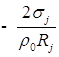
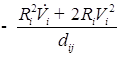
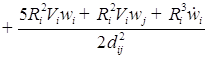
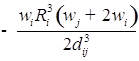
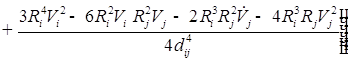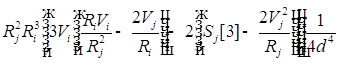
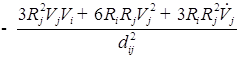
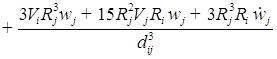
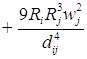
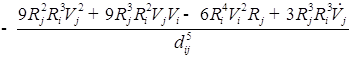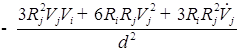
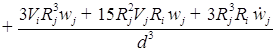
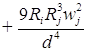
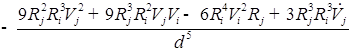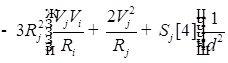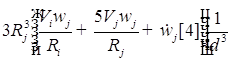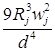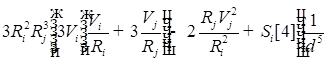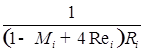
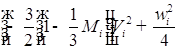
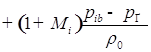
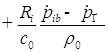
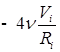
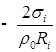
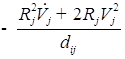
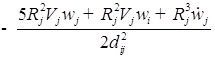
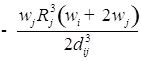
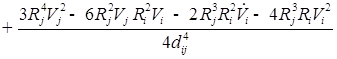
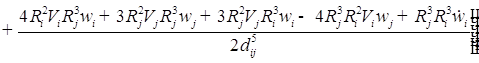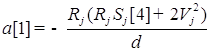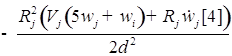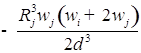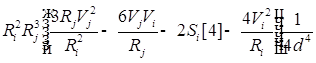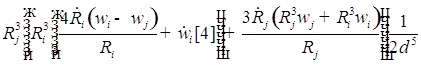Добавляем уравнение второго пузырька

;

;

;

;

;

;

;

;

;

;

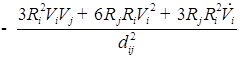
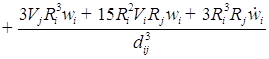
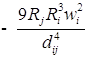
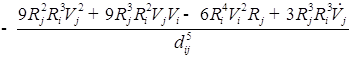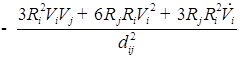
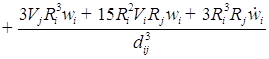
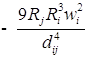
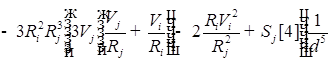
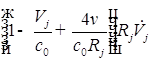
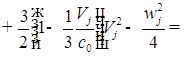
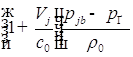
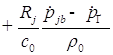
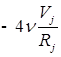
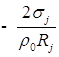
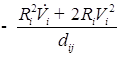
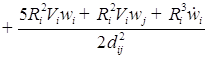
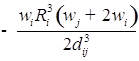
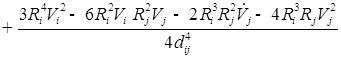
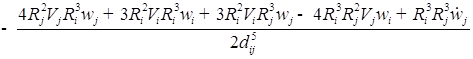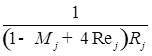
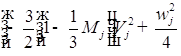
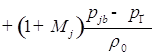
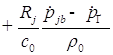
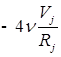
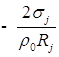
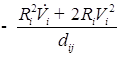
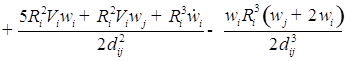
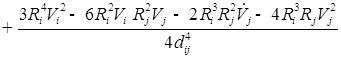
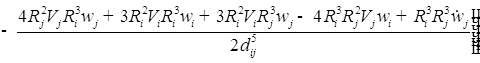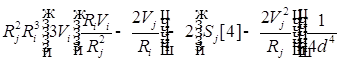
2.         Для исследования добавляем вязкость и решаем уравнение:

;

;

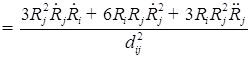
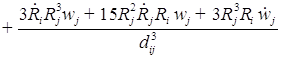
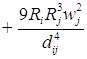
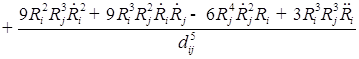
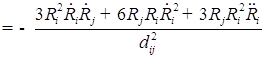
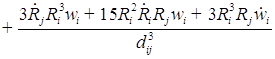
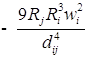
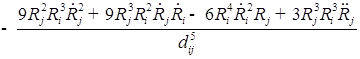
где , (j = 1, i = 2);

 - Кинематический коэффициент вязкости;

,

, , ,

Вводим замену, чтобы избавится от второго порядка, и запишем уравнения 1 ого порядка:

 

Для первого уравнения:

;

=;

;

;

;

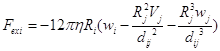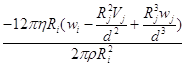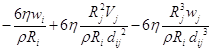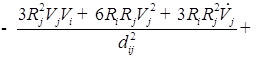
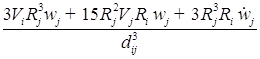
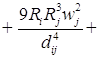
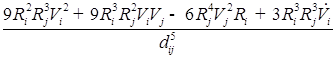
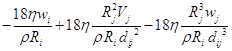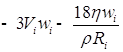
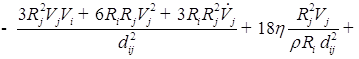
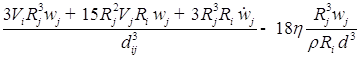
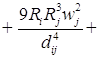
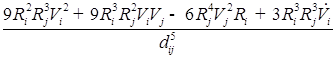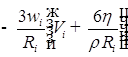0;

;

;

;

;

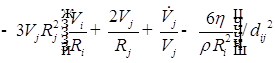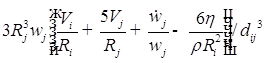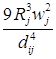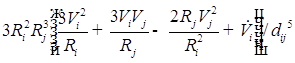Для второго уравнения:

;

=;

;

;

;

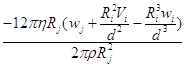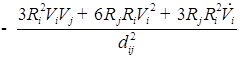
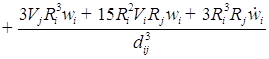
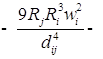
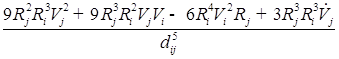
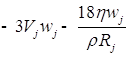
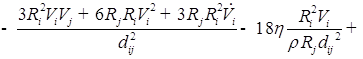
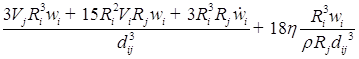
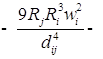
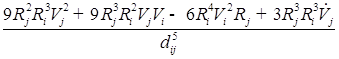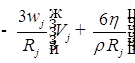0;

;

;

;

;

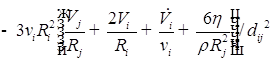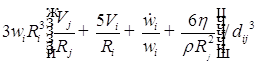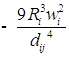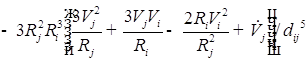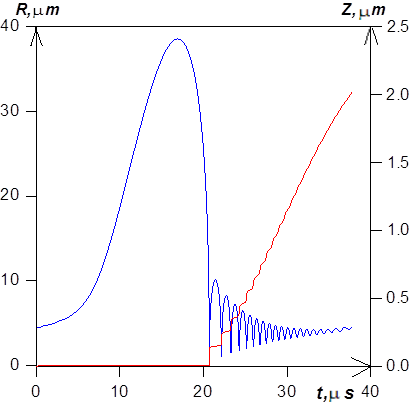
Рис.1. Изменение радиуса пузырька и положения его центра во времени.