Теория статистики

Содержание

 

1. Анализ рядов распределения

2. Анализ рядов динамики

3. Индексы

4. Выборочное наблюдение

Список литературы

1. Анализ рядов распределения

По данным ряда распределения своего вариант (табл. I) выполнить следующие расчеты. 1.1. Построить ряд распределения. Изобразить ряд графически в виде гистограммы (полигона) и кумуляты распределения. Сделать вывод о характере распределения. 1.2. Рассчитать моду, медиану, первый и третий квартиль. 1.3. Рассчитать средний уровень признака в совокупности; сравнить значение моды, медианы, средней и сделать вывод об асимметрии распределения. 1.4. Рассчитать показатели вариации: размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, коэффициент вариации. 1.5. Указать другие методы расчета среднего уровня и дисперсии. 1.6. Показать методику расчет дисперсии альтернативного признака. 1.7. Назвать виды дисперсии в совокупности, разбитой на группы, сформулировать правило их сложения и методику расчета показателя тесноты связи между изучаемыми признаками.

Решение

1.1. Построим ряд распределения.

 

Таблица А Распределение покупателей по стоимости покупок канцелярских товаров

Группы по стоимости покупок	Частота
18 – 24	18
24 – 28	27
28 – 32	35
32 – 36	41
36 – 40	30
40 – 44	21
44 и выше	15
Итого (объем ряда)	159

Гистограмма (полигон)

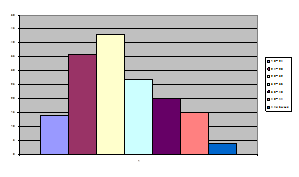
Кумулята распределения.

По виду графиков делаем вывод о нормальном распределении признака.

1.2. Рассчитаем моду, медиану, первый и третий квартиль.

Модальным является интервал (28, 32), содержащий наибольшее число покупателей. Модальный размер стоимости покупок:

Медиана определяется по формуле:

.

Медианным интервалом является интервал [28 - 32], содержащий -го покупателя. Медианный размер стоимости покупок:

=30,774.

Первый квартиль определяется по формуле:

Он задается интервалом [24 - 28], содержащим -го покупателя.

Третий квартиль определяется по формуле

Он задается интервалом [32 - 36], содержащим 3*-го покупателя.

1.3. Переходим от интервального ряда к моментному, приняв за стоимость покупок середину соответствующего интервала.

№ интервала	Середина Интервала ()	Число Покупателей ()
1	21	14	294
2	26	36	936
3	30	43	1290
4	34	27	918
5	38	20	760
6	42	15	630
7	46	4	184
Всего		159	5012

Находим средний уровень признака в совокупности по формуле средней арифметической взвешенной:

.

Получаем: 5012/159=31,522.

Так как мода и медиана меньше среднего уровня признака, то коэффициент асимметрии положителен.

1.4. Для расчетов показателей вариации составляем вспомогательную таблицу.

№ интервала	Середина интервала ()	Число покупателей ()
1	21	14	10,522	147,308	110,713	1549,978
2	26	36	5,522	198,792	30,493	1097,734
3	30	43	1,522	65,447	2,317	99,610
4	34	27	2,478	66,906	6,140	165,791
5	38	20	6,478	129,560	41,964	839,286
6	42	15	10,478	157,170	109,788	1646,823
7	46	4	14,478	57,912	209,612	838,448
Всего		159		823,094		6237,673

Размах вариации:

= 46 – 21=25.

Среднее линейное отклонение:

= 823,094/ 159 = 5,177,

Дисперсия:

 = 6237,673/ 159 = 39,231,

Среднее квадратическое отклонение

 = 6,263,

Коэффициент вариации

= 6,263*100/ 31,522 = 19,87%.

1.5. Методы расчета среднего уровня:

средний уровень ряда по формуле средней простой

,

по формуле средней хронологической

для моментных рядов; по формуле средней гармонической взвешенной

.

Дисперсию можно вычислить по формуле:

.

1.6. Рассчитать дисперсию альтернативного признака можно следующим образом: вычислить значения  и  Тогда .

1.7. В совокупности, разбитой на группы можно вычислить:

межгрупповую дисперсия по формуле:

среднюю из групповых дисперсий по формуле:

Правило сложения дисперсий

.

2. Анализ рядов динамики

2.1. Построить ряд динамики. Изобразить ряд в виде линейного графика. Сделать вывод о наличии тенденции изменения уровня и ее характере (увеличение уровня, снижение уровня, переломы тенденции, периоды одинакового типа тенденции).

2.2. Рассчитать среднюю хронологическую (ряд динамики интервальный). При разном направлении изменения уровней выделить однородные по тенденции периоды и рассчитать частные хронологические средние.

2.3. Рассчитать систему производных показателей ряда динамики (абсолютные приросты, темпы роста и прироста, абсолютные значения одного процента прироста).

2.4. Показать взаимосвязь цепных и базисных темпов роста и прироста.

2.5. Рассчитать средний абсолютный прирост. При разном направлении изменения уровней выделить однородные по тенденции периоды и рассчитать частные абсолютные приросты.

2.6. Рассчитать средний темп роста (три методики расчета). При разном направлении изменения уровней выделить однородные по тенденции периоды и рассчитать частные средние темпы роста.

2.7. Проанализировать тенденцию изменения уровня, самостоятельно избрав метод (скользящий средний уровень, аналитическое выравнивание по соответствующей модели). Выровненные значения показать на графике.

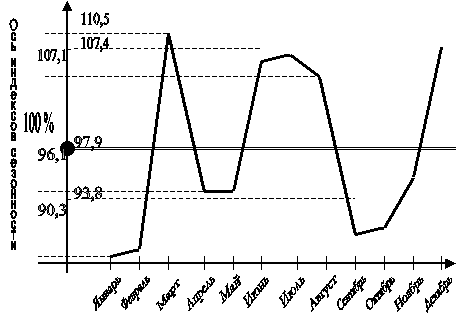
2.8. Проанализировать сезонные колебания объема выпуска продукции за три года. Рассчитать индексы сезонности. На графике изобразить сезонную волну.

Решение

2.1. Построим ряд динамики:

Годы	Выпуск продукции, тыс.усл.ед.
1	1476
2	1529
3	1607
4	1598
5	1673
6	1702
7	1680
8	1658
9	1612
10	1639

Изобразим ряд в виде линейного графика.

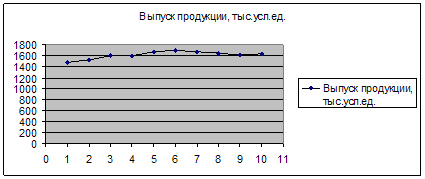
По графику делаем следующие выводы: Первые 6 лет наблюдалось небольшое увеличение выпуска, затем – снижение и в последний год - рост уровня выпуска.

2.2. Так как ряд динамики интервальный среднюю хронологическую вычисляем по формуле:

 = 16174/10= 1617,4.

Среднее первых 4 лет: (1476+1529+1607+1598)/4= 1552,5

Среднее последних 4 лет: (1680+1658+1612+1639)/4=1647,25

2.3. Рассчитаем систему производных показателей ряда динамики (абсолютные приросты, темпы роста и прироста, абсолютные значения одного процента прироста) по формулам:

Абсолютные приросты:

цепные: у_ц = у_i - y_i-1 базисные: у_б = у_i - y₀

 

Темпы роста:

цепные: Т_рц= (у_i / y_i-1 ) базисные: Т_рб= (у_i / y₀ )

 

Темпы прироста:

цепные: Т_пр = Dу_ц / у_i-1 , базисные: Т_пр = Dу_б / y₀

Абсолютное значение 1% прироста А_i= y_i-1 / 100

Составляем расчетную таблицу:

Годы	Выпуск продукции, тыс.усл.ед.	Абсолютные приросты		Темпы роста		Темпы прироста		Абсолют. значение 1%прироста ед. прод.
		Цеп.	Баз.	Цеп.	Баз.	Цеп.	Баз.
1	1476
2	1529	53	53	1,036	1,036	0,036	0,036	14,76
3	1607	78	131	1,051	1,089	0,051	0,089	15,29
4	1598	-9	122	0,994	1,083	-0,006	0,083	16,07
5	1673	75	197	1,047	1,133	0,047	0,133	15,98
6	1702	29	226	1,017	1,153	0,017	0,153	16,73
7	1680	-22	204	0,987	1,138	-0,013	0,138	17,02
8	1658	-22	182	0,987	1,123	-0,013	0,123	16,8
9	1612	-46	136	0,972	1,092	-0,028	0,092	16,58
10	1639	27	163	1,017	1,110	0,017	0,110	16,12
сумма	16174	163

2.4. Взаимосвязь цепных и базисных темпов роста и прироста:

2.5. Средний абсолютный прирост

исходя из цепных абсолютных приростов:

=163/9= 18,111

исходя из базисного абсолютного прироста:

=18,111.

Средний абсолютный прирост первых 6 лет: 226/5= 45,2

Средний абсолютный прирост последних 5 лет: (163-226)/4= -15,75

2.6. Средний темп роста:

(101,2%).

Средний темп прироста:

.

Средний темп роста первых 6 лет: .

Средний темп роста последних 5 лет: