Навигация
Министерство образования Республики Беларусь
Учреждение образования
«Гомельский государственный университет
им. Ф. Скорины»
Математический факультет
Кафедра МПУ
Распределение памяти
Курсовая работа
Исполнитель:
Студентка группы М-41 ____________ Кондратенко А.Ю.
Научный руководитель:
Канд. физ-мат. наук, доцент ____________ Гундарева Т.Е.
Гомель 2007
Содержание
Введение
1 Задача1.Алгоритм Дойча-Шорра-Уэйта
2 Задача 2. Пометка занятых ячеек памяти
3 Задача 3
3.1 Простое и неэффективное решение проблемы
3.2 Стратегия перераспределения памяти
3.3О структуре памяти
4 Метод близнецов
4.1 Главная идея
4.2 Шаг 5: Блок данных объёмом 4: 1, 1, 2, 3, 1, 4, 3, 5, 13, 21, 34, 55
Заключение
Литература
Введение
Подавляющее большинство программистов - это прикладные программисты, то есть люди полагающие, что исполнение написанной программы компьютером - это проблема компьютера. Встретив команду типа a:integer; компьютер должен её обработать, но в чём заключается эта обработка большинство из нас не слишком интересуется. Ещё меньше нас интересует и процесс выполнения таких команд как a:integer и new(a). Однако интуитивно мы все понимаем, (даже если не знаем точно), что за этими командами скрываются достаточно сложные процессы распределения и перераспределения оперативной памяти.
Особенно сложны проблемы управления для так называемой динамической памяти. Действительно, статические переменные (то есть те, которые описываются после ключевого слова var) создаются один раз, в момент запуска программы на выполнение и уничтожаются один раз, в момент окончания работы программы. Это означает, что проблемы перераспределения памяти просто не существует, всё определяется в начале и уже никогда не изменяется.
Однако статическая память это не вся память. Ещё существуют динамические переменные, которые можно, как создавать, так и уничтожить в процессе работы программы.
Итак, какие проблемы возникают при работе с динамическими переменными, как их решать и зачем их решать? Чтобы это понять, сделаем несколько важных замечаний:
Во-первых, в начале работы программы, доступная область памяти представляет собой сплошной пустой массив ячеек памяти.
Во-вторых, в момент создания динамической переменной, необходимая для неё память ищется в общей куче (это программисткий термин. Его английский вариант heap), при этом программа просматривает всю свободную память до тех пор, пока не обнаружит первый достаточно большой кусок свободной памяти.
В третьих, В момент уничтожения динамической переменной, используемые под неё ячейки просто возвращаются в общую кучу и при этом никакого перераспределения памяти не происходит.
Из этих трёх замечаний следует, что в процессе работы программы, если динамические переменные многократно создаются и уничтожаются, то куча динамической памяти будет представлять собой беспорядочное нагромождение свободных и занятых ячеек и может даже случится так, что при наличии большого объёма свободной памяти, разместить данное большого объёма не получится. Поясним это картинкой:
| ||||||
| ||||||
В имеющейся памяти, мы видим 5 свободных ячеек, однако нигде нет две свободных ячеек подряд, а стало быть нашу переменную, требующую две ячейки разместить некуда.
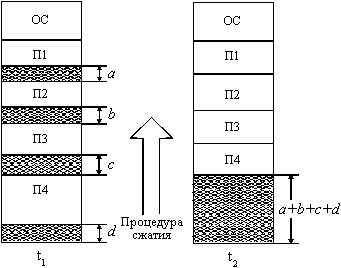
Если проблема понятна, то наверное понятно и то, как в принципе с ней нужно бороться. Нужно все свободные ячейки объединить в один массив свободной памяти. Если это сделать, то в нашем примере память будет выглядеть так:
![]()
Идея на первый взгляд очень проста, но при её реализации встречается ряд проблем, борьба с которыми может оказаться не вполне тривиальной.
Проблема 1.
С каждой занятой группой ячеек памяти связана специальная переменная именуемая указателем. Указатель содержит адрес этой группы, и если мы группу ячеек на которую указывает указатель переместим, то она для данного указателя окажется недоступной.
Проблема 2.
Различные группы ячеек, содержащие данные могут быть взаимосвязанными. Естественно, что при перераспределении памяти взаимосвязи между данными должны быть сохранены. Кстати из возможности существования связных списков данных следует ещё одна интересная проблема. Представьте себе простой связный список состоящий из двух связанных динамических переменных:
![]()
Группа ячеек памяти А непосредственно связана с указателем, то есть её местоположение известно конкретной переменной, чего нельзя сказать о группе В и группе С. И чтобы их обнаружить необходимо пройти по всей цепочке связного списка. А ведь связный список может быть произвольно сложный. Например, такой:
| |||||||
Попытка поиска занятых ячеек памяти в таком связном списке обязательно приведёт к зацикливанию (В, С, Е) если не позаботится специальным образом о обработке таких ситуаций.
Таким образом, мы видим, что необходимость перераспределения памяти действительно есть. Это, во-первых. Примеры, приведённые выше, показывают, что методы такого перераспределения не совсем уж тривиальны, а может быть и достаточно сложны. Это, во-вторых. Вот этими методами мы далее и займёмся.
1 Задача 1. Алгоритм Дойча-Шорра-Уэйта
Дан массив блоков памяти. Для каждого блока существует метка, отмечающая, свободен блок от данных или занят. Кроме того, некоторые из блоков имеют ссылки на другие блоки, то есть массив блоков занятых данными представляет собой один или несколько связных списков (графов) произвольной структуры. Необходимо собрать все блоки свободные от данных.
В чём будет заключаться решение:
Итак, мы имеем большой массив памяти в котором есть как пустые блоки, так и свободные. Нам нужно либо составить список свободных блоков, либо список занятых. Это вообщем-то идентичные задачи. Список результат может представлять собой несколько указателей содержащих адреса начала связного списка состоящего из свободных или наоборот занятых ячеек. Хотя, нам сейчас не столь важно, что будет представлять собой данный список, важно разобраться с тем, как его составить.
Общая идея
Пусть занятая память представляет собой некоторое количество связных списков, естественно исполнитель (как бы конкретно он ни работал) должен проходить все связные списки и для каждого делать следующее (пусть мы составляем список занятой памяти):
1. Перейти в очередной узел списка.
2. Записать информацию о узле в список занятой памяти.
3. Пока список узлов связанных с данным не исчерпан выполнять п.1
Совершенно, очевидно, что данный алгоритм (а точнее схема алгоритма ) имеет рекурсивный характер. Это означает, что для каждого узла списка будет создаваться собственная копия процедуры обработки узла (занесение информации в список-результат и переход на последующие узлы). И тут возникает серьёзная
Проблема
Паскаль, при каждом рекурсивном вызове процедуры или функции создаёт активационную запись, в которой сохраняет информацию о состоянии данных полученных в результате работы данной копии процедуры/функции. То есть, сколько будет вызовов (а их будет столько сколько узлов имеет список), столько будет активационных записей создано Паскаль-программой.
Все активационные записи хранятся в специальной структуре памяти - стеке, размер которого ограничен, по крайней мере, общим объемом оперативной памяти. А это означает, что при очень большой длине обрабатываемого связного списка (и кстати не обязательно разветвляющего, а может быть и линейного ) программе для запоминания промежуточных данных может понадобится больше памяти, чем её затрачено на анализируемые данные. А это означает потерю всякого смысла в обработке.
Хорошая идея
Хорошая идея напрашивается сама собой, нужно обойтись без рекурсии. Ниже мы рассмотрим две различные задачи. Первая задача будет о том как бороться со связным списком у котором из каждого узла может быть не более двух ответвлений. Вторым методом мы попробуем справится с более общей задачей, то есть таким связным списком в котором из каждого узла выходит много указателей.
Примечание: Этот материал представляет собой конспект главы из книги "Структуры данных и алгоритмы" авторов: Альфред В. Ахо; Джон Э. Хопкрофт; Джеффри Д. Ульман
Я только позволил себе в некоторых местах вставить дополнительные пояснения, так как посчитал их изложение слишком сложным. Надеюсь, мои пояснения не сделали изложение ещё менее понятным.
Мои предварительные пояснения:
Основным объектом обрабатываемым алгоритмом является структура состоящая из двух ячеек (left, right) указывающих на последующие ячейки, ячеек данных и ячейки содержащей пометку занята ячейка или свободна. То есть мы имеем дело с двоичным деревом. Может показаться, что это всего лишь частный случай. Однако это не так, если вспомнить, что любую древовидную структуру можно преобразовать в двоичное дерево. Ниже приведён пример двух эквивалентных структур данных. Эквивалентных в том смысле, что они содержат одинаковое количество содержательных данных и имеют одинаковое количество связей.
Общая идея алгоритма такова: необходимо запоминать путь, по которому идёт алгоритм, чтобы иметь возможность вернуться к ячейке источнику. Для этого можно использовать имеющиеся указатели left, right а именно тот из них который уже использован для продвижения вперёд. Но так как в разных узлах может быть разная ситуация с этими указателями, то необходимо запоминать какой из них используется в конкретной ячейке для запоминания пути обратно. В алгоритме для этого предназначено специальное поле back.
Таким образом, вместо стека активационных записей можно использовать поля указателей ячейки, анализируемой в настоящий момент, можно использовать поля указателей вдоль этого пути, которые и будут формировать путь. Таким образом, каждая ячейка, за исключением последней, содержит или в поле left, или в поле right указатель на её предшественника - ячейку расположенную ближе к ячейке source. Мы опишем алгоритм, использующий ещё одно битовое поле, которое называется back. Поле это имеет перечислимый тип (L, R) и говорит о том, какое из полей, left или right, указывает на предшественника.
Эта процедура, исполняющая нерекурсивный поиск в глубину использует указатель current для указания на текущую ячейку, а указатель previous - для указания на предшественника текущей ячейки. Переменная source указывает на ячейку source1, которая содержит только указатель в своем правом поле. До выполнения маркировки в ячейке source1 значение поля back устанавливаем равным R, а её правое поле указывает на самого себя. На ячейку на которую обычно указывает source1 теперь указывает ячейка current, а на source1 указывает previous. Операция маркировки прекращается в том случае, когда current=previous, это может произойти лишь при условии, если обе ячейки current и previous указывают на source1 то есть уже просмотрена вся структура.
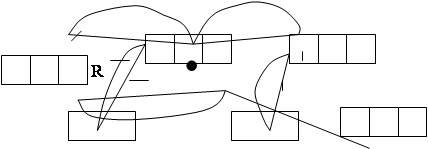
1. Движение вглубь. Если текущая ячейка имеет один или несколько не пустых указателей, то нужно перейти на первый из них, то есть следовать указателю в поле left или, если его нет, то указателю в поле right. Теперь надо преобразовать ячейку на которую указывает текущая ячейка, в новую текущую ячейку, а старую текущую в предыдущую. Чтобы облегчить поиск пути обратно, нужно сделать так, чтобы указатель, которому мы только что следовали, теперь указывал на прежнюю предыдущую ячейку. Эти изменения показаны на рисунке А.
2. Переключение. Если мы определили, что ячейки, исходящие из текущей ячейки, уже все просмотрены, то обращаемся к полю back предыдущей ячейки. Если его значение равно L, а поле right этой ячейки содержит ненулевой указатель на какую-то ячейку C, то делаем С текущей ячейкой, в то время как статус предыдущей ячейки остаётся неизменным. Но значение поля back предыдущей устанавливаем равным R, а левый указатель в этой ячейке устанавливаем так, чтобы он указывал на прежнюю текущую ячейку. Чтобы отследить и сохранить путь от предыдущей ячейке, обратно к ячейке source, надо сделать так, чтобы указатель на ячейку С в поле right в предыдущей ячейке теперь указывал туда, куда указывал ранее её левый указатель. Эти изменения показаны на рис Б.
3. Отход. Если мы определили, что ячейки, исходящие из текущей ячейки, уже просмотрены, но значение поля back предыдущей ячейки равно R или L, а поле right содержит атом (Атомом авторы называют содержательное данное) или нуль указатель, значит мы уже просмотрели все ячейки, исходящие из предыдущей ячейки. Тогда осуществляется отход, при котором предыдущая ячейка становится текущей, а следующая ячейка вдоль пути от предыдущей к ячейке source - новой предыдущей ячейкой. Эти изменения показаны на рисунке В
Нетрудно заметить, что каждый шаг, показанный на рисунке, можно рассматривать как одновременную циклическую перестановку трёх указателей. Чтобы выполнить эти модификации указателей, используется процедура rotate
Procedure rotate(var p1, p2, p3: ^celltype);
Var
Temp: celltype;
Begin
Temp:=p1;
P1:=p2;
P2:=p3;
P3:=temp;
End;
Теперь вернёмся к описанию нерекурсивной процедуры маркировки. Для неё возможны два состояния: продвижение вперёд, представленное меткой state1 и отход представленный меткой state2 и отход представленный меткой state2. Поначалу, а также в тех случаях, когда мы перешли на новую ячейку (либо в результате шага продвижения вперёд, либо в результате шага переключения), мы переходим в первое состояние. В этом состоянии мы пытаемся выполнить ещё один шаг продвижения вперёд и "отходим" или "переключаемся" лишь в том случае, если оказываемся заблокированными. Можно оказаться заблокированными по двум причинам: (1) ячейка к которой только, что обратились , уже помечена; (2)в данной ячейке отсутствуют ненулевые указатели. Оказавшись заблокированными, переходим во второе состояние - состояние отхода. Переход во второе состояние возможен в тех случаях, когда мы отходим или когда не можем оставаться продвижения вперёд, так как оказались заблокированными. В состоянии отхода проверяем, отошли ли обратно на ячейку source1. Как уже было сказано выше, мы распознаём эту ситуацию по выполнению условия previous=current; в этом случае переходим в состояние 3 (метка state3), то есть практически закончили маркировку ячеек. В противном случае принимается решение либо отступить и остаться в состоянии отхода, либо переключится и перейти в состояние продвижения вперёд.
![]()
![]()
![]()



![]()
![]()
![]()
![]()
![]()
![]()
![]() А) движение вперёд
А) движение вперёд
|
| ||||||||||||||||||
На рисунках старые указатели показаны сплошными линиями, а новые пунктирными.
Б) Переключение
 | |||||||||||
| |||||||||||
| |||||||||||
В) Отход
 | |||||
| |||||
| |||||
Авторы используют следующие обозначения: PP - указатель/указатель; PA - указатель/атом и т.д. Кроме того можно заметить, что текст записанный ниже, это не вполне Паскаль-программа. Там не всё в порядке с оператором возврата из процедуры. Например return(false); это авторы делают для упрощения записи. Понимать этот оператор надо так:
Имя функции:=false;
Goto метка конца тела функции.
function blockleft (cell:celltype):boolean;
{Проверяет, является ли левое поле атомом или нуль указателем}
begin
with cell do
if (pattern=pp) or (pattern=pa) then
if left<>nil then return(false);
return true;
end; {blockleft}
function blockright (cell:celltype): boolean;
{ Проверяет, является ли левое поле атомом или нуль указателем }
begin
with cell do
if (pattern=pp) or (pattern=ap) then
if right<>nil then return(false);
end;{blockright}
function block (cell:celltype):boolean;
{проверяет, помечена ли ячейка и не содержит ли ненулевые указатели}
begin
if (cell.mark=true) or blockleft(cell) and blockright(cell) then
return true
else return false
end; {block}
procedure nrdfs; {помечает ячейки, доступные из ячейки source}
var
current, previous:^celltype;
begin {инициализация}
current:=source1^.right; {ячейка на которую указывает source1}
previous:=source1;
source1^.back:=r;
source1^.right:=source1;
source1^.mark:=true;
state1: {Движение вперёд}
if block (current^) then
begin {Подготовка к отходу}
current^.mark:=true;
goto state2;
end;
else
begin
{пометить и продвинуться вперёд}
current^.mark:=true;
if blockleft (current^) then
begin
{следование правому указателю}
current^.back:=r;
rotate (previous, current, current^.right);
{реализация изменения согласно схеме а}
goto state1
end
else
begin
{следование левому указателю}
current^.back:=L;
rotate(previous, current, current^.left);
{реализация изменения согласно схеме а}
goto state1;
end;
end;
state2: {Завершение отход или переключение}
if previous = current then goto state3 {завершение}
else if (previouse^.back=L) and (not blockright(previous^)) then
begin {переключение}
previous^.back:=R;
rotate(previouse^.left,current, previouse^.right);
{реализация изменений как на схеме б}
goto state1;
end
else if previous^.back=R then {Отход}
rotate(previous, previous^.right,current)
{реализация изменений как на схеме в}
else rotate(previous, previous^.left,current);
{реализация изменений вариант в, но поле left предыдущей ячейки включено в путь}
goto state2
end;
state 3: {Здесь необходимо вставить код для связывания непомеченных ячеек в список свободной памяти}
end; {nrdfs}
Похожие работы
... 12 Библиографический список................................................................. 15 Введение Целью работы является демонстрация работы с динамической памятью на примере программ разработанных к заданиям 2, 6, 8, 10, 12, 14, 16 из методического указания [1]. Динамическое распределение памяти предоставляет программисту большие возможности при обращении к ресурсам памяти в ...
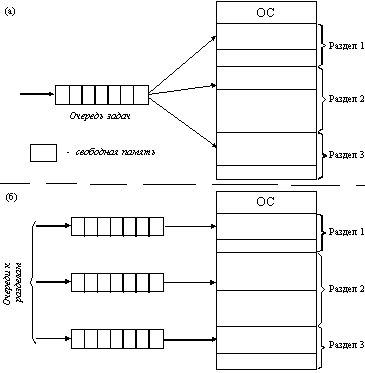
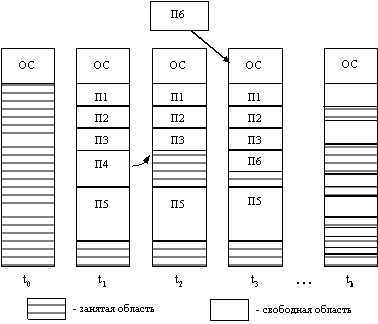
... задачи П4 место загружается задача П6, поступившая в момент t3. Рис. 2.10. Распределение памяти динамическими разделами Задачами операционной системы при реализации данного метода управления памятью является: ведение таблиц свободных и занятых областей, в которых указываются начальные адреса и размеры участков памяти, при поступлении новой задачи - анализ запроса, просмотр ...
... .) В системах, в которых страницы инструкций (в противоположность страницам данных) являются реентерабельными, бит изменения никогда не устанавливается. 2. Разработка алгоритма управления оперативной памятью Ниже приведён алгоритм управления оперативной памятью в системе Linux. В основе всего лежат страницы памяти. В ядре они описываются структурой mem_map_t. typedef struct page { /* ...
... новые следы памяти могут поступать в активном или неактивном состоянии. Именно это свойство лежит в основе исключительно важного феномена — так называемого латентного обучения. Концепция состояний памяти свободна от условного деления на кратковременную и долговременную и потому может объяснять феномены, которые остаются непонятными с точки зрения временного подхода к организации памяти. То, что ...
0 комментариев