Навигация
Решение задачи с помощью математической модели и средств MS Excel
Содержание
Введение
Условие задачи
Математическая модель задачи
Аналитическое исследование функции. Нахождение критических точек
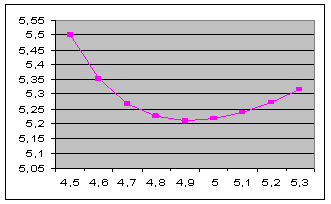
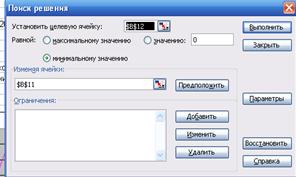
Построение графика искомой функции средствами MS Excel
Вывод
Используемая литература
Введение
В данной работе требуется решить математическую задачу двумя способами, один - это привычный для нас вариант, с помощью математических исследований, а второй - с помощью специального офисного приложения MS Excel. Для этого нам необходимо:
составить математическую модель задачи,
определить исследуемую функцию, зависящую от одной переменной,
построить график заданной функции с помощью графического редактора MS Excel,
исследовать функцию по общей схеме, найти критические точки,
найти решение задачи,
сделать вывод, сравнить полученные результаты.
Условие задачи
Кривая полных издержек имеет вид ![]() (где х - объем производства). Рассчитать, при каком объеме производства средние издержки минимальны.
(где х - объем производства). Рассчитать, при каком объеме производства средние издержки минимальны.
Математическая модель задачи
Целью любого производителя является максимизация прибыли. Главным препятствием к достижению этого является спрос на готовую продукцию и издержки производства.
Средние издержки - это издержки на единицу продукций.
Средние постоянные издержки (AFC) определяются путем деления суммарных постоянных издержек (TFC) на соответствующее количество произведенной продукций (Q).
AFC = TFC / Q
Так как постоянные издержки по определению не зависят от объема выпускаемой продукций, то и средние постоянные издержки будут уменьшаться с увеличением объема производства
Средние переменные издержки (AVC) определяются путем деления суммарных переменных издержек (TVC) на соответствующее количество произведенной продукций Q.
AVC = TVC / Q
AVC сначала падают, достигают своего минимума, а затем начинают расти. Такой наклон кривой объясняется законом убывающей доходности т.е. до четвертой единицы предельные издержки падают, следовательно и AVC так же будут падать, а начиная с пятой единицы как TVC так и AVC начинают возрастать.
Средние общие издержки (ATC) рассчитываются при помощи деления общих издержек TC на объем произведенной продукций Q или же соотношением AFC и AVVC для каждого из возможных способов производства.
ATC = TC / Q = AFC + AVC
Введем необходимые обозначения и составим исходную функцию от одной переменной.
Получим, что средние издержки будут вычисляться по формуле:

Т. е. исследуем функцию вида:
![]()
Воспользуемся общей схемой исследования функции.
![]()
1. Найти область определения
Областью определения будут числа больше 0, т.к объем производства должен быть положительным, т.е. ![]() . Получим, что
. Получим, что
![]()
2. Найти (если это можно) точки пересечения графика с осями координат.
В нашем случае это невозможно, т.к ![]() , а решая квадратное уравнение вида
, а решая квадратное уравнение вида ![]() получаем мнимые корни (т.е. дискриминант меньше 0), следовательно, точек пересечения с осями координат нет.
получаем мнимые корни (т.е. дискриминант меньше 0), следовательно, точек пересечения с осями координат нет.
3. Найти интервалы знакопостоянства функции (промежутки, на которых ![]() или
или ![]() ). Координаты вершины параболы (3;
). Координаты вершины параболы (3;
6), значит, ![]() при
при ![]() , и
, и ![]() при
при ![]() .
.
4. Выяснить является ли функция четной, нечетной или общего вида.
Функция ![]() является функцией общего вида, т.к
является функцией общего вида, т.к
![]()
5. Найдите асимптоты графика функции.
Функция ![]() не имеет вертикальной, горизонтальной и наклонной асимптот.
не имеет вертикальной, горизонтальной и наклонной асимптот.
6. Найдите интервалы монотонности функции.
Для этого найдем первую производную от заданной функции:
![]()
![]()
Решим уравнение вида:

![]()
Получим, что в точке ![]() функция меняется, т.е. на промежутке
функция меняется, т.е. на промежутке ![]() функция монотонно убывает, а на
функция монотонно убывает, а на ![]() возрастает.
возрастает.
Похожие работы
... все поставленные цели и задачи. В ходе выполнения были сделаны следующие выводы. Решив данную задачу, двумя способами, мы получили равные результаты. В первом случае, в процессе решения задачи самостоятельно, мы потеряли достаточное количество времени, сохраняя большой риск ошибки в вычислениях. Во втором же, решение задачи с помощью MS Excel, мы достигли того же результата минимизируя
... 0 505/103 0 792/103 669/103 500/103 Анализ Таблицы 6 позволяет сделать вывод о допустимости и оптимальности базиса XБ4=(x5, x7, x1, x2, x4)T. 3.4 Результат решения задачи планирования производства В результате решения поставленной задачи симплекс-методом получили набор производимой продукции x=(x1, x2, x3, x4, x5)=( 15145/103, 8910/103, 0, 1250/103, 3255/103), который удовлетворяет всем ...
... в больших объемах потребляет разнообразные запасные части для поддержания активной части своих производственных фондов в работоспособном состоянии. Запасные части для предприятий железнодорожного транспорта изготавливаются на заводах по ремонту подвижного состава и производству запасных частей и других специализированных предприятиях. Снижение издержек, связанных с обеспечением предприятий ...
... с помощью программы оптимизатора в Excel и в системе Mathcad. Анализ оптимального плана и решение менеджера. Оптимальными планами являются решения, полученные с помощью программ Excel и Mathcad, которые получили одинаковый результат: Судна первого типа – 4 штуки, судов второго типа – 2 штуки. Прибыль будет составлять 140000000 руб. При нахождении оптимального плана пассажировместимость ...
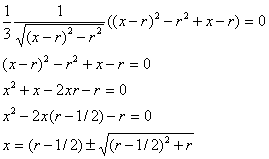
0 комментариев