Навигация
Розробка математичної програми в середовищі С++
Вступ
Математичне моделювання займає вагоме місце серед інших програм які створюються програмістами. Під таким моделюванням розуміють сукупність математичних співвідношень таких як формули, рівняння, логічні вирази, які визначають характеристики і властивості системи, об’єкта, процесу або ж їх витікаючих, також функціонування залежно від параметрів компонентів, початкових умов, вхідних змін і часу. Загалом математична модель описує функціональну залежність між вихідними залежними змінними, через які відображається функціонування системи, незалежними і змінюваними змінними а також вхідними змінами, які мали вплив на систему.
Для окремого завдання формулюється окрема незалежна математична задача. В загальних випадках, коли функціональна залежність для множини вхідних даних що виступають як множина аргументів, задана неявно, за допомогою математичної моделі необхідно визначити множину вихідних залежних змінних, що виступають як множини значень функцій. При цьому відповідно до виду математичної моделі розрізняють такі базові типи математичних задач: розв’язання системи лінійних рівнянь, алгебраїчних рівнянь, апроксимація, інтегрування, диференціювання, системи диференційних рівнянь і ін. На сьогодні, більшість громіздких і трудоємких робіт по обчисленню різноманітних функцій і виразів, покладається на комп’ютер, але для простішого його використання потрібна програма, тобто зв’язний алгоритм дій, який має створити програміст.
Фізика, хімія, біологія, астрономія, геометрія та багато інших наук використовують спеціальні програми призначені для підрахунку величин в залежності від різних вхідних даних, на основі математичних задач.
Дана курсова робота описує один з типів такого моделювання, а саме розв’язанню нелінійних алгебраїчних рівнянь. Для розв’язання даного рівняння було обрано метод хорд.
1. Аналіз завдання та розробка методу вирішення задачі
Нехай дано рівняння ![]() і нехай
і нехай ![]()
![]() - його дійсний корінь, тобто
- його дійсний корінь, тобто ![]() Геометрично рівність
Геометрично рівність ![]() означає, що графік функції
означає, що графік функції ![]() проходить через точку
проходить через точку ![]() осі
осі![]() . Далі ми будемо розв’язувати задачу про знаходження
. Далі ми будемо розв’язувати задачу про знаходження ![]() з наперед заданою точністю наближеного значення кореня рівняння
з наперед заданою точністю наближеного значення кореня рівняння ![]() Спочатку розглянемо питання про відокремлення коренів рівняння.
Спочатку розглянемо питання про відокремлення коренів рівняння.
Корінь рівняння ![]() відокремлений, якщо знайдено відрізок (позначимо його
відокремлений, якщо знайдено відрізок (позначимо його ![]() ), в якому, крім
), в якому, крім ![]() , немає інших коренів цього рівняння.
, немає інших коренів цього рівняння.
Задача відокремлення коренів рівняння ![]() розв’язується просто, якщо побудова графіка функції
розв’язується просто, якщо побудова графіка функції ![]() не є важкою. Дійсно, маючи графік функції
не є важкою. Дійсно, маючи графік функції ![]() , легко виділити відрізки, в кожному із яких знаходиться лише один корінь розглядуваного рівняння, або, що те саме, виділити відрізки, на кожному із яких є лише одна точка перетину кривої
, легко виділити відрізки, в кожному із яких знаходиться лише один корінь розглядуваного рівняння, або, що те саме, виділити відрізки, на кожному із яких є лише одна точка перетину кривої ![]() з віссю
з віссю![]() .
.
Відділити корені рівняння ![]() при умові, що
при умові, що ![]() - диференційована функція, можна не лише графічно. Нехай на кінцях деякого відрізка
- диференційована функція, можна не лише графічно. Нехай на кінцях деякого відрізка![]() функція
функція ![]() має значення різних знаків. Тоді за властивістю неперервних функцій ця функція на інтервалі
має значення різних знаків. Тоді за властивістю неперервних функцій ця функція на інтервалі ![]() по меншій мірі один раз обертається в нуль, тобто рівняння
по меншій мірі один раз обертається в нуль, тобто рівняння ![]() має по меншій мірі один корінь.
має по меншій мірі один корінь.
Якщо похідна ![]() зберігає знак на відрізку
зберігає знак на відрізку ![]() , то внаслідок монотонності функції
, то внаслідок монотонності функції ![]() рівняння
рівняння ![]() на інтервалі
на інтервалі ![]() має єдиний корінь.
має єдиний корінь.
У цьому випадку числа ![]() та
та![]() є наближеними значеннями кореня
є наближеними значеннями кореня ![]() відповідно з нестачею і з надлишком. Ці інтервали можна звужувати, тоді границі їх будуть давати все точніші наближення для коренів рівняння.
відповідно з нестачею і з надлишком. Ці інтервали можна звужувати, тоді границі їх будуть давати все точніші наближення для коренів рівняння.
Нехай корінь ![]() рівняння
рівняння ![]() відокремлений, тобто є відрізок
відокремлений, тобто є відрізок ![]() , на якому, крім
, на якому, крім ![]() , немає інших коренів цього рівняння.
, немає інших коренів цього рівняння.
Відшукаємо значення ![]() з будь-якою точністю за таких допущень: функція
з будь-якою точністю за таких допущень: функція ![]() має на відрізку
має на відрізку ![]() неперервні похідні до другого порядку включно і, крім того, похідні
неперервні похідні до другого порядку включно і, крім того, похідні ![]() і
і ![]() зберігають знаки на цьому відрізку. Із цих умов випливає, що
зберігають знаки на цьому відрізку. Із цих умов випливає, що ![]() - монотонна функція на відрізку
- монотонна функція на відрізку ![]() , яка на кінцях має різні знаки, а також, що крива
, яка на кінцях має різні знаки, а також, що крива ![]() опукла або вгнута (рис. 1.1).
опукла або вгнута (рис. 1.1).
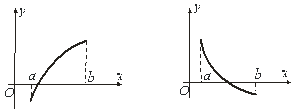
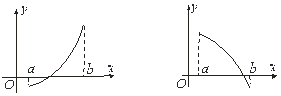
Рисунок 1.1 – Варіанти поведінки функції ![]()
Отже, розглянемо задачу знаходження коренів рівняння
![]() , (1)
, (1)
де ![]() - задана функція дійсного змінного.
- задана функція дійсного змінного.
Розв’язування даної задачі можна розкласти на декілька етапів:
а) дослідження розташування коренів (в загальному випадку на комплексній площині) та їх кратність;
б) відділення коренів, тобто виділення областей, що містять тільки один корінь;
в) обчислення кореня з заданою точністю за допомогою одного з ітераційних алгоритмів.
Далі розглядаються ітераційні процеси, що дають можливість побудувати числову послідовність xn, яка збігається до шуканого кореня ![]() рівняння (1).
рівняння (1).
Нехай ![]() і відомо, що рівняння (1) має єдиний корінь
і відомо, що рівняння (1) має єдиний корінь ![]() . Покладемо a0=a, b0=b, x0=(a0+b0)/2. Якщо
. Покладемо a0=a, b0=b, x0=(a0+b0)/2. Якщо ![]() , то
, то ![]() . Якщо
. Якщо ![]() , то покладемо
, то покладемо
 (2)
(2)
 (3)
(3)
![]() (4)
(4)
і обчислимо ![]() . Якщо
. Якщо ![]() , то ітераційний процес зупинимо і будемо вважати, що
, то ітераційний процес зупинимо і будемо вважати, що ![]() . Якщо
. Якщо ![]() , то повторюємо розрахунки за формулами (2) – (4).
, то повторюємо розрахунки за формулами (2) – (4).
З формул (2), (3) видно, що ![]() і
і ![]() . Тому
. Тому ![]() , а отже шуканий корінь
, а отже шуканий корінь ![]() знаходиться на проміжку
знаходиться на проміжку ![]() . При цьому має місце оцінка збіжності
. При цьому має місце оцінка збіжності
![]() . (5)
. (5)
Звідси випливає, що кількість ітерацій. які необхідно провести для знаходження наближеного кореня рівняння (1) з заданою точністю e задовольняє співвідношенню
 . (6)
. (6)
де [c] - ціла частина числа c.
Серед переваг даного методу слід відзначити простоту реалізації та надійність. Послідовність {xn} збігається до кореня ![]() для довільних неперервних функцій f(x). До недоліків можна віднести невисоку швидкість збіжності методу та неможливість безпосереднього узагальнення систем нелінійних рівнянь.
для довільних неперервних функцій f(x). До недоліків можна віднести невисоку швидкість збіжності методу та неможливість безпосереднього узагальнення систем нелінійних рівнянь.
Метод простої ітерації застосовується до розв’язування нелінійного рівняння виду
![]() . (7)
. (7)
Перейти від рівняння (1) до рівняння(7) можна багатьма способами, наприклад, вибравши
![]() , (8)
, (8)
де ![]() - довільна неперервна функція.
- довільна неперервна функція.
Вибравши нульове наближення x0, наступні наближення знаходяться за формулою
![]() . (9)
. (9)
Наведемо достатні умови збіжності методу простої ітерації.
Теорема 1. Нехай для вибраного початкового наближення x0 на проміжку
![]() (10)
(10)
функція j(x) задовольняє умові Лівшиця
![]() (11)
(11)
де 0<q<1, і виконується нерівність
![]() . (12)
. (12)
Тоді рівняння (7) має на проміжку S єдиний корінь ![]() , до якого збігається послідовність (9), причому швидкість збіжності визначається нерівністю
, до якого збігається послідовність (9), причому швидкість збіжності визначається нерівністю
 . (13)
. (13)
Зауваження: якщо функція j(x) має на проміжку S неперервну похідну ![]() , яка задовольняє умові
, яка задовольняє умові
![]() , (14)
, (14)
то функція j(x) буде задовольняти умові (11) теореми 1.
З (13) можна отримати оцінку кількості ітерацій. які потрібно провести для знаходження розв’язку задачі (7) з наперед заданою точністю e:
 . (15)
. (15)
Наведемо ще одну оцінку. що характеризує збіжність методу простої ітерації:
 . (16)
. (16)
Для збіжності ітераційного процесу (9) суттєве значення має вибір функції j(x). Зокрема, якщо в (8) вибрати ![]() , то отримаємо метод релаксації.
, то отримаємо метод релаксації.
![]() , (17)
, (17)
який збігається при
![]() . (18)
. (18)
Якщо в деякому околі кореня виконуються умови
![]() , (19)
, (19)
то метод релаксації збігаються при ![]() . Збіжність буде найкращою при
. Збіжність буде найкращою при
![]() . (20)
. (20)
При такому виборі t для похибки ![]() буде мати місце оцінка
буде мати місце оцінка
![]() , (21)
, (21)
де ![]() .
.
Кількість ітерацій, які потрібно провести для знаходження розв’язку з точністю e визначається нерівністю
 . (22)
. (22)
Зауваження: якщо виконується умова ![]() , то ітераційний метод (17) потрібно записати у вигляді
, то ітераційний метод (17) потрібно записати у вигляді ![]() .
.
Метод Ньютона застосовується до розв’язування задачі (1), де f(x) є неперервно-диференційованою функцією. На початку обчислень вибирається початкове наближення x0. Наступні наближення обчислюються за формулою
 . (23)
. (23)
З геометричної точки зору xn+1 є значенням абсциси точки перетину дотичної до кривої y=f(x) в точці (xn, f(xn)) з віссю абсцис. Тому метод Ньютона називають також методом дотичних.
Теорема 2. Якщо ![]() не змінює знака на [a, b], то виходячи з початкового наближення
не змінює знака на [a, b], то виходячи з початкового наближення ![]() , що задовольняє умові
, що задовольняє умові ![]() , можна обчислити методом Ньютона єдиний корінь
, можна обчислити методом Ньютона єдиний корінь ![]() рівняння (1) з будь-якою степінню точності.
рівняння (1) з будь-якою степінню точності.
Теорема 3. Нехай ![]() - простий дійсний корінь рівняння (1) і
- простий дійсний корінь рівняння (1) і ![]() , де
, де ![]() ,
,
![]() , (24)
, (24)
причому
 . (25)
. (25)
Тоді для ![]() метод Ньютона збігається, причому для похибки справедлива оцінка
метод Ньютона збігається, причому для похибки справедлива оцінка
![]() . (26)
. (26)
З оцінки (26) видно, що метод Ньютона має квадратичну збіжність, тобто похибка на (n+1) – й ітерації пропорційна квадрату похибки на n-й ітерації.
Модифікований метод Ньютона
![]() (27)
(27)
дозволяє не обчислювати похідну ![]() на кожній ітерації, а отже і позбутися можливого ділення на нуль. Однак цей алгоритм має тільки лінійну збіжність.
на кожній ітерації, а отже і позбутися можливого ділення на нуль. Однак цей алгоритм має тільки лінійну збіжність.
Кількість ітерацій, які потрібно провести для знаходження розв’язку задачі (1) з точністю e задовольняє нерівності
 . (28)
. (28)
Похожие работы
... Хлопчики 9 8 Дівчинки 4 5 Середній вік 1,8 1,7 Середній рівень (М ± m) активності основних психомоторних функцій 14 ± 2 14 ± 3 Для реабілітації дітей була розроблена програма, яка включає додатковий догляд за дитиною, масажні вправи, комплексні гімнастичні заходи, а також додаткові заняття на розвиток уваги та рухливості. Комплекс гімнастичних та масажних вправ наведено в додатку А. ...
... і над плановим. Відомо, що собівартість є одним з головних джерел резервів підвищення ефективності роботи підприємства. Звідси сформуємо мету і задачі даної роботи. Метою даної роботи є підвищення ефективності роботи підприємства ВАТ «Дніпрополімермаш» шляхом управління собівартістю продукції. Відповідно, для досягнення поставленої мети необхідно вирішити наступні задачі: 1. Проаналізувати ...
... випадків, аварій, а з цим і простоїв на підприємстві, укріпити та створити культуру трудової діяльності. Виконання та розробка дипломного проекту “ Розробка дослідження системи керування електроприводом змінного струму дизель-потягу з використанням нейронних мереж ” відбувається за допомогою комп'ютера, тому питання охорони праці розглядаються щодо забезпечення здорових і безпечних умов роботи ...
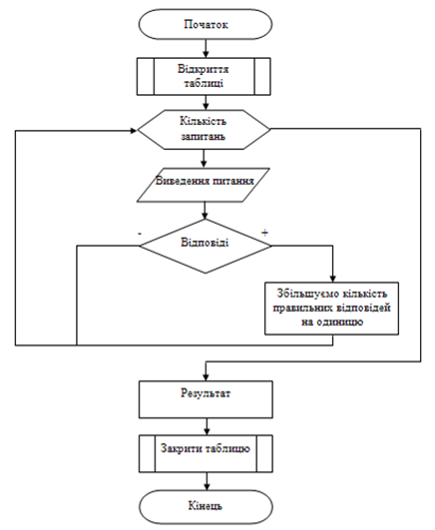
... його. Наприклад, вводимо назву виробу, норму витрат та кількість виробів – і перевіряємо обчислену потребу матеріалу. Програма цієї курсової роботи з дисципліни «Системне програмування та операційні системи» призначена для перевірки тестового контролю знань. Кожне запитання тесту може мати кілька варіантів відповідей: 1. Набір програмних модулів, які дозволяють керувати машиною? операційна ...










0 комментариев