Навигация
Вычислительная техника и программирование
КУРСОВАЯ РАБОТА
по теме: "Вычислительная техника и программирование"
Киев
Введение
Если задана функция y(x), то это означает, что любому допустимому значению х сопоставлено значение у. Но нередко оказывается, что нахождение этого значения очень трудоёмко. Например, у(х) может быть определено как решение сложной задачи, в которой х играет роль параметра или у(х) измеряется в дорогостоящем эксперименте. При этом можно вычислить небольшую таблицу значений функции, но прямое нахождение функции при большом числе значений аргумента будет практически невозможно. Функция у(х) может участвовать в каких-либо физико-технических или чисто математических расчётах, где её приходится многократно вычислять. В этом случае выгодно заменить функцию у(х) приближённой формулой, то есть подобрать некоторую функцию j(х), которая близка в некотором смысле к у(х) и просто вычисляется. Затем при всех значениях аргумента полагают у(х)"j(х).
Что касается критерия согласия, то классическим критерием согласия является "точное совпадение в узловых точках". Этот критерий имеет преимущество простоты теории и выполнения вычислений, но также неудобство из-за игнорирования шума (погрешности, возникающей при измерении или вычислении значений в узловых точках). Другой относительно хороший критерий — это "наименьшие квадраты". Он означает, что сумма квадратов отклонений в узловых точках должна быть наименьшей возможной или, другими словами, минимизирована. Этот критерий использует ошибочную информацию, чтобы получить некоторое сглаживание шума. Третий критерий связывается с именем Чебышева. Основная идея его состоит в том, чтобы уменьшить максимальное отклонение до минимума. Очевидно, возможны и другие критерии.
Цель задачи о приближении (интерполяции): данную функцию у(х) требуется приблизительно заменить некоторой функцией j(х), свойства которой нам известны так, чтобы отклонение в заданной области было наименьшим. интерполяционные формулы применяются, прежде всего, при замене графически заданной функции аналитической, а также для интерполяции в таблицах.
Один из подходов к задаче интерполяции — метод Лагранжа. Основная идея этого метода состоит в том, чтобы прежде всего найти многочлен, который принимает значение 1 в одной узловой точке и 0 во всех других. Легко видеть, что функция (1) является требуемым многочленом степени n; он равен 1, если X=Xj и 0, когда X=Xi, i¹j.
|
| (1) |
Многочлен Lj(x)×Yj принимает значения Yi в i-й узловой точке и равен 0 во всех других узлах. Из этого следует, что (2) есть многочлен степени n, проходящий через n+1 точку (Xi, Yi).
|
| (2) |
Другой подход — метод Ньютона (метод разделённых разностей). Этот метод позволяет получить аппроксимирующие значения функции без построения в явном виде аппроксимирующего полинома. В результате получаем формулу для полинома Pn, аппроксимирующую функцию f(x):
P(x)=P(x0)+(x-x0)P(x0,x1)+(x-x0)(x-x1)P(x0,x1,x2)+…+
(x-x0)(x-x1)…(x-xn)P(x0,x1,…,xn);
|
| разделённая разность 1-го порядка; |
|
| разделённая разность 2-го порядка и т.д. |
Значения Pn(x) в узлах совпадают со значениями f(x)
Фактически формулы Лагранжа и Ньютона порождают один и тот же полином, разница только в алгоритме его построения.
Постановка задачи:
1. Построить интерполяционный полином Ньютона по значениям функции в узлах: ![]() .
.
2. Математическая постановка задачи:
Формула выглядит так:
![]()
Разделённая разность:
 .
.
1. Алгоритм программы Polinom
|
Рис.1 Схема алгоритма подпрограммы Swap |
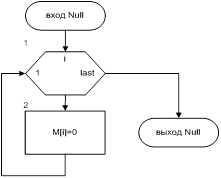
Рис.2 Схема алгоритма подпрограммы Null |
|
Рис.3 Схема алгоритма подпрограммы Rise |
Рис.4 Схема алгоритма подпрограммы Calculat |
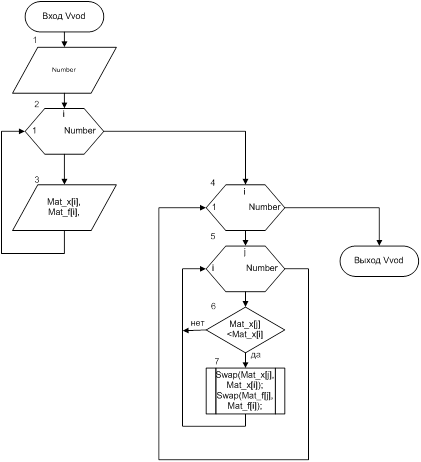
Рис.5 Схема алгоритма подпрограммы Vvod

Рис.6 Схема алгоритма программы Print_Polinom

Рис.7 Схема алгоритма подпрограммы Div_Res

Рис.8 Схема алгоритма программы Nuton

Рис.9 Схема алгоритма подпрограммы Recover

Рис.10 Блок-схема программы Polinom
Похожие работы
... в Украине, бывшем Советском Союзе и за рубежом научная школа теоретического программирования. В 2001-м году ее не стало... Но не только в научном плане велика роль женщин в развитии вычислительной техники. Со временем образуется огромное количество различных фирм по разработке и продаже программного и аппаратного обеспечения. Следовательно, разыгрываются человеческие трагедии капиталистического ...
... управляемы. Пользователь сумеет голосом подавать машине команды. Предполагается, что XXI век будет веком наибольшего использования достижений информатики в экономике, политике, науке, образовании, медицине, быту, военном деле. Главной тенденцией развития вычислительной техники в настоящее время является дальнейшее расширение сфер внедрения ЭВМ и, как следствие, переход от отдельных машин к их ...
... удивили меня…, хоть речь идёт обо мне самой. Они действительно написаны прекрасным стилем, который превосходит стиль самого очерка" /2/. 2.3. Рождение первенца и критическое перенапряжение Августа Ада Лавлейс работает с большим напряжением. В письмах к Бэббиджу она неоднократно жалуется на утомление, болезни, плохое самочувствие. Наконец, 6 августа Бэббидж отсылает Аде свои последние замечания ...
... № темы Наименование Темы Объем, час. в том числе, лекции, час. лабораторные работы, час. 1 2 3 4 5 6 7 8 1 семестр Введение в информатику и вычислительную технику Основы устройства и функционирования ЭВМ Операционная система Windows Современная вычислительная техника Программные ...



0 комментариев