Навигация
Дослідження чисельних методів інтегрування
Зміст
Вступ
1. Теоретичні відомості
2. Алгоритми методів
3. Опис програми
3.1 Вибір інструментальних засобів
3.2 Вхідні та вихідні дані
3.3 Структура програми
3.4 Інструкція користувачеві
4. Аналіз результатів розрахунку
Висновки
Література
Додатки
Вступ
Сучасний світ неможливо уявити без використання комп’ютерних технологій. Зараз комп’ютер використовується у багатьох сферах людського життя, але на початку свого розвитку ЕОМ створювалась для складних інженерних розрахунків. Зараз обчислення залишаються одним із основних видів застосування ЕОМ. Хоча комп’ютер дуже швидко виконує прості арифметичні дії, без спеціальних програм він не в змозі проводити складні обчислення. Тому постає задача алгоритмізувати поставлене завдання, тобто перевести його в зрозумілу для ЕОМ форму.
В багатьох задачах, що пов’язані з аналізом, ідентифікацією, оцінкою якості різних засобів та систем автоматики та управління, виникає необхідність обчислення певних інтегралів.
1. Теоретичні відомості
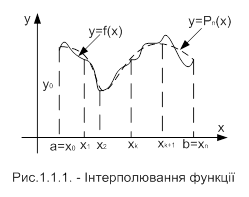
Визначений інтеграл – чисельно рівний площі, обмеженою частиною графіка функції y = f(x), віссю Ох і ординатами f(a) і f(b). Якщо крива перетинає вісь Ох один або декілька разів всередині інтервалу, то інтеграл чисельно рівний алгебраїчній сумі площ, що знаходяться по кожну сторону вісі Ох[6].
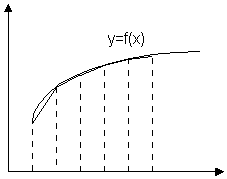
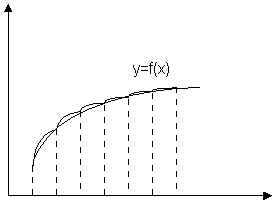
Чисельне інтегрування - являє собою стійкий процес і в протиставлення чисельному диференціюванню зменшує дію похибок у початкових даних на кінцевий результат. В основу чисельного інтегрування покладено наближене обчислення площини під кривою, яка описується підінтегральною функцією інтеграла:

Визначений інтеграл - являє собою площину, обмежену кривою f(x), віссю Х та прямими x=a; x=b[6].
Класифікація методів рішення поставленої задачі
Інженеру часто приходиться обчислювати визначений інтеграл чисельними методами. Це буває у тих випадках, коли або не вдається виразити інтеграл у замкненій формі, або вона настільки складна, що простіше скористатися чисельним інтегруванням.
Отже основною задачею є обчислення інтегралу виду:

де a і b - нижня та верхня межа інтегрування; f(x) - неперервна функція, відносно якої шукають інтеграл, на відрізку [a,b].
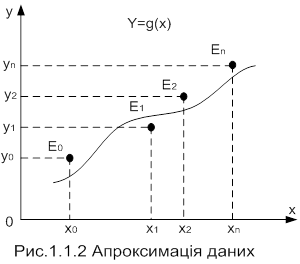
Суть більшості методів обчислення визначених інтегралів заключається в заміні підінтегральної функції f(x) апроксимуючою функцією f(х), для якої можна легко записати первісну в елементарних функціях, тобто

де S - наближене значення інтеграла; R - похибка обчислення інтеграла[2].
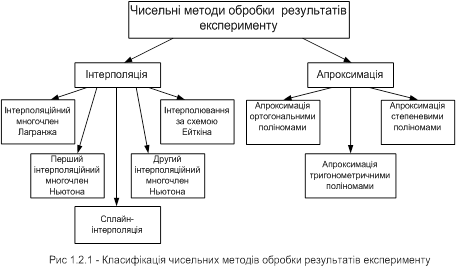
Методи чисельного інтегрування, що найбільш часто використовуються на практиці можна згрупувати в залежності від способу апроксимації підінтегральної функції. Дамо коротку характеристику груп найбільш розповсюджених методів.
Методи Ньютона-Котеса засновані на поліноміальній апроксимації підінтегральної функції. Методи цього класу відрізняються один від одного степенем використовуваного полінома, від якого залежить кількість вузлів, де необхідно обчислити функцію f(x). Алгоритми методів прості і легко піддаються програмній реалізації[1].
Сплайнові методи базуються на апроксимації підінтегральної функції сплайнами, що являють собою кусочний поліном. Методи розрізняють по типу вибраних сплайнів. Такі методи є сенс використовувати в задачах, де алгоритми сплайнової апроксимації застосовуються для обробки даних.
В методах найвищої алгебраїчної точності (методи Гаусса-Кристоффеля та інші) використовують не рівновіддалені вузли, розташовані по алгоритму, що забезпечує мінімальну похибку інтегрування для найбільш складних функцій при заданій кількості вузлів. Методи розрізняються способами вибору вузлів і широко використовуються для інтегрування, в тому числі вони можуть бути застосовані і для невласних інтегралів[3].
В методах Монте-Карло вузли вибираються за допомогою датчика випадкових чисел, відповідь носить ймовірний характер. Методи виявляються ефективними при обчисленні великої кратності.
2. Алгоритми методів
Для обчислення інтегралу за формулою Сімпсона потрібно спочатку розбити проміжок інтегрування x є (a,b) на рівні інтервали величиною h (крок інтегрування), потім знаходять вузли інтерполяції xi за формулою
xi=xi-1+h або xi=x0+ih=a+ih,
після чого підставляють отримані значення у формулу (3). В кінці оцінюють похибку. У додатку А приведено алгоритм методу Сімпсона.
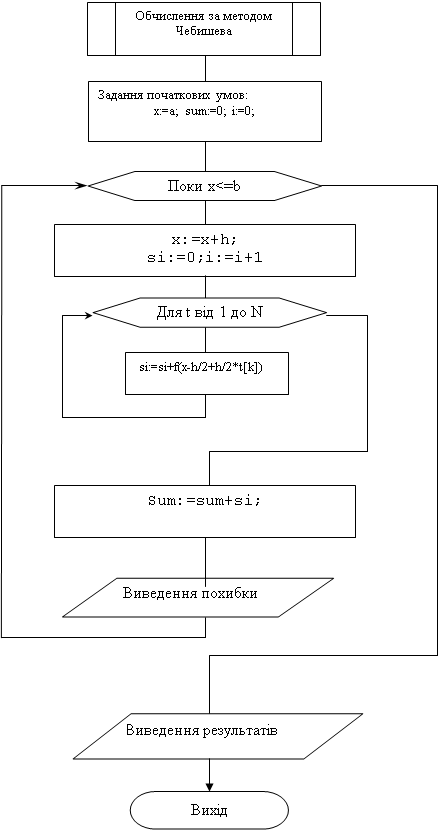
Для обчислення значення інтегралу методом Чебишева обирають порядок методу n і знаходять значення ti. Після цього розбивають інтервал інтегрування на k проміжків і знаходять значення інтегралу для кожного проміжку (j=1,…,k), після чого сумують отримані значення
|
|
Значення абсцис xi всередині кожного інтервалу знаходять за формулою
xi=(aj+1+aj)/2+ti(aj+1-aj)/2,
де aj=a+ih, a0=a, ak=b.
Ij знаходять за формулою (1.5). В кінці оцінюють похибку. Алгоритм методу Чебишева приведено у додатку А.
3. Опис програми
3.1 Вибір інструментальних засобів
Для написання програми, яка обчислює інтеграли заданими методами, було обрано компілятор Тurbo C++. Даний компілятор був обраний тому, що мова програмування C++ дуже проста і в той же час сам компілятор являється потужною сучасною системою програмування. Найважливішим аргументом для вибору даного компілятора, є тип дійсних чисел extended, який має дуже високу точність (до 19 цифри), якої немає в жодному іншому широковживаному компіляторі. Так як різниця між деякими числами, отриманими в результаті роботи програми, дуже мала і іноді помітна починаючи з дев’ятого знаку, то стає очевидним що потрібна точність саме такого порядку.
Похожие работы
... 2001): 2.68069545714219 Крок: 0.2 Інтеграл Чебишева 5-го порядку: 2.68069545714209 Загальна похибка: 0,00000000010 Точне розв’язання (Mathcad 2001): 2.68069545714219 Крок: 0.1 Висновки В даній курсовій роботі було проведене дослідження чисельних методів вирішення визначеного інтегралу виду I=, по методу Чебишева. Алгоритм методу є досить простим. Для його реалізації потрібно мати ...
... функцію задано аналітичнo, але її вираз досить складний і незручний для виконання різних математичних операцій (диференціювання, інтегрування тощо). 2 Розробка алгоритмів моделювання зміни температури термопари за допомогою чисельних методів на ЕОМ 2.1 Планування вхідних та вихідних даних Для розв’язання поставленої задачі потрібні певні вхідні данні, на основі яких будуть проводитись ...
... випадків, аварій, а з цим і простоїв на підприємстві, укріпити та створити культуру трудової діяльності. Виконання та розробка дипломного проекту “ Розробка дослідження системи керування електроприводом змінного струму дизель-потягу з використанням нейронних мереж ” відбувається за допомогою комп'ютера, тому питання охорони праці розглядаються щодо забезпечення здорових і безпечних умов роботи ...
... характеристика програми . Порядок підготовки вихідних даних для виконання розрахунку на ЕОМ. Схеми механічних систем та розрахункові дані до них. Перелік літератури. Вступ. Друга частина розрахункової роботи по дослідженню коливань системи з одним ступенем вільності включає задачу про дослідження малих вимушених коливань системи тіл з пружними елементами (пружинами) при дії на ...



0 комментариев