Навигация
Завдання лінійного програмування
Зміст
Вступ
1. Двовимірне завдання лінійного програмування
2. Графічний метод рішення3. Приклад 1
4. Табличний симплекс-метод5. Приклад 2
Література
Вступ
Тема контрольної роботи «Завдання лінійного програмування».
Мета виконання роботи: навчитися формалізувати та вирішувати двовимірні завдання лінійного програмування, а саме:
- двовимірне завдання лінійного програмування;
- методи рішення.
Моделі прийняття оптимальних рішень можна класифікувати як завдання мінімізації (максимізації) критерію ефективності, компоненти якого задовольняють системі обмежень (рівностей й/або) нерівностей.
Їх можна розділити на:
- прийняття рішень в умовах визначеності - вихідні дані - детерміновані;
- прийняття рішень в умовах невизначеності - вихідні дані - випадкові величини.
А за критерієм ефективності:
- одноцільове прийняття рішень (один критерій ефективності);
- багатоцільове прийняття рішень (декілька критеріїв ефективності).
Найбільш розроблений і широко використовується на практиці апарат одноцільового прийняття рішень в умовах визначеності, що одержав назву математичного програмування. У цьому "детермінованому" випадку, коли всі умови операції відомі заздалегідь тоді, зворотнє завдання буде містити у собі критерій ефективності й деякі відомі заздалегідь фактори (обмеження) що дозволяють вибрати множину припустимих рішень.
У широкому класі технічних завдань показник якості виражають лінійно через параметри проектованої системи, а умови, яким повинні задовольняти шукані параметри, записують у вигляді лінійних рівностей і нерівностей. Оптимізація подібних лінійних математичних моделей становить предмет лінійного програмування. Крім того, у багатьох нелінійних моделей через складність обчислювального процесу пошуку точного рішення використовують наближені методи, сутність яких складається у зведенні вихідних моделей до їхніх кусочно-лінійних аналогів, що дозволяють застосовувати методи лінійного програмування
1. Двовимірне завдання лінійного програмування
Двовимірне завдання лінійного програмування - завдання лінійного програмування, кількість змінних якої дорівнює 2.
Змінні прийнято позначати x1 й x2. Розглянуте раніше завдання лінійного програмування є двовимірним.
У загальному виді двовимірне завдання лінійного програмування можна представити в наступним образом.
Визначити значення змінних x1 та x2, при яких лінійна цільова функція F досягає максимуму (мінімуму)
F=з1x1+з2x2 → max (min) (1.1)
при обмеженнях на змінні:
 (1.2)
(1.2)
Серед обмежень можуть одночасно зустрічатися знаки >= , <= й =.
Коефіцієнти aij, bi, cj, i=1..m, j =1,2 будь-які дійсні числа (можливо й 0).
2. Графічний метод рішення
Двовимірні завдання лінійного програмування звичайно вирішуються графічно.
Алгоритм рішення задачи двумірного лінійного програмування графічним методом:
1. Будуємо область припустимих рішень функції F.
Для цьго в обмеженнях змінюємо знак нерівності на знаки рівняння і будуємо прямі. Далі визначаємо ті полуплощини, які відповідають обмеженням та отримуємо область припустимих значень, яка знаходиться на перетинанні всіх полуплощин.
2. Будуємо пряму рівня.
Для цьго обираємо будь яку точку М, яка належить до області припустимих рішень функції F, та підставивиши координати цієї точки в функцію, отримуємо пряму рівня. Далі від обраної точки М відкладуємо вектор а, координаті якого – це коефіціенти при цільвій функції F.
3. Максимізуємо (мінімізуємо) цільову функцію F.
Для максимізації (мінімізації) цільової функції F пересуваємо пряму рівня у напрямку, (в протилежному напрямку відносно) вектора а до перетинання з граничною точкою області припустимих рішень. Отримана точка є оптимальним рішенням, в якому функція досягає свого максимуму (мінімуму). Знаходимо координати цієї точки та підставляємо їх в функцію F.
3. Приклад 1
Вирішимо отримане двовимірне завдання лінійного програмування графічно:

Рішення:
Побудова області припустимих рішень цільової функції F
Побудуємо прямокутну систему координат, де вісь ОX позначимо за x1, а OY - за x2.
Тому що, відповідно до умови (3) x1 й x2 ненегативні, то можна обмежиться розгляданням першого квадранта.
Розглянемо перше обмеження:
3x1+4x2<=1700 (1)
Замінимо в даному обмеженні знак нерівності знаком рівняння й побудуємо пряму.
3x1+4x2=1700 (1')
Для цього знайдемо дві крапки, що належать даній прямій.
Нехай, наприклад, x1=0, тоді підставивши 0 в (1') одержимо 4x2=1700 або x2=425.
(0: 425) - координати першої крапки, що належить прямій.
Нехай x2=0, те 3x1=1700, отже, x1=567.
(567:0) - координати другої крапки, що належить прямій.
Відзначимо ці крапки на числових осях.
Аналогічно, для другого обмеження:
2x1+5x2<=1600 (2)
2x1+5x2=1600 (2')
При x1=0, x2=320 (0; 320)
При x2=0, x1=800 (800; 0)
Побудуємо дані прямі (на малюнку вони відповідно позначені (1') і (2')).
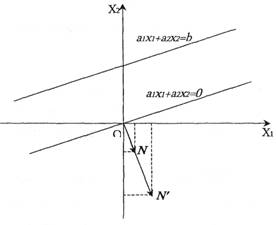
Тепер знайдемо на кресленні такі напівплощини, які відповідають нерівностям (1) і (2).
Пряма (1') 3x1+4x2=1700 ділить координатну площину на дві напівплощини. Одна напівплощина розташована вище прямої, друга нижче. Щоб знайти ту напівплощину, що відповідає нерівності (1), необхідно взяти будь яку крапку яка належить одній з напівплощин і підставити її координати в нерівність. Якщо нерівність буде вірною, то дана напівплощина є шуканою.
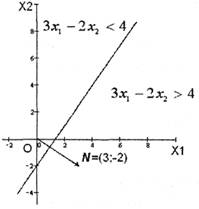
Наприклад, візьмемо крапку з координатами (0; 0) і підставимо її координати в нерівність (1) 3x1+4x2<=1700 або 0+0<=1700.
Виходить 0<=1700 - дана нерівність є вірною, отже, нерівності (1) задовольняє напівплощина, що лежить нижче прямої (1').
Аналогічно, надійдемо для нерівності (2) 2x1+5x2<=1600. Візьмемо крапку з координатами (0; 0).
Виходить 0<=1600 - дана нерівність вірна. Нерівності (2) задовольняє напівплощина, розташована нижче прямій (2').
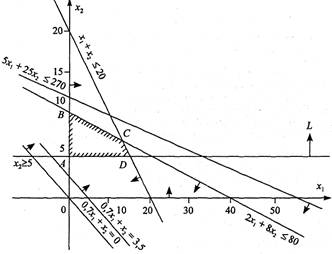
Стрілки на кожній границі, з якої сторони прямої виконані обмеження. З огляду на, те що x1 й x2 є ненегативними, одержуємо, що чотирикутник ОАВС є областю, що містить крапки, для яких виконані умови, укладені у фігурні дужки.
Точки, що лежать усередині й на границі цієї області є припустимими рішеннями, але нам потрібні, тільки ті, при яких функція F буде приймати максимальне значення.
Побудова прямої рівня.
Візьмемо довільну крапку, що належить області припустимих рішень - чотирикутнику ОАВС, наприклад, крапку М с координатами (100; 100). Підставимо координати крапки М у функцію F.
F(100; 100)=2*100+4*100=600.
Пряма рівня буде мати такий вигляд: 2x1+4x2=600
Побудуємо отриману пряму. Для цього необхідно знайти координати двох довільних крапок цієї прямої. Одна крапка в нас уже є - це крапка М(100; 100). Знайдемо ще одну крапку. Нехай x2=0, тоді x1=300. Отже, координати додаткової крапки (300; 0). Відзначимо отримані крапки й побудує пряму рівня (на малюнку 1 вона позначена (3')).
Значення функції F будуть зростати в міру того, як пряма рівня віддаляється від початку координат у позитивному квадранті. Напрямок зростання функції F буде збігатися з вектором, координати якого є коефіцієнтами при змінних x1 й x2 функції F. На малюнку - це вектор a{2; 4}, відкладений від крапки М.
Треба звернути увагу, що вектор a, який визначає напрямок зростання функції F, завжди буде перпендикулярний прямій рівня.
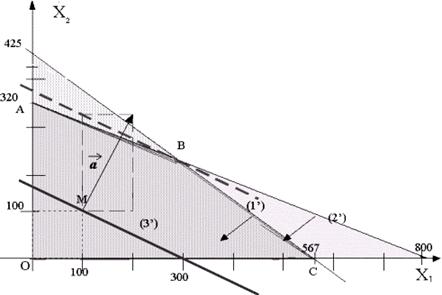
Рис.1.Максимізація цільової функції F.
Для знаходження крапки, у якій функція F досягне свого максимального значення, необхідно переміщати пряму рівня по напрямку вектора a до перетинання цієї прямої із граничною крапкою області припустимих рішень. На нашому малюнку - це крапка В.
Знайдемо координати крапки B.
Дана крапка розташована на перетинанні двох прямих (1') і (2'), тому, щоб знайти її координати необхідно вирішити наступну систему рівнянь:
![]()
Із другого рівняння виразимо x1

І підставимо отримане значення в перше рівняння.

(300; 200) - крапка, що відповідає оптимальному рішенню завдання, отже, максимальне значення становить 2*300+4*200=1400 умовних одиниць. Виходить, щоб дістати максимальний прибуток, необхідно випускати в тиждень триста одиниць моделі А и двісті одиниць моделі В.
Похожие работы
... , а при більшому числі змінних - взагалі неможливим. Незважаючи на це, розгляд графічного методу дасть змогу зробити висновки, що послужать основою для розробки загального методу розв’язання задач лінійного програмування[2]. Перший крок при використанні графічного методу полягає в поданні області допустимих розв’язків, у якій водночас задовольняються всі обмеження моделі. Нехай шукана область ( ...
... стратегія володіє тим властивістю, що стосовно будь-якого первісного стану після деякого етапу рішення сукупність наступних рішень повинна становити оптимальну стратегію. Цей принцип оптимальності лежить в основі всієї концепції динамічного програмування. Саме завдяки йому вдається при наступних переходах випробовувати не всі можливі варіанти, а лише оптимальні виходи. Рекурентні співвідношення ...
... розвиток як математична теорія лінійного і нелінійного програмування, так і додаток її методів до дослідження різних економічних проблем. У 1949 р. американським математиком Дж. Данцигом (GB Dantzig) був опублікований симплекс-метод - основний метод рішення задач лінійного програмування. Термін «лінійне програмування» вперше з'явився в 1951 р. в роботах Дж. Данцига і Т. Купманса. При всьому ...
... зумовлюється метою, якої хочуть досягти даною геометричною інтерпретацією та особливостями структури самої задачі, в тому числі й формою її представлення. Для геометричної інтерпретації візьмемо основну задачу лінійного програмування у другій стандартній формі. Для наочності розглянемо найпростіший випадок, коли в системі обмежень (26) і цільовій функції (25) є лише дві змінних, Розглянемо розв' ...

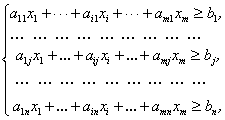
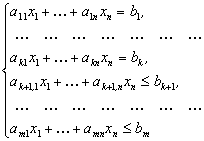
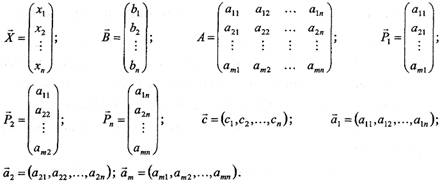
0 комментариев