Навигация
Упорядочить данные по убыванию (или по возрастанию) той независимой переменной, относительно которой есть подозрение на гетероскедастичность
1. Упорядочить данные по убыванию (или по возрастанию) той независимой переменной, относительно которой есть подозрение на гетероскедастичность.
2. Исключить ![]() средних (в этом упорядочении) наблюдений (
средних (в этом упорядочении) наблюдений (![]() , где
, где ![]() – общее количество наблюдений).
– общее количество наблюдений).
3. Провести две независимых регрессии первых  наблюдений и последних
наблюдений и последних  наблюдений и найти, соответственно,
наблюдений и найти, соответственно, ![]() и
и ![]() . Из
. Из ![]() и
и ![]() выбираем большую и меньшую величины, соответственно,
выбираем большую и меньшую величины, соответственно, ![]() и
и ![]() .
.
4. Составить статистику  и найти по распределению Фишера
и найти по распределению Фишера  , где
, где ![]() – число объясняющих переменных модели.
– число объясняющих переменных модели.
5. Если ![]() , то гипотеза
, то гипотеза ![]() отвергается, т.е. модель гетероскедастична, а если
отвергается, т.е. модель гетероскедастична, а если ![]() , то гипотеза
, то гипотеза ![]() принимается, т.е. модель гомоскедастична.
принимается, т.е. модель гомоскедастична.
Тест Бреуша – Пагана (Breusch - Pagan)
Этот тест применяется в тех случаях, когда предполагается, что дисперсии ![]() зависят от некоторых дополнительных переменных. Пусть
зависят от некоторых дополнительных переменных. Пусть ![]() ,
, ![]() . Тест состоит в следующем:
. Тест состоит в следующем:
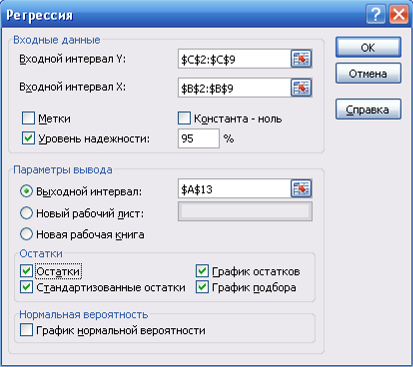
1. Провести обычную регрессию и получить ![]() . (Для этого в диалоговом окне Регрессия установить флажок на функцию Остатки)
. (Для этого в диалоговом окне Регрессия установить флажок на функцию Остатки)
2. Построить оценку ![]() .
.
3. Провести регрессию  и найти для нее объясненную часть вариации
и найти для нее объясненную часть вариации ![]() .
.
4. Построить статистику ![]() .
.
5. Если ![]() (где p – число переменных, от которых зависит
(где p – число переменных, от которых зависит ![]() ), то имеет место гетероскедастичность.
), то имеет место гетероскедастичность.
Если ![]() , то - гомоскедастичность.
, то - гомоскедастичность.
![]() - критическая точка распределения
- критическая точка распределения ![]() (хи-квадрат) при выбранном уровне значимости
(хи-квадрат) при выбранном уровне значимости ![]() , для нахождения которой выполнить следующую последовательность действий: fx
, для нахождения которой выполнить следующую последовательность действий: fx![]() Статистические
Статистические![]() ХИ2ОБР
ХИ2ОБР
![]()
Тест Дарбина – Уотсона (Darbin-Watson) на наличие автокорреляции
Этот тест используется для обнаружения автокорреляции первого порядка, т.е. проверяется некоррелированность не любых, а только соседних величин ![]() . Соседними обычно считаются соседние во времени (при рассмотрении временных рядов) или по возрастанию объясняющей переменной
. Соседними обычно считаются соседние во времени (при рассмотрении временных рядов) или по возрастанию объясняющей переменной ![]() значения
значения ![]() .
.
![]()
Гипотеза ![]() (автокорреляция отсутствует).
(автокорреляция отсутствует).
Общая схема критерия Дарбина – Уотсона следующая:
1. По эмпирическим данным построить уравнение регрессии по МНК и определить значения отклонений ![]() для каждого наблюдения t (t = 1, 2, …, n).
для каждого наблюдения t (t = 1, 2, …, n).
2. Рассчитать статистику DW:

3. По таблице критических точек распределения Дарбина –Уотсона для заданного уровня значимости ![]() , числа наблюдений
, числа наблюдений ![]() и количества объясняющих переменных
и количества объясняющих переменных ![]() определить два значения:
определить два значения: ![]() - нижняя граница и
- нижняя граница и ![]() - верхняя граница (таблица 2).
- верхняя граница (таблица 2).
Полный вариант таблицы приведен в разделе Математико-статистические таблицы (Таблица 5. Значения dH и dB критерия Дарбина—Уотсона на уровне значимости = 0,05 (n — число наблюдений, р — число объясняющих переменных). множественный корреляция регрессия
Таблица 2.
| Статистика Дарбина – Уотсона, уровень значимости 0,05 | |||||||||||
|
| 1 | 2 | 3 | 4 | 5 | |||||
|
|
|
|
|
|
|
|
|
|
|
|
| 20 | 1,20 | 1,41 | 1,1 | 1,54 | 1,00 | 1,67 | 0,90 | 1,83 | 0,79 | 1,99 |
| 21 | 1,22 | 1,42 | 1,13 | 1,54 | 1,03 | 1,66 | 0,93 | 1,81 | 0,83 | 1,96 |
| 22 | 1,24 | 1,43 | 1,15 | 1,54 | 1,05 | 1,66 | 0,96 | 1,80 | 0,86 | 1,94 |
| 23 | 1,26 | 1,44 | 1,17 | 1,54 | 1,08 | 1,66 | 0,99 | 1,79 | 0,90 | 1,92 |
| 24 | 1,27 | 1,45 | 1,19 | 1,55 | 1,10 | 1,66 | 1,01 | 1,78 | 0,93 | 1,90 |
| 25 | 1,29 | 1,45 | 1,21 | 1,55 | 1,12 | 1,66 | 1,04 | 1,77 | 0,95 | 1,89 |
4. Сделать выводы по правилу:
![]() - существует положительная автокорреляция (
- существует положительная автокорреляция (![]() ),
), ![]() отвергается;
отвергается;
![]() - вывод о наличии автокорреляции не определен;
- вывод о наличии автокорреляции не определен;
![]() - автокорреляция отсутствует,
- автокорреляция отсутствует, ![]() принимается;
принимается;
![]() - вывод о наличии автокорреляции не определен;
- вывод о наличии автокорреляции не определен;
![]() - существует отрицательная автокорреляция (
- существует отрицательная автокорреляция (![]() ),
), ![]() отвергается.
отвергается.
Похожие работы
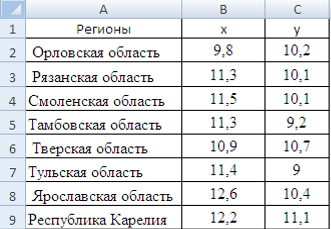
... и детерминации и F-критериев Фишера наибольшие. 3. Множественная регрессия Цель работы – овладеть методикой построения линейных моделей множественной регрессии, оценки их существенности и значимости, расчетом показателей множественной регрессии и корреляции. Постановка задачи. По данным изучаемых регионов (таблица 1) изучить зависимость общего коэффициента рождаемости () от уровня бедности ...
... 7,33 1965 81,0 7,52 1966 83,0 7,62 1967 85,4 7,72 1968 85,9 7,89 1969 85,9 7,98 1970 87,0 8,03 1971 90,2 8,21 1972 92,6 8,53 1973 95,0 8,55 1974 93,3 8,28 1975 95,5 8,12 Найдем параметры линейного уравнения множественной регрессии и значения остатков. Дополним таблицу данных столбцами "", "Квадрат разности остатков " и "Квадрат остатка " и заполним их. Таблица ...
... t-критерий Стъюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Но о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки: Оценка значимости коэффициентов чистой регрессии с помощью /-критерия ...
... взяты за 2003 год. Данные взяты из статистического сборника Регионы России Социально-экономические показатели. 2003. Федеральная служба государственной статистики Построение модели множественной регрессии Расчет параметров Рассчитаем необходимые параметры: Признак Ср. знач. СКО Характеристики тесноты связи βi bi Коэф-ты частной корр. F-критерий фактический ...

0 комментариев