Навигация
4 ПРОГРАМНА РЕАЛІЗАЦІЯ
4.1 Опис алгоритму та структури програми
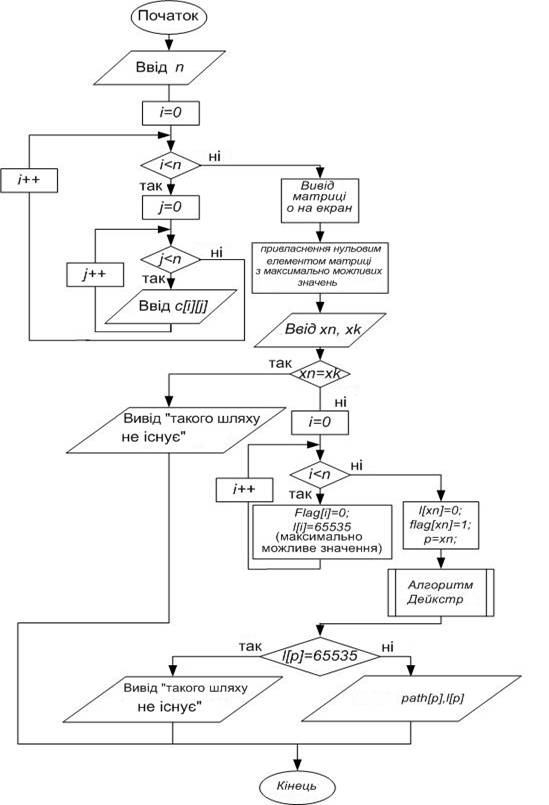
Рис.4.1.1
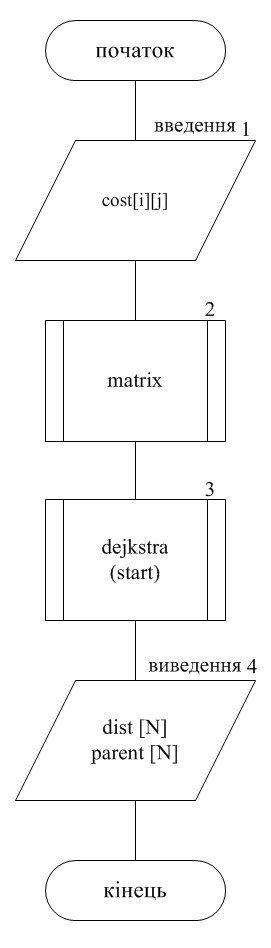
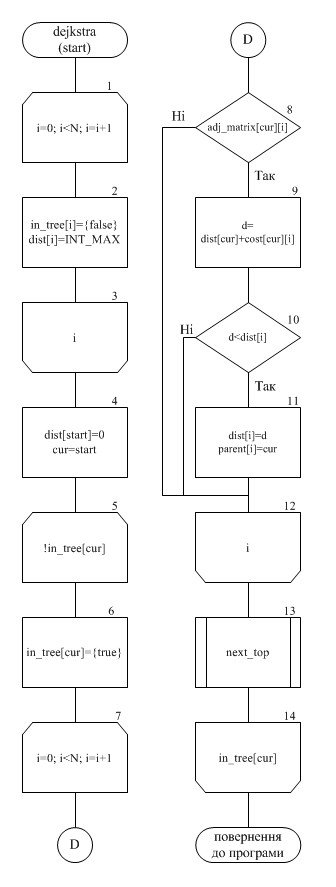
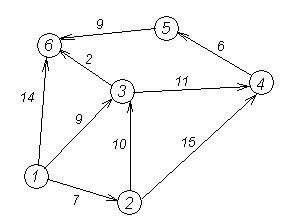
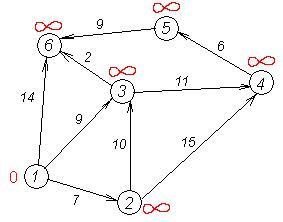
Програма виводить мінімальний шлях між двома зазначеними вершинами у графі і його довжину. При запуску програми на екран виводиться запит про введення ваг ребер досліджуваного графа. Дані, введені користувачем, відображаються у вигляді матриці суміжності, в якій не існуючі ребра позначаються нулями. Після зазначеним ребрах присвоюється значення 65535, яке приймається за нескінченність. Наступним етапом виконання програми є запит про введення номерів вершин, між якими необхідно дізнатися шлях. У випадку, якщо початкова та кінцева вершини співпадають, з'являється повідомлення і робота програми завершується. В іншому випадку виконується безпосередньо алгоритм Дейкстри, схема якого наведена у додатку В. Результатом програми є вивід на екран вершин, через які проходить мінімальний шлях, а також виведення довжини маршруту. Якщо шляху між заданими точками не існує - виводиться відповідне повідомлення.
4.2 Опис використаних програмних засобів
Таблица 4.2.1–Опис змінних
| Змінна | Тип | Опис |
| n | int | Кількість точок (вершин) графа |
| i,j | int | Лічильники |
| p | int | Номер найкоротшого шляху і найменшої довжини шляху |
| xn | int | Номер початкової точки (вершини) |
| xk | int | Номер кінцевої точки (вершини) |
| flag[11] | int | Масив, i-й елемент якого має значення 0, коли i-й шлях і відстань тимчасові, і приймає значення 1, коли i-й шлях і відстань стають постійними |
| c[11][11] | word (unsigned int) | Масив i-j елемент якого містить відстань між i-й і j-й крапками (вершинами)Зауваження: 1. с[i][i]=¥ 2. c[i][j]=c[j][i] |
| s[80] | char | Рядкова змінна, яка містить проміжні значення шляху |
| path[80][11] | char | Масив рядків, який містить шляхуЗауваження:Після проходження обробки за алгоритмом Дейкстри p-й елемент масиву містить найкоротший шлях. |
| l[11] | word (unsigned int) | Масив, який містить довжини шляхів (path)Зауваження:Після проходження обробки за алгоритмом Дейкстри p-й елемент масиву містить довжину найкоротшого шляху. |
Крім стандартних функцій з бібліотек iostream.h, string.h, stdio.h, conio.h були використані також наступні функції.• word minim (word x, word y) - функція, яка повертає мінімальне з x і y.
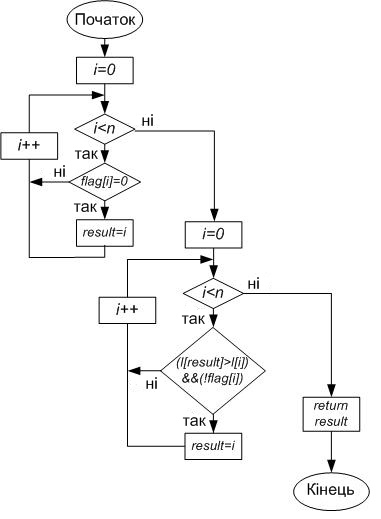
Рис.4.2.1
• int min (int n) - функція, яка повертає номер елемента масиву l [i] мінімальної «невідмічений» довжиною шляху (flag [i] = 0).

Рис.4.2.2
5. ІНСТРУКЦІЯ КОРИСТУВАЧА
При запуску програми на екрані з'явиться вікно з інструкціями. Виконуйте ці інструкції, а саме: 1. Введіть кількість вершин досліджуваного графа. 2. Введіть ваги ребер (позитивне число). У програмі відстані від хi до xi+1 та xi+1 до хi вважаються рівними, а відстані від хi до хi - не існуючими. Якщо ребра між зазначеними вершинами не існує, введіть 0 (нуль). На екран виводиться матриця суміжності, що відображає введену інформацію. 3. Введіть номер вершини, від якої починається шуканий шлях. 4. Введіть номер вершини, у якій шлях закінчується. 5. Щоб завершити роботу програми після отримання результату натисніть Enter.
ВИСНОВОК
Таким чином, в процесі створення даного проекту розроблена програма, що реалізує алгоритм Дейкстри в Microsoft Visual C + + 6.0. Її недоліком є примітивний користувальницький інтерфейс. Це пов'язано з тим, що програма працює в консольному режимі, не додає до складності мови складність програмного віконного інтерфейсу. Також були поглиблені знання, отримані в процесі виконання лабораторних робіт з предмету «Програмування».
ПЕРЕЛІК ПОСИЛАННЯ
1. Бондарєв В.М. Програмування на С + + .- Х: «Компанія СМІТ», 2004
2. Страуструп Бьярн Мова програмування С + + (2 рік) .- «К: ДіаСофт», 1993
3. Хаханов В.І., Чумаченко С.В. Дискретна математика (теоретичне І практичне Зміст курсу) .- Кафедра АПОТ, 2002
4. Алгоритм Дейкстри
5. Конспект лекцій.
Додаток А
Текст програми
#include<iostream.h>
#include<string.h>
#include<stdio.h>
#include<stdlib.h>
#include<conio.h>
#define word unsigned int
int i, j, n, p, xn, xk;
int flag[11];
word c[11][11], l[11];
char s[80], path[80][11];
int min(int n)
{
int i, result;
for(i=0;i<n;i++)
if(!(flag[i])) result=i;
for(i=0;i<n;i++)
if((l[result]>l[i])&&(!flag[i])) result=i;
return result;
}
word minim(word x, word y)
{
if(x<y) return x;
return y;
}
void main()
{
cout<<"Vvedit` kil`kist` tochok: ";
cin>>n;
for(i=0;i<n;i++)
for(j=0;j<n;j++) c[i][j]=0;
for(i=0;i<n;i++)
for(j=i+1;j<n;j++)
{
cout<<"Vvedit` vidstan` vid x"<<i+1<<" do x"<<j+1<<": ";
cin>>c[i][j];
}
cout<<" ";
for(i=0;i<n;i++) cout<<" X"<<i+1;
cout<<endl<<endl;
for(i=0;i<n;i++)
{
printf("X%d",i+1);
for(j=0;j<n;j++)
{
printf("%6d",c[i][j]);
c[j][i]=c[i][j];
}
printf("\n\n");
}
for(i=0;i<n;i++)
for(j=0;j<n;j++)
if(c[i][j]==0) c[i][j]=65535; //безкінечнність
cout<<"Vvedit` pochatkovi tochku: ";
cin>>xn;
cout<<"Vvedit` kincevi tochku: ";
cin>>xk;
xk--;
xn--;
if(xn==xk)
{
cout<<"Pochatkova i kinceva tochku spivpadayut`."<<endl;
getch();
return;
}
for(i=0;i<n;i++)
{
flag[i]=0;
l[i]=65535;
}
l[xn]=0;
flag[xn]=1;
p=xn;
itoa(xn+1,s,10);
for(i=1;i<=n;i++)
{
strcpy(path[i],"X");
strcat(path[i],s);
}
do
{
for(i=0;i<n;i++)
if((c[p][i]!=65535)&&(!flag[i])&&(i!=p))
{
if(l[i]>l[p]+c[p][i])
{
itoa(i+1,s,10);
strcpy(path[i+1],path[p+1]);
strcat(path[i+1],"-X");
strcat(path[i+1],s);
}
l[i]=minim(l[i],l[p]+c[p][i]);
}
p=min(n);
flag[p]=1;
}
while(p!=xk);
if(l[p]!=65535)
{
cout<<"Shljah: "<<path[p+1]<<endl;
cout<<"Dovjuna shljahy: "<<l[p]<<endl;
}
else
cout<<"takogo shljahy ne isnye!"<<endl;
getch();
}
Додаток Б
Результат
Додаток В
Схема програмної реалізації алгоритму Дейкстри

Похожие работы
... зноманітними типами транспортних засобів з урахуванням обмеження на обсяг робот, що можуть виконати транспортні засоби. РОЗДІЛ 3 МАТЕМАТИЧНА МОДЕЛЬ ТРАНСПОРТНОЇ СИСТЕМИ ПІДПРИЄМСТВА 3.1 Структура моделі У якості структурної моделі транспортної системи підприємства можна запропонувати схему, що складається з трьох рівнів. Необхідно відзначити, що з метою деякого спрощення задачі розгляда ...
... і певну кількість нових машин). Більшість дискретних і комбінаторних задач можна вирішити шляхом перебору. Проте перебірні методи мають експоненційну складність. Проблема: знайти метод вирішення експоненційних задач за поліноміальний час. 3.1 Планування в просторі станів. Основні поняття теорії графів Граф – сукупність вершин і дуг. Для комп’ютерного опису графу використовуються: матриця і ...
... графа рівно один раз. Означення.3.2 . Зв’язний граф називається напівгамільтоновим , якщо існує ланцюг , який проходить через кожну його вершину рівно один раз. Не дивлячись на подібність в означеннях ойлерових та гамільтонових графів, відповідно теорії для цих класів графів сильно відрізняються. До теорії гамільтонових графів відноситься і задача про бродячого тор-говця, або задача про комі ...
... оцінка складності алгоритму - О(n*log(n)). Даний алгоритм має сенс застосування лише на великих обсягах даних від 500-1000 елементів. Тільки в цьому випадку можна побачити виграш алгоритму в ефективності. Для менших обсягів даних він малопридатний. 3 Синтез машини Тьюрінга 3.1 Загальні відомості Машина Тьюрінга - це кінцевий автомат, забезпечений безкінченою стрічкою і читаючою/записуючою голівкою ...
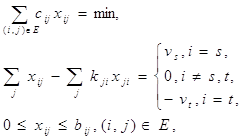
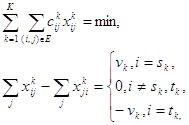


0 комментариев