Экономико - математическое моделиpование

ЗАДАЧА 1 Условие задачи.

Задана следующая экономическая ситуация. Завод выпускает изделия двух типов А и В. При этом используется сырье четырех видов. Расход сырья каждого вида на изготовление еденицы продукции и запасы сырья заданы в таблице

Изделия Сырье

1234

А2102

В3011

Запасы сырья 214610

Выпуск изделия А приносит 3 денежные еденицы, В - 2 денежные единицы.

Составить план производства, обеспечивающий максимальную прибыль

а) составьте матиматическую модель задачи;

б) поясните смысл целевой функции и ограничении

Решение:

а) Математическая модель

2x1+3x2 <=21

x1 <=4

x2+ <=6

2x1+ x2 <=10

x1 >=0

x2 >=0

б) Суммарный расход каждого вида сырья на весь выпуск не должен превышать заданного ограничения.

Валовая реализация (сумма объемов реализации по каждому виду продукции в денежном выражении) должна стремиться при заданных условиях к максиму

в) Решать будем симплекс методом преобразуем неравенства в равенства, для этого введем четыре дополнительные переменные

2x1+3x2+ x3 =21

x1 + x4 =4

x2 +x5 =6

2x1+x2+ x6 =10

f=3x1+2x2+0*x3+0*x4+0*x5+0*x6 -> max

перепишем в виде систем 0 уравнений

0= 21-(2x1+3x2+x3)

0= 4-( x1 + x4)

0= 6-( x2+ х5)

0=10-(2х1+х2+ х6)

f=0-(-3x1-2x2-0*x3-0*x4-0*x5-0*x6)

Система уравнений может быть записана в виде векторного равенства

0=В - (А1х1+А2х2+А3х3+А4х4+А5х5+А6х6)

В - свободные члены

А1…А6 коэффициенты при переменных х1…х6

Линейная форма имеет вид : f=c1x1+c2x2+c3x3+c4x4+c5x5+c6x6

Векторы А3,А4, А5,А6 составляют базис

Составляем первую симплекс таблицу

Базисный векторКоэф.лин. формы свектор св. член bb/a3 A12 A20 A30 A40 A50 A6

А302110,5231000

A4044100100

A5060010010

A60105210001

индексная строка fj-сj0-3-2

Решение: х1=0,х2=0,х3=21,х4=4,х5=6,х6=10

f=0

Так как в индексной строке есть отрицательные элементы -решение не является оптимальным.

A1 вводим в базис вместо вектора А4

Базисный векторКоэф.лин. формы свектор св. член bb/a3 A12 A20 A30 A40 A50 A6

A30134 1/3 0 3 1 -2 0 0

A1340 1 0 0 1 0 0

А5066 0 1 0 0 1 0

A6022 0 1 0 -2 0 1

индексная строка fj-сj0 -2 0 3 0 0

Решение:х1=4,х2=0,х3=13,х4=0,х5=6,х6=2

f=12

Так как в индексной строке есть отрицательные элементы -решение не является оптимальным.

A2 вводим в базис вместо вектора А6

Базисный векторКоэф.лин. формы свектор св. член bb/a8 A17 A26 A30 A40 A50 A6

A3071 3/4 0 0 1 4 0 -3

A1344 1 0 0 1 0 0

А5042 0 0 0 2 1 -1

A222-1 0 1 0 -2 0 1

индексная строка fj-сj0 0 0 -1 0 2

Решение:x1=4, x2=2; x3=7; x4=0;x5=4;x6=0

f=12

Так как в индексной строке есть отрицательные элементы -решение не является оптимальным.

A4 вводим в базис вместо вектора А3

Базисный векторКоэф.лин. формы свектор св. член bb/a8 A17 A26 A30 A40 A50 A6

A401 3/40 0 1/41 0 - 3/4

A132 1/41 0 - 1/40 0 3/4

А50 1/20 0 - 1/20 1 1/4

A225 1/20 1 1/20 0 -1 1/2

индексная строка fj-сj0 0 1/40 0 1 1/4

Решение:x1=2,25, x2=5,5; x3=0; x4=1 3/4;x5=1/2;x6=0

f=17,75

В индексной строке нет отрицательных элементов, следовательно дальнейшее увеличение значения линейной формы невозможно мы получили оптимальную программу

Максимальная прибыль достигается при изготовлении первого вида продукции 2,25 у.е., а второго 5,5 у.е.

Так как нам не было задано условие целочисленности, такие значения допустимы, например в качестве условных едениц - тысячи тонн.

ЗАДАЧА 2

Наити максимум функции F при заданных ограничениях

F = x1+2x2 ->max

3x1+x2 >=3(1)

3x1-x2 <=0(2)

x1-x2 >=3(3)

x1>=0(4)

x2>=0(5)

Решить графическим методом

Решение

1.Из условия знакоположительности - первой допустимой областью решения является первая четверть декартовой системы координат

2. Построим области допустимых значений, для этого построим линии для каждого из уравнений

3x1+x2 =3

3x1-x2 =0

x1-x2 =3

и линию для функции f

x1+2x2 =0

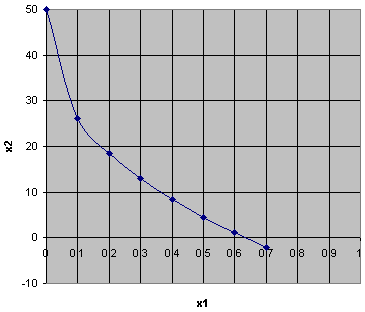
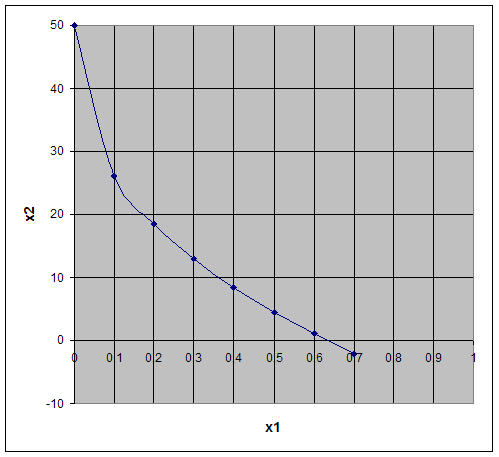
3. Наидем область допустимых значений

4. Как видно на графике области допустимых значений для ограничении (1),(2) и (3) не пересекаются, значит система не имеет допустимых решений. Ограничения противоречивы.

5.Для того чтобы система была решаема, она должна быть например

такойF = x1+2x2 ->max

3x1+x2 <=3

3x1-x2 <=0

x1-x2 <=3

x1>=0

x2>=0

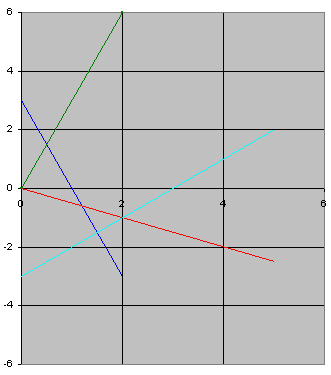
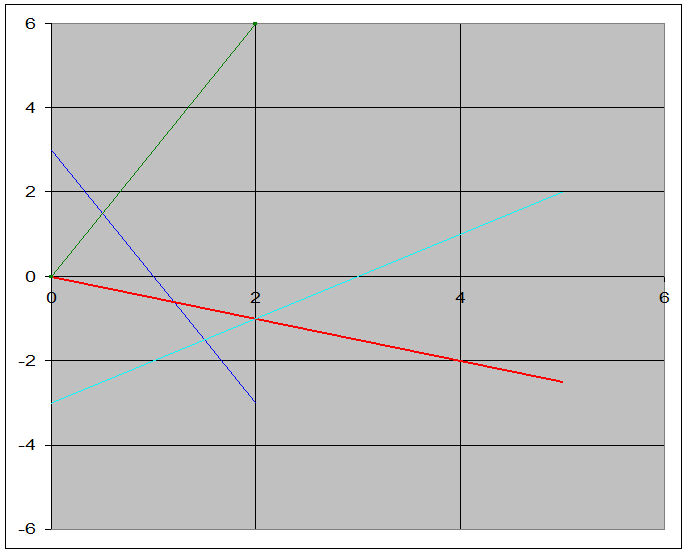
Тогда область допустимых решений - треугольник АВС

И функция F достигает максимума в точке С (0;3) и F=6

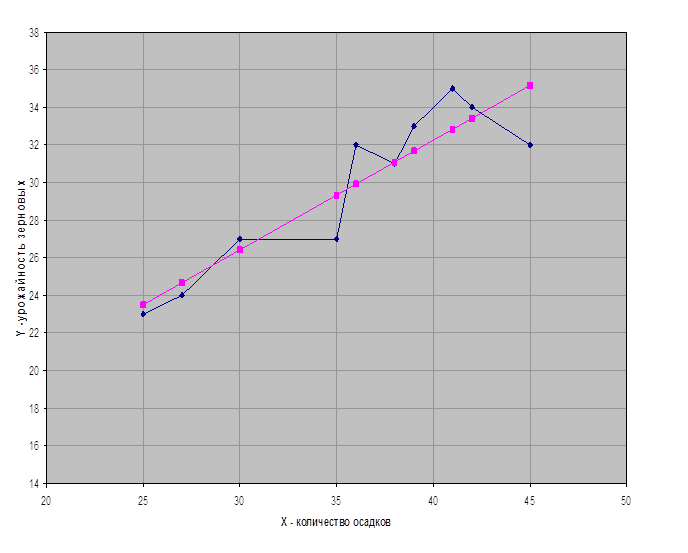
ЗАДАЧА 3

Имеются следующие данные об урожайности зерновых культур Y (в ц/га) количестве осадков Х1 (в см) выпавших в вегетационный период

i12345678910

Yi23242727323133353432

Xi25273035363839414245

Требуется :

а)Определить параметры уравнения регрессии;

б) определить коэффициент парной корреляции и проверить его статическую надежность

1. Количественные оценки связи между величинами случайного процесса устанавливает регрессионный анализ. Связи между переменными могут линейные и нелинейные. В простейшем случае значения Y выражаются в виде линейной зависимости :

Y =a + bX,

где a и b - коэффициенты регрессии.

Наиболее часто для расчетов коэффициентов применяют метод наименьших квадратов.