Навигация
3. Преобразование Уолша
Рассмотрим спектральное представление сигналов с использованием базиса Уолша. Аналогично с рядом Фурье ряд Уолша имеет вид:
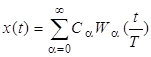 , (4)
, (4)
где спектр Уолша
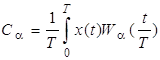 . (5)
. (5)
Для проверки правильности расчета спектральных коэффициентов может быть использовано равенство Парсеваля
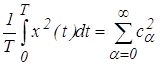 .
.
Если ограничиться N членами в разложении, то получим усеченный ряд Уолша:
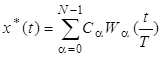 ,(6)
,(6)
где tÎ[0,T]; N=T/Dt; t = a Dtпри t® ¥a® ¥ , a - сдвиг по оси;
![]() wal(n,Q) после преобразования аргументов.
wal(n,Q) после преобразования аргументов.
Для практических расчетов можно использовать формулу:
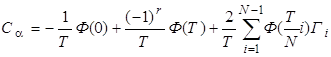 .
.
где: ![]() ; (7)
; (7)
r - ранг спектрального коэффициента с номером a (число двоичных разрядов числа a в которых имеются 1).
i - номер подынтервала определения функции x(t);
![]() . (8)
. (8)
При этом Гi принимает значение ±1 или 0 в зависимости от того меняет ли Wa(i/N) в точке i/N знак с "+" на "-",c "-" на " +" или знак не меняется.
Пример 1. Разложить функцию x(t) = at в ряд по упорядоченным по Пэли функциям Уолша при N=8, T=1, a=1.
Решение:Определим Ф(t):
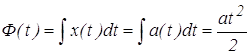 .
.
Определим спектральные коэффициенты с учетом функций Уолша упорядоченным по Пэли по формуле (7)
C0 = aT/2;
C1 = -aT/2 + 0 +0 + 0 +2(aT/4) + 0 + 0 + 0 = -aT/4;
C2 = -aT/2 + 0 + 4aT/64) + 0 - 16aT/64 + 0 +36aT/64 +0 =-aT/8;
C3 = aT/2 + 0 + 4aT/64) + 0 + 0 + 0 - 36aT/64 +0 = 0;
C4 =-aT/2 + aT/64 - 4aT/64 + 9aT/64 - 16aT/64 + 25aT/64 –
- 36aT/64 + 49aT/64 =-aT/16;
C5=C6=C7=0.![]()
Ряд Уолша - Пэли имеет вид:
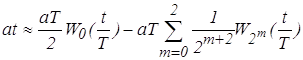 .
.
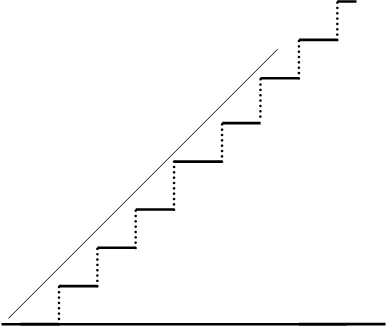
Аппроксимация функции x(t) = at при а=1 и t=1 полученным рядом приведена на рис. 3.
X

![]()
![]()
![]()
![]()
![]() 1
1
0 1 t
Рис . 3. Аппроксимация функции x(t)=at рядом Уолша – Пэли
4. Дискретное преобразование Уолша
Дискретное преобразование Уолша (ДПУ) производится при использовании дискретных функций Уолша Wa(i/N) Þ Wal(n, Q) и выполняется над решетчатыми сигналами x(i) , при этом число отсчетов N должно быть двоично -рациональным, т. е. N = 2n , где n = 1, 2,... , i - определяет номер точки дискретного интервала определения a = 0, 1,..., N-1.
Формулы дискретного ряда Уолша имеют вид:
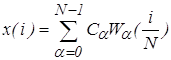 ,(9)
,(9)
где дискретный спектр Уолша
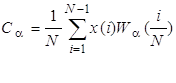 . (10)
. (10)
Для проверки правильности расчета спектральных коэффициентов может быть использовано равенство Парсеваля:
 (11)
(11)
График дискретной функции Уолша, упорядоченных по Пели приведен на рис.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() W0
W0
![]()
![]() 0 1 2 3 4 5 6 7i
0 1 2 3 4 5 6 7i
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() W1
W1
![]()
![]()
![]()
![]()
![]() W2
W2
![]()
![]()
![]()
![]()
![]()
![]() W3
W3
![]()
![]()
![]()
![]()
![]()
![]() W4
W4
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() W5
W5
![]()
![]()
![]()
![]()
![]() W6
W6

W7![]()
![]()
![]()
![]()
![]()
Рис. 4 График дискретной функции Уолша
Для ускорения дискретных преобразований Уолша используются алгоритмы быстрого преобразования Уолша (БПУ) аналогичного БПФ.
БПУ также производится прореживанием по времени и частоте.
Применение преобразований Уолша. Преобразования Уолша находят широкое применение при:
- построении цифровых фильтров;
- исследовании систем автоматического управления (моделировании, оптимизации, идентификации и т. д.);
- формировании сигналов;
- анализе и синтезе логических устройств (в теории цифровых автоматов).
Пример 2. Найти спектр Уолша - Пэли для дискретного сигнала
x(i) = i, N = 8, i = 0, 1, ...,7.
Используя формулу для Caпри N=8, в соответствии с графиком дискретной функции Уолша , приведенной на рис. 4, можно найти спектр Уолша (таб. 3).
Таблица 3
| Значения функций и спектральных коеф. при значениях индексов i и a | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| x(i)=i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
| Ca | 3,5 | -2 | -1 | 0 | -0,5 | 0 | 0 | 0 |
|
Список литературы
1. Коганов А.В. Векторные меры сложности, энтропии, информации. “Математика. Компьютер. Образование”. Вып. 7, ч. 2, “Прогресс-Традиция”, М., 2000, с. 540 — 546
2. Гольдштейн А.Л. Теория принятия решений. Задачи и методы исследования операций и принятия решений: Учеб. пособие для вузов. - Пермь: Изд-во ПГТУ, 2004.-360 с.
3. Абдулгамидов А.Р., “О системах Хаара, Радемахера и Уолша функций многих переменных”, Функциональный анализ и теория функций. 6, Учён. зап. Казан. гос. ун-та, 129, № 3, Изд-во Казанского ун-та, Казань, 1969, 53–59
4. Малозёмов В.Н., Машарский С.М. Основы дискретного гармонического анализа. Часть вторая. СПб.: НИИММ, 2003. 100 с.
5. Львович А.А., Кузьмин Б.Д. Аналитическое выражение для спектров функций Уолша // Радиотехника. 1980. Т. 35. № 1. С. 33–39.
6. Зеленков А.В. Быстрое преобразование спектра сигнала из базиса Уолша в базис дискретных экспоненциальных функций // Радиотехника и электроника. 1977. Т. 27. № 3. С. 552–565.
7. Пойда В.Н. Спектральный анализ в дискретных ортогональных базисах. Минск: Наука и техника, 1978. 136 с.
Похожие работы
... и т.д.), используемых методов (временные, частотные, операторные и т.д.) и других факторов. Наиболее часто используются следующие СБФ: – Системы единичных непрерывных и дискретных функций. – Системы тригонометрических базисных функций: . Эти функции широко используются при частотном представлении сигналов в рядах Фурье. – Системы комплексных экспоненциальных функций- . Эти функции ...
... именно соседние в сигнальном пространстве точки, которые как раз более всего подвержены возможности «перепутаться» под действием помех. 4. Характеристики приема сигналов в телекоммуникационных системах 4.1 Вероятности ошибок различения M известных сигналов Под обнаружением сигнала в радиоэлектронике понимают анализ принятого колебания y(t), завершающийся вынесением решения о наличии или ...
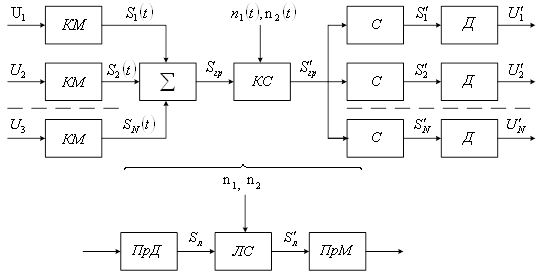
льтипликативные и аддитивные помехи. В приемнике (ПрМ) происходит обратное преобразование сигнала: . ( 5) Действие канального селектора характеризуется оператором . Процесс разделения каналов можно представить следующим образом: . ( 6) Т.е. l-ый селектор реагирует лишь на сигнал и не реагирует на сигналы других каналов. В демодуляторах (Д) ...
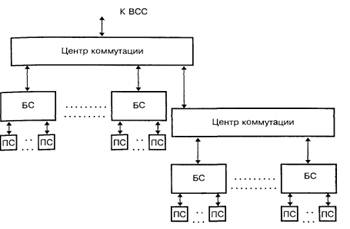
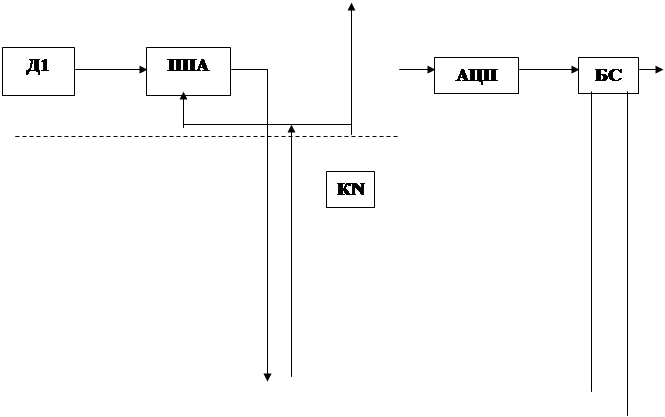
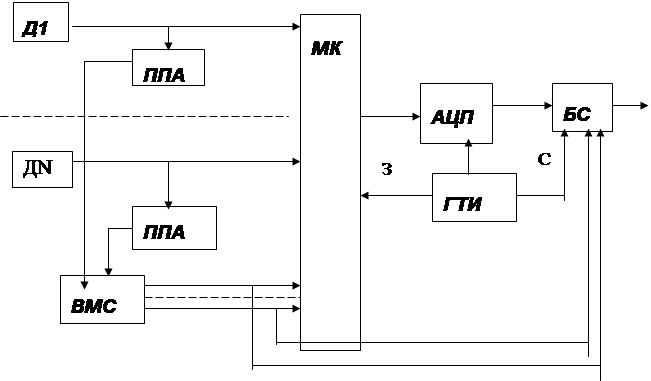
... аппаратные затраты. 1.2 Адаптивная коммутация. Адаптивная коммутация-это способ изменения частоты опроса источников информации в соответствии со скоростью изменения входного сигнала. Основная проблема такой системы сжатия: объединение потоков отсчётов, которые идут с разной частотой, в единый поток с постоянной частотой, определяемой пропускной способностью канала. Очерёдность передачи от разных ...
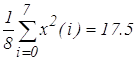
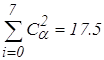
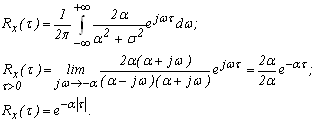
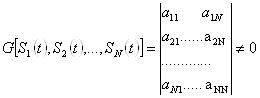

0 комментариев