Навигация
2.2 Понятие фазовой скорости
Проследим движение точки «а», соответствующей некоторому замороженному значению полной фазы (wt-bx)=j=const, вдоль линии (см. рис. 1).
Запишем выражение для полной фазы в виде ![]() , определим фазовую скорость (путь, деленный на время) следующим образом:
, определим фазовую скорость (путь, деленный на время) следующим образом:
![]() .
.
В лекционном курсе было показано, что в высокочастотной части спектра, когда можно считать wL>>R, wC>>G, можно воспользоваться приближением ![]() . В этом случае
. В этом случае ![]() , т.е. фазовая скорость не зависит (слабо зависит) от частоты;
, т.е. фазовая скорость не зависит (слабо зависит) от частоты;
Для низкочастотной части спектра, когда wL<<R, wC<<G, можно принять ![]() . В этом случае фазовая скорость нелинейно зависит от частоты
. В этом случае фазовая скорость нелинейно зависит от частоты
![]() .
.
Дальнейшее изложение проведем в два этапа. Сначала рассмотрим систему (линию) без частотной дисперсии и без потерь. Введем величину ![]() . Это время, в течение которого некоторая выбранная точка постоянной фазы перемещается от начала к концу линии. Выражение (5)
. Это время, в течение которого некоторая выбранная точка постоянной фазы перемещается от начала к концу линии. Выражение (5) ![]() перепишем с учетом
перепишем с учетом ![]() и
и ![]() . Значение
. Значение ![]() подставим в (5) и получим
подставим в (5) и получим ![]()
Вернемся к (3), запишем ![]()
В области функций времени: ![]()
![]() (6)
(6)
Это выражение представляет собой прямую иллюстрацию запаздывания на время t выходного сигнала относительно входного. Как видно, в линии без потерь выходной сигнал есть точная копия входного. Если сделанное выше допущение об отсутствии затухания в линии снять, то при a=сonst¹0, ![]() ,
, ![]() ; а выражение для выходного сигнала приобретает вид:
; а выражение для выходного сигнала приобретает вид:
![]() (7)
(7)
Это выражение отражает уменьшение уровня выходного cигнала (затухание) относительно входного. Учет частотной дисперсии показывает, что в линии могут происходить более сложные изменения сигнала.
2.3 Искажение сигнала вследствие частотной дисперсии. Групповая скорость
На рис. 2а и 2б показаны спектральная плотность ![]() для радиоимпульса и фазочастотая характеристика линии
для радиоимпульса и фазочастотая характеристика линии ![]() . Значения частот w н и w в-это тем или иным способом выбранные нижнее и верхнее граничные значения практически необходимой полосы спектра сигнала. Если в общем случае
. Значения частот w н и w в-это тем или иным способом выбранные нижнее и верхнее граничные значения практически необходимой полосы спектра сигнала. Если в общем случае ![]() ¹сonst, то ясно что «спектральные продукты» из ближайшей окрестности точек wн и wв будут распространяться с разной фазовой скоростью. Это неизбежно приведет к определенной (и довольно сложной) «деформации» выходного спектра и, следовательно, соответствующей деформации Uвых (t).
¹сonst, то ясно что «спектральные продукты» из ближайшей окрестности точек wн и wв будут распространяться с разной фазовой скоростью. Это неизбежно приведет к определенной (и довольно сложной) «деформации» выходного спектра и, следовательно, соответствующей деформации Uвых (t).
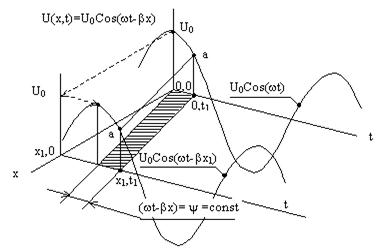
Рис. 1. К понятию фазовой скорости и запаздывания сигнала в линии без потерь
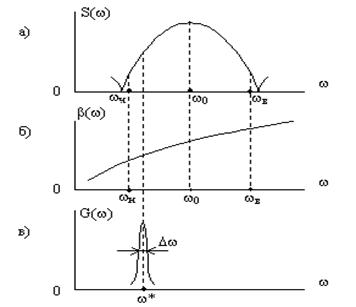
Рис. 2. К понятию групповой скорости в линии с частотной дисперсией.
Понятие «фазовая скорость» с математической точки зрения присуще волне, гармоническому колебанию на бесконечной оси времени.
Известно, что ордината функции ![]() интерпретируется как плотность бесконечно малых по уровню и сколь угодно близких по частоте гармоник. Поэтому применительно к различным участкам спектральной плотности принято оперировать понятием не фазовой, а так называемой групповой скорости.
интерпретируется как плотность бесконечно малых по уровню и сколь угодно близких по частоте гармоник. Поэтому применительно к различным участкам спектральной плотности принято оперировать понятием не фазовой, а так называемой групповой скорости.
Групповая скорость определяется следующим образом:
![]() . (8)
. (8)
Узкому участку спектральной плотности сигнала сопоставляется спектральная плотность ![]() некоторого «квазигармонического колебания», изменение мгновенных значений которого так медленно, что
некоторого «квазигармонического колебания», изменение мгновенных значений которого так медленно, что ![]() (см. рис. 2в).
(см. рис. 2в).
В теории волновых процессов такое колебание принято называть квазигармонической группой. Групповая скорость, понимаемая как выражение (8), не должна интерпретироваться как скорость перемещения в пространстве какого-либо материального объекта. Это не скорость распространения энергии или скорость распространения импульса сигнала в линии.
Любое колебание конечной длительности, например, ограниченный по времени импульс, имеет неограниченный спектр и поэтому групповая скорость не равна скорости перемещения импульса.
Фазовая и групповая скорости связаны следующим образом:
![]() . (9)
. (9)
Так как фазовая скорость с уменьшением частоты (с возрастанием длины волны) уменьшается, то производная ![]() отрицательна. Из этого следует вывод о том, что групповая скорость всегда должна быть больше или равна фазовой.
отрицательна. Из этого следует вывод о том, что групповая скорость всегда должна быть больше или равна фазовой.
Вернемся к рис. 2. и подчеркнем следующее:
Пусть вычислены Vгр, н для окрестности точки wн и для окрестности точки wв. Тогда абсолютная величина разности времен прихода двух крайних групп к концу линии длиной ℓ составит:
![]() (10)
(10)
Ясно, что искажения импульсного сигнала будут очень велики, если интервал Dt сопоставим по величине с длительностью импульса tи. Если Dt<<tи, то дисперсионные искажения малы и, скорее всего, ими можно пренебречь. Видно, что если линия достаточно длинная, то существенные дисперсионные искажения можно получить даже при малой разности групповых скоростей (малой скорости передачи, большой длительности tи).
Результатом проявления дисперсии является «расплывание» импульса во времени. Если в линию отправлены два близко расположенных импульса (на соседних тактовых интервалах), то «отклики» от них на выходе линии могут «накладываться» друг на друга, («интерферировать» в силу принципа суперпозиции) и тем самым дополнительно затруднять процедуру опознавания сигналов на приемной стороне.
3. Моделирующая программа LINE2
Моделирующая программа LINE2 предназначена для наблюдения на экране монитора «отклика» (выходного сигнала UN(t)) проводной линии связи в ответ на входное воздействие в форме одиночных импульсных сигналов, а также их последовательностей с целью изучения влияния на выходные сигналы параметров линии. Предусматривается возможность исследования воздушных и кабельных линий.
Похожие работы
... до тех пор, пока во время счета не выполнится вход в блок, и котором описан массив. При входе в блок вычисляются границы массива и производится обращение к программе распределения памяти для массивов. Здесь же вносится в информационный вектор необходимая информация. Какая информация заносится в информационный вектор? Для предложенной выше n-мерной схемы нам как минимум нужны ...
... .) В системах, в которых страницы инструкций (в противоположность страницам данных) являются реентерабельными, бит изменения никогда не устанавливается. 2. Разработка алгоритма управления оперативной памятью Ниже приведён алгоритм управления оперативной памятью в системе Linux. В основе всего лежат страницы памяти. В ядре они описываются структурой mem_map_t. typedef struct page { /* ...
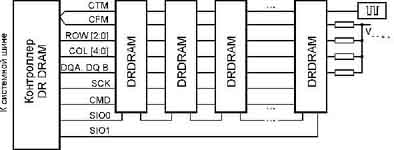
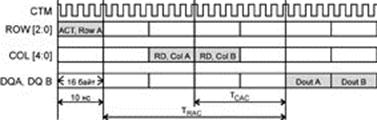
... производительность 1600 Мбайт/с на двухбайтной шине данных при частоте 400 МГц. Стандарт DRDRAM поддержан множеством производителей микросхем и модулей памяти, он претендует на роль основного высокопроизводительного стандарта для памяти компьютеров любого размера. Подсистема памяти (ОЗУ) DRDRAM состоит из контроллера памяти, канала и собственно микросхем памяти. По сравнению с DDR SDRAM при той ...
... . Несет информацию об адресе текущего элемента однонаправленного динамического списка. q – указатель на структуру news. Несет информацию об адресе последнего созданного элемента однонаправленного динамического списка. news *un,*p,*q; i – переменная типа int. Несет информацию о количестве элементов однонаправленного динамического списка. int i; 4 2) Локальные переменные процедуры ...
0 комментариев