Навигация
Влияние фазовых отклонений
2. Влияние фазовых отклонений
Подобно тому как это было сделано при рассмотрении линз, выясним ряд вопросов, связанных с влиянием фазовых искажений в раскрыве антенны. Обычно в раскрыве зеркала допускается фазовое отклонение Δφ= π/2.
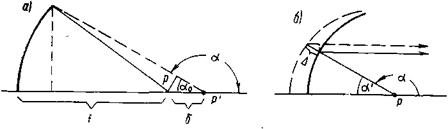
Рис.6
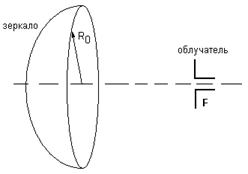
![]() На рис.6а показано изменение хода центрального и крайнего лучей при смещении облучателя зеркала вдоль фокальной оси. Разность их фаз в раскрыве есть
На рис.6а показано изменение хода центрального и крайнего лучей при смещении облучателя зеркала вдоль фокальной оси. Разность их фаз в раскрыве есть ![]()
откуда допустимое смещение равно
Смещение облучателя – не единственная причина фазового отклонения в раскрыве, поэтому принято брать Δφ = π/8
![]() Тогда
Тогда
![]() Выбор необходимой точности изготовления зеркала поясняется рис.6б, где пунктиром показан требуемый профиль зеркала, а сплошной линией -фактически выполненный. Составляя разность хода лучей и соответствующую разность фаз
Выбор необходимой точности изготовления зеркала поясняется рис.6б, где пунктиром показан требуемый профиль зеркала, а сплошной линией -фактически выполненный. Составляя разность хода лучей и соответствующую разность фаз
|
|
(Δ-отклонение некоторой точки поверхности зеркала вдоль луча точечного источника), получаем следующее выражение для линейного допуска:
![]()
и если разрешается Δφ = π/8, то
Наименьшее отклонение допускается в центре зеркала зеркала (а' = 0):
![]()
Итак, по краям зеркало может быть сильнее деформировано без существенного ухудшения его свойств.
3. Направленность действия параболического зеркала
Поле излучения, создаваемое зеркалом, в принципе можно найти, зная наведенный облучателем на его поверхности электрический ток. Вместо тока на «освещенной» стороне можно рассматривать поле в плоскости раскрыва, которое заменяется электрическим и магнитным эквивалентными поверхностными токами либо распределением источников типа элемента Гюйгенса. Однако и для определения тока на поверхности зеркала, и для нахождения поля в его раскрыве нет иного практического приема, кроме предположения, что каждый элемент зеркала действует как элемент плоскости, что, естественно, дает лишь приближенный результат. При этом, в частности, не учитываются краевая дифракция и токи на «неосвещенной» стороне зеркала.
![]() Согласно известному правилу плотность поверхностного тока зеркала есть
Согласно известному правилу плотность поверхностного тока зеркала есть
где Нs — магнитное поле на металлической поверхности.
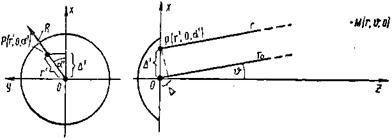
Рис. 7
Каждый ее элемент, как уже отмечалось, принимается за участок бесконечной плоскости, и соответственно этому Нs находится как удвоенная (при отражении) касательная к зеркалу компонента магнитного поля облучателя Н:
![]()
По известной характеристике направленности облучателя (обычно считают, что зеркало находится в его дальней зоне) вычисляют распределение тока на всем зеркале. Затем поле излучения зеркала находится как суперпозиция полей всех излучающих элементов. Это можно сделать как путем непосредственного интегрирования полей, создаваемых токами зеркала в дальней зоне, так и при помощи векторного потенциала.
Второй способ определения направленности действия зеркальной антенны, при котором исходят из поля в его раскрыве, называется «апертурным». Пусть рассматривается зеркало в виде параболоида вращения, и поле в раскрыве по известной характеристике облучателя уже найдено. Объяснению дальнейших действий служит рис.7, на котором дальнее поле описывается в сферических координатах (r, υ, α), а поле в раскрыве — в штрихованных сферических координатах (r, 90°-ύ, α'). Дальняя точка наблюдения М (r, υ, α) лежит в плоскости α = 0, являющейся также плоскостью чертежа. Начало координат находится в центре раскрыва, и соответственно этому в раскрыве υ' = 90°,
Пусть комплексная амплитуда электрического поля излучения в точке М (r, υ , 0), создаваемого элементом раскрыва в окрестности точки Р (r', 0, α'), есть
![]()
где q(r', α') - взятая с требуемой амплитудой функция плотности источников в раскрыве . Как видно из рис. 7, ![]()
причем ![]()
Учитывая это и интегрируя dЕm по раскрыву, имеем следующее выражение для электрического поля дальней зоны антенны в плоскости α = 0:
|
|
Для получения простого результата идеализируем задачу, взяв qm(r', α') = e0 const, т. е., в сущности, приняв раскрыв зеркала за идеальную поверхностную антенну в форме круга. Тогда
|
|
Принимая во внимание, что интегрирование по α' приводит к функции Бесселя нулевого порядка, которая имеет интегральное представление
![]()
пишем
![]()
а интегрирование по r' дает
|
|
Из этого выражения нетрудно получить нормированную характеристику направленности зеркала в меридиональной плоскости учитывая, что
![]()
В результате
|
|
Далее, нетрудно найти угловую ширину главного максимума излучения по нулям. Первый корень уравнения J1 (x) = 0 равен В11 = 3,832.
Полагая sin υ0 ≈ υ0, имеем
|
|
Полученные формулы оказываются более достоверными для длиннофокусных зеркал, облучаемых обычно равномернее, чем короткофокусные.
Учет действительных характеристик направленности реальных облучателей требует уже весьма громоздких математических действий, которые не приводятся. Остановимся лишь на некоторых результатах, обычно используемых при расчете зеркальных антенн.
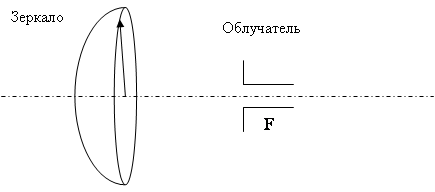
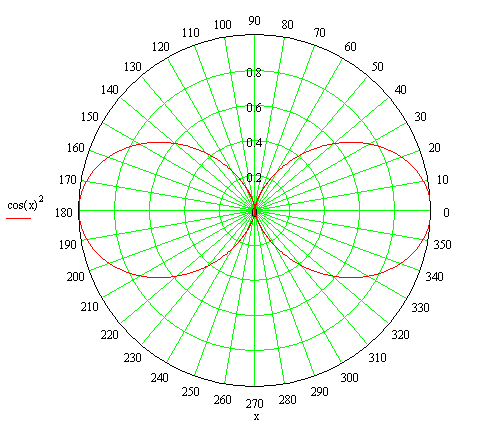
Подробнее других изучено параболическое зеркало, облучаемое элементарным электрическим вибратором, снабженным плоским контррефлектором (рис.8). Характеристика направленности в меридиональной плоскости при этом выражается формулой
|
|
![]() Где
Где
|
|
Знак плюс берется в том случае, когда меридиональная плоскость проходит через облучающий вибратор (плоскость Е), а минус — в случае перпендикулярной вибратору меридиональной плоскости (плоскость Н).
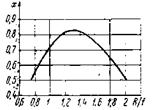
Кнд антенны в которой коэффициент использования раскрыва x равен:
![]()
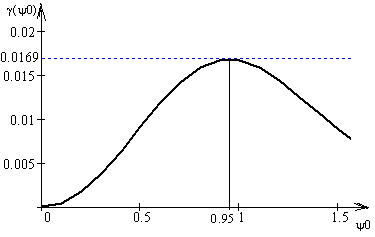
График функции х(R/f) показывает, что найвыгоднейшим при данном типе облучателя является отношение радиуса зеркала к фокусному расстоянию:
![]()
при котором
![]()
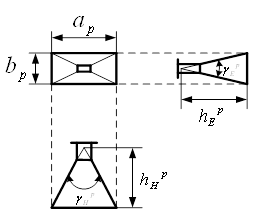
Существование оптимума объясняется следующим образом: при удалении облучателя кнд антенны должен был бы возрастать в результате повышения равномерности облучения, однако при этом уменьшается угол, под которым видно зеркало (рис.8а), так что увеличивается доля энергии, уходящей за его край, что снижает кнд.
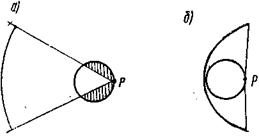
Рис.8
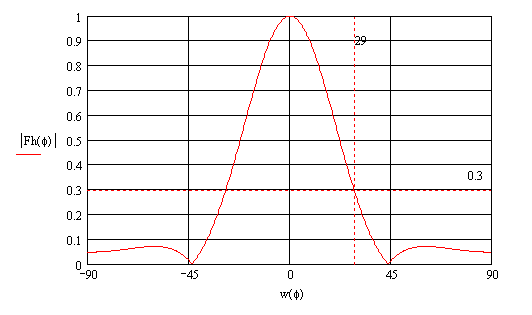
Короткофокусное зеркало (рис.8б) облучается почти без потерь, но неравномерно. Можно убедиться, что максимальный коэффициент использования соответствует состоянию, при котором амплитуда поля дипольного облучателя на краю зеркала составляет около 1/3 максимальной.
На рис.9а, б показано распределение тока в зеркале при дипольном облучателе. Ток, наводимый на короткофокусном зеркале (рис.9б), собирается у двух полюсов, расположение которых нетрудно определить из рис.9в: они лежат на пересечениях оси облучателя с поверхностью параболоида.
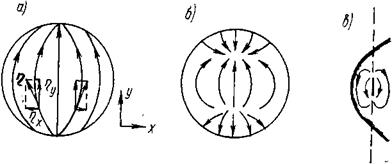
Рис. 9
В результате существования полюсов часть зеркала несет противофазный ток, уменьшающий излучение в осевом направлении. Как говорят, зеркало имеет при этом «вредные зоны». Однако и в тех случаях, когда вредных зон нет, нельзя игнорировать специфического искривления линий тока в результате неоднородности поля облучателя.
Похожие работы
... зеркала равен, таким образом, , а на периферии зеркала может быть менее жёстким. [2] Допуск в центральной части зеркала ; допуск для большего угла раскрыва ; допуск для меньшего угла раскрыва . 4.5 Описание конструкции Полученная зеркальная антенна состоит из следующих частей (см. приложение): 1) рефлектор (зеркало), представляющий собой усечённый параболоид вращения, и выполненный из т
... её параметры: размеры, глубина фокус, коэффициент усиления зависят от длины волны, поэтому близкие к полученным характеристикам она будет иметь в окрестности данной длины волны. 4. принцип действия зеркальной антенны Электромагнитная волна, излученная облучателем, достигнув проводящей поверхности зеркала, возбуждает на ней токи, которые создают вторичное поле, обычно называемое полем ...
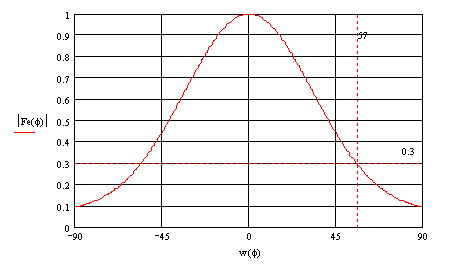
... поля. В данном случае распределение напряженности возбуждающего поля в основном определяется диаграммой направленности облучателя в соответствующей плоскости. Выражение для нормированной диаграммы направленности зеркальной параболической антенны при этом имеет вид: , где -цилиндрические функции Бесселя первого и второго порядка; - коэффициент, показывающий во сколько раз амплитуда возбуждающего ...
... с неравномерным распределением напряжённости возбуждающего поля. В данном случае распределение напряжённости возбуждающего поля в основном определяется ДН облучателя в соответствующей плоскости. Выражение для нормированной ДН зеркальной параболической антенны при этом имеет вид: , где J1, J2 – цилиндрические функции Бесселя первого и второго порядка. - Коэффициент, показывающий во ...
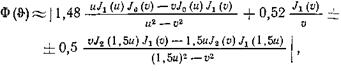

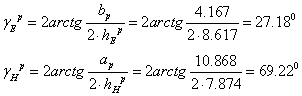

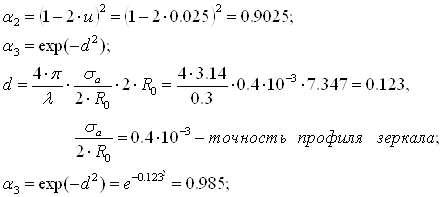
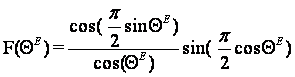
0 комментариев