Дифракційна решітка. Кутова дисперсія і роздільна здатність дифракційної решітки

3. Дифракційна решітка. Кутова дисперсія і роздільна здатність дифракційної решітки

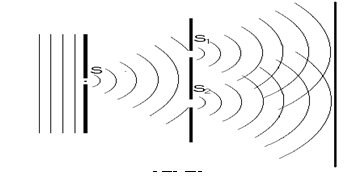
Дифракційною решіткою називається оптичний прилад, який складається з великої кількості однакових щілин, розділених між собою однакової ширини непрозорими проміжками. Відстань d між серединами двох сусідніх щілин, називається сталою дифракційної решітки.

Якщо розмістити паралельно решітці збірну лінзу, то в її фокальній площині на екрані можна буде спостерігати результати дифракції світла від решітки (рис.4).

Оптична різниця ходу променів від двох сусідніх щілин дорівнює

(21)

Оптична різниця фаз в цьому випадку буде дорівнювати

(22)

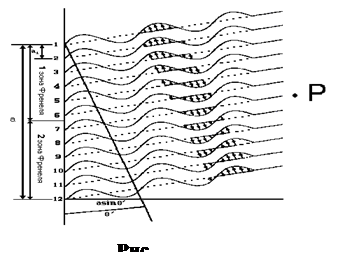
В точку P на екрані приходять промені від усіх щілин. Всі ці промені зсунуті по фазі на однакову величину .

Для знаходження результуючої амплітуди всіх хвиль, які прийшли в точку Р слід скористатися формулою результуючої амплітуди при інтерференції багатьох хвиль

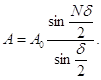(23)

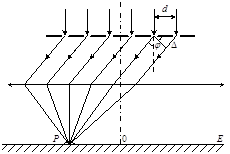
Рис. 4

З урахуванням (22) результуюча амплітуда  буде дорівнювати

(24)

де  – амплітуда хвиль від однієї щілини;  – число щілин у решітці;  – стала дифракційної решітки;  – довжина хвилі монохроматичного світла.

Проведемо аналіз формули (24).

а) Якщо вираз у знаменнику (24) досягає мінімуму, тобто буде дорівнювати нулю, то амплітуда  буде найбільшою. Ця умова є умовою максимуму дифракції на дифракційній решітці, тобто

,

звідки

. (25)

Формула (25) є умовою головних максимумів дифракції на дифракційній решітці.

б) Побічні максимуми дифракції можна одержати, якщо чисельник у формулі (24) досягає максимуму. Це можливо за умови, коли

(26)

Після скорочення одержимо

(27)

Вираз (27) є умовою побічних максимумів дифракції на дифракційній решітці.

в) Побічні мінімуми дифракції на дифракційній решітці одержуємо із умови коли чисельник формули (25) буде найменшим, тобто коли

(28)

звідки

(29)

Формула (29) є умовою побічних мінімумів на дифракційній решітці.

Дифракція світла на дифракційній решітці, яка має N щілин показана на рис.5.

Рис.5

Розрахунки показують, що  Для достатньо великих значень N побічні мінімуми і побічні максимуми не проявляються. Число головних максимумів дифракції визначається відношенням d до λ (), при цьому .

Важливо знати:

а) Внаслідок немонохроматичності біле сонячне світло після проходження дифракційної решітки дає максимуми ІІ, ІІІ і більш високих порядків у вигляді спектрів.

б) Хороша решітка з малим d і великим N дає дифракційні спектри з великою роздільною здатністю. Характерною ознакою дифракційних спектрів є рівномірний розподіл кольорів у спектрі. На відміну від дифракційного спектра, призматичний спектр стиснутий в області червоних кольорів і розширений в області фіолетових кольорів.

Кожна дифракційна решітка характеризується кутовою дисперсією, яка позначається буквою Д

(30)

де  – кутова відстань між спектральними лініями, які відрізняються за довжиною хвилі на величину .

Для знаходження кутової дисперсії дифракційної решітки слід продиференціювати формулу головних максимумів дифракції , тобто

звідки

В межах невеликих кутів , тому можна вважати, що

(31)

Таким чином кутова дисперсія обернено пропорційна періоду решітки d. Чим вищий порядок спектра k, тим більша дисперсія.

Роздільною здатністю спектрального приладу, а таким є дифракційна решітка, називають безрозмірну величину

(32)

де R – роздільна здатність; λ – довжина хвилі;  – мінімальна різниця довжин хвиль двох сусідніх спектральних ліній, при якій ці лінії спостерігаються роздільно, якщо виконується умова Релея. Згідно з умовою Релея дві спектральні лінії будуть видимі роздільно у випадку, коли мінімум другої спектральної лінії знаходиться не ближче максимуму першої лінії (рис.6).

Рис.6

Знайдемо роздільну здатність дифракційної решітки. За умовою Релея максимум першої лінії в крайньому випадку співпадає з мінімумом другої спектральної лінії. Якщо спектральні лінії будуть розміщені ближче ніж , то жоден спектральний прилад розділити їх не зможе.

Запишемо умову головного максимуму для другої спектральної лінії

(33)

Умова першого побічного мінімуму для другої лінії

(34)

Оскільки ліві частини однакові, то прирівняємо праві частини цих рівнянь

або

звідки

де  – порядок спектру;  – число всіх щілин у решітці.

4. Дифракція рентгенівських променів на просторовій решітці. Формула Вульфа-Брегга

Рентгенівське випромінювання має значно менші довжини хвиль ніж видиме світло. Звичайні дифракційні решітки для рентгенівського випромінювання використати не можливо, так як . У цьому випадку використовують кристалічні структури, стала решітки яких збігається за розмірами з .

Плоскі вторинні хвилі, які відбиваються від різних атомних шарів є когерентними, а тому будуть давати інтерференцію один з одним (рис.7).

З рис.7 видно, що різниця ходу двох хвиль, відбитих від сусідніх атомних шарів дорівнює АВ + ВС = , де d – стала кристалічної структури;  – кут ковзання. Для максимумів дифракції на просторовій решітці

. (36)

Рис.7

Формула (36), яка має назву формули Вульфа - Брегга, має досить велике практичне використання в спектральному та структурному аналізах при вивченні властивостей твердих тіл.