Навигация
Понятие о жизненном цикле систем
5 Понятие о жизненном цикле систем.
Под жизненным циклом любой системы понимается промежуток времени, который проходит между осознанием необходимости в этом изделии и осознании его ненужности. Между этими моментами существует ряд этапов.
К примеру, в экономике это следующая последовательность:
Маркетинг.
Проектирование и разработка.
Материально-техническое снабжение производственных процессов.
Подготовка и разработка технологических процессов.
Производство.
Контроль, проведение испытаний и наблюдений.
Упаковка и хранение.
Реализация изделия.
Монтаж, эксплуатация.
Техническая помощь.
Утилизация.
Модель объекта должна строиться так, чтобы любой фрагмент был доступен на каждом этапе жизненного цикла.
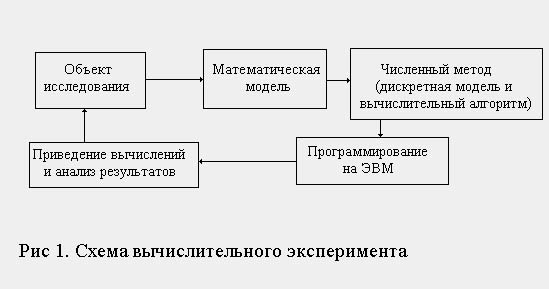
Взаимодействие модели и объекта исследования происходит на нескольких этапах:
Моделирование в виртуальном мире объектов реального мира.
Создание и развитие виртуального мира.
Воплощение объектов виртуального мира в реальном мире.
 Любой объект можно представить как «черный ящик», на который воздействуют различные факторы.
Любой объект можно представить как «черный ящик», на который воздействуют различные факторы.
Z – вектор контролируемых возмущений.
Y – неконтролируемый вектор выходных параметров.
U – контролируемый вектор управляющих воздействий на технологический процесс.
W – вектор неконтролируемых возмущений.
Затем выполняется формализация, и объект представляется в следующем виде:

Y – вектор выходных параметров.
X – вектор контролируемых входных переменных. (Объединяет действия переменных U, Z).
E – случайная аддитивная помеха (суммарная), которая характеризует влияние случайных возмущений.
F (B,x) – параметрическая функция, которая осуществляет преобразование значений Х в Y, или это модель изучаемого объекта.
Предметом исследования модели является определение вида модели и параметров модели. Истинного значения параметров системы узнать невозможно, можно получить только оценку параметров любой модели (вектора В). Изменяя значения параметров Х можно наблюдать изменение поведения выходных значений Y, или поддерживать Y на постоянном уровне.
Изменение Х определяется либо объективными возможностями существования данного фактора, либо нормативами. Чем меньше количество управляемых факторов, тем лучше управлять системой в целом.
Входные параметры считаются независимыми, или экзогенными.
Выходные параметры считаются зависимыми, или эндогенными.
Модели прогнозирования.
Существует множество математических моделей, посредством которых решаются те, или иные задачи. Во всех сферах деятельности человека важным моментом является прогнозирование последующих событий. Сейчас существует более 100 методов и методик прогнозирования, Условно их можно разделить на фактографические и экспертные. Фактографические методы основаны на анализе информации об объекте, а экспертные – на суждениях экспертов, которые получены при проведении коллективных или индивидуальных опросов. Среди фактографических методов можно выделить следующие:
Статистические методы.
Методы аналогии.
К статистическим методам относятся аппроксимация, интерполяция, , методы исследования временных рядов.
К методам аналогии относятся модели планирования эксперимента, а также математические, исторические и другие аналогии.
Среди моделей прогнозирования можно выделить следующие:
Модели аппроксимации.
Методы аппроксимации применимы к детерминированным и статистическим системам.
Аппроксимация – приближение (с лат.).
Выбор аппроксимирующей функции F(B,x) связан с решением оптимизационной задачи. Для этого применяется критерий минимизации квадратичной ошибки.
Постановка задачи.
Пусть проведено N(xI,yI) опытов, где
xI - входной параметр;
yI - выходной параметр.
Необходимо подобрать модель связывающую x и y.

Через точки (xI,yI) можно провести кривую, которая, в свою очередь, может проходить через эти точки или находиться вблизи данных точек.
В аппроксимации для получения параметров модели используется МНК-критерий (метод наименьших квадратов). Лучшей считается та модель, для которой сумма квадратов отклонений опытных значений, от теоретических будет минимальной.
Для этого формируется целевая функция или критерий оптимизации.
S = ∑ (yI – F(B, xI))2 – min.
Далее надо исследовать функцию на экстремум. Неизвестными будут коэффициенты модели B. Наиболее просто находятся параметры, если F(B, xI) представляет собой полином n-ной степени. При этом формируется система линейных уравнений, порядок которой на единицу больше степени полинома.
К примеру, для полинома 3-ей степени система будет выглядеть так:
![]()
![]()
![]()
![]()
![]()
![]() N ∑ xI ∑ xI2 ∑ yI b0
N ∑ xI ∑ xI2 ∑ yI b0
С = ∑ xI ∑ xI2 ∑ xI3 D = ∑ xI yI B = b1
∑ xI2 ∑ xI3 ∑ xI4 ∑ xI2 yI b2
C – матрица коэффициентов системы.
D – вектор-столбец свободных членов.
B – вектор неизвестных.
В общем случае для нахождения параметров формируется система дифференциальных уравнений. В конце формируется система линейных уравнений, которую можно решать точными методами (метод Крамера, Гауса, обратной матрицы). Когда система решена, то есть, найдены параметры модели, можно выполнить прогнозирование значений y.
Если выбираемое x находится внутри элементарного интервала ∆x, то говорят о прогнозировании в настоящем. Если x меньше x0, или x больше xN, то речь идет об экстраполяции.
Модели интерполяции.
В интерполяции, в отличие от аппроксимации, производится минимизация линейной ошибки. Также, в отличие от аппроксимации, где кривая по отношению к точкам опытов может располагаться любым образом, а именно находиться вблизи этих точек, или проходить через некоторые из них, кривая интерполяции, или интерполяционный полином обязательно проходит через все точки кривой, которые называются узлами.
Наиболее простой подход к получению интерполяционной модели был предложен Лагранжем. Так как полином проходит через каждую опытную точку, то нужно составить столько уравнений, сколько проведено опытов. В левой части уравнения формируется полином, проходящий через i-тую точку. В правой части формируется вектор значений y. В результате получается система линейных уравнений n-ого порядка, где n – число опытов, а степень интерполяционного полинома на единицу меньше числа опытов.
Количество опытов должно обязательно быть больше пяти, иначе результаты интерполирования будут не пригодны для прогнозирования. Так как метод интерполяции требует прохождения модели через все точки, то накладываются определенные условия на опытные значения. Разности i-ого порядка должны быть примерно одинаковы малы. Хорошо интерполируются монотонные функции.
Оба рассмотренных метода относятся к методам исследования детерминированных моделей.
Анализ временных рядов.
Временные ряды отражают тенденцию изменения параметров системы во времени, поэтому входным параметром х является момент времени.
Выходной параметр y называется уровнем ряда. В случае отсутствия ярко выраженных изменений в течение времени, общая тенденция сохраняется. Ряд можно описать уравнением вида
YT = F (t) + ET , где
F (t) – детерминированная функция времени.
ET – случайная величина
Во временных рядах проводится операция анализа и сглаживания тренда, который отражает влияние некоторых факторов. Для построения тренда применяется МНК-критерий.
Существуют моментальные и интервальные ряды. В моментальных рядах отражаются абсолютные величины, по состоянию на определенный момент времени, а в интервальных – относительные величины (показатель за год, месяц, и т.д.). Исследование данных при помощи рядов позволяет во многих случаях более четко представить детерминированную функцию. При этом рассчитываются базисные и цепные показатели (прирост, коэффициент роста, коэффициент роста, темп роста, темп прироста, и др.). Под базисными показателями понимают, показатели, которые соотносятся к начальному уровню ряда. Цепные показатели относятся к предыдущему уровню.
Прогноз явлений по временным рядам состоит из двух этапов:
Прогноз детерминированной компоненты.
Прогноз случайной компоненты.
Обе проблемы связаны с анализом результатов парных экспериментов. В отличие от аппроксимации и интерполяции анализ временных рядов включает в себя методы оценки случайных компонент. Поэтому прогнозирование при помощи временных рядов является более точным.
Исследование рядов имеет большое значение и для технических, и для экономических систем.
Выводы
Любая информация может быть получена на основании прошлого опыта, а именно теории проверенной практикой (научные факты, методики и расчеты, опыт каждого человека).
Новая информация может быть получена путем наблюдения, то есть, изучением системы без вмешательства в её функционирование. Также она может быть получена путем эксперимента, то есть, изучая систему при целенаправленном воздействии на её параметры.
Модель исследуется для того, чтобы можно было управлять исследуемым объектом или системой, на основании полученной по модели информации. Управление системы связано с улучшением его характеристик или её стабилизацией, то есть с возможностью прогнозирования поведения систем.
Список литературы
Губарев В.В. Концептуальные основы информатики: Учеб. Пособие: Новосибирск: Изд-во НГТУ, 2001г.
Ивченко Б. П., Мартыщенко Л.А. Информационная микроэкономика Часть 1: Методы анализа и прогнозирования. СПб. Нордмед-Издат. 1997г.
Турчак К. Численные методы. М.- 1985г.
Шелобаев С.И. Математические методы и модели в экономике, финансах и бизнесе: Учеб. Пособие для вузов. М.- 2000г.
Черчмен У., Акоф Р., Арноф Я. Введение в исследование операции М. – Наука 1968г.
Похожие работы
... гидродинамического режима системы могут изменяться виды моделей [1]. Цель данной курсовой работы – создать математическую модель процесса получения эмульгатора (применяемого для стабилизации эмульсий «масло в воде») из масла и триэтаноламина и дать характеристику этой модели. Математическое моделирование данного процесса заключается в расчёте значений концентраций реагентов и величин потоков на ...
... целом как сложной системы в различных условиях. Вычислительные эксперименты с математическими моделями дают исходные данные для оценки показателей эффективности объекта. Поэтому математическое моделирование как методология организации научной экспертизы крупных проблем незаменимо при проработке народнохозяйственных решений. (В первую очередь это относится к моделированию экономических систем[6]). ...
... моделирование широко используется там, где экспериментальные исследования трудоемки и дорогостоящи, или вообще невозможны (например, в изучении социальных явлений). Кроме задачи о прогнозе, математическое моделирование помогает классифицировать и систематизировать фактический материал, увидеть существующие связи в мозаике фактов. Это вытекает из того, что модель является специфическим -ярким и ...
... своевременное распределение средств на развитие. Данными вопросами я и занимаюсь в настоящей дипломной работе. 4. Математическое моделирование Интернет - услуг 4.1 Математическое моделирование dial-up подключений Сначала рассмотрим моделирование услуги предоставления доступа в Интернет по dial-up, так как данная услуга является показателем потенциальных абонентов для монопольной услуги ...

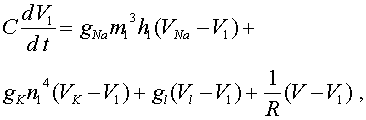
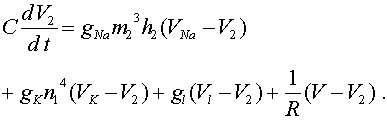
0 комментариев