Навигация
Найти оптимальный план транспортной задачи
3.4. Найти оптимальный план транспортной задачи.
![]()
![]()
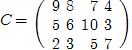
Решение
Запишем условие задачи в экономическом виде на основании таблицы, где заданы пункты отправления и назначения, запасы и потребности [1, c. 135].
| Пункты отправления | Пункты назначения | Запасы | |||
| B1 | B2 | B3 | B4 | ||
| A1 | 9 | 8 | 7 | 4 | 220 |
| A2 | 5 | 6 | 10 | 3 | 120 |
| A3 | 2 | 3 | 5 | 7 | 150 |
| Потребности | 200 | 200 | 140 | 180 | 720\490 |
Поскольку запасы и потребности не совпадают, имеем задачу с неправильным балансом или открытую, следовательно введем фиктивный пункт отправления с количеством 230 единиц груза.
1) Диагональный метод
Найдем опорный план диагональным методом [1, c. 140].
| B A | 1 | 2 | 3 | 4 | a | |||||
| 200 | 200 | 140 | 180 | |||||||
| 1 | 220 | 9 | 8 | 7 | 4 | 0 | ||||
| 200 | 20 | – | 0 | + | ||||||
| 2 | 120 | 5 | 6 | 10 | 3 | –2 | ||||
| 120 | ||||||||||
| 3 | 150 | 2 | 3 | 5 | 7 | –5 | ||||
| 60 | + | 90 | – | |||||||
| 4 | 230 | 0 | 0 | 0 | 0 | –10 | ||||
| 50 | + | 180 | – | |||||||
| b | 9 | 8 | 10 | 10 | ||||||
Стоимость начального плана перевозки:
z0 = 200 · 9+20 · 8+120 · 6+60 · 3+90 · 5+50 · 0+180 · 0 = 3310.
Для базисных клеток система потенциалов такая:
a1+b1=9; a1+b2=8;
a2+b2=6;
a3+b2=3; a3+b3=5;
a4+b3=0; a4+b4=0.
Поскольку количество переменных меньше, чем уравнений, то положим: a1=0. Проверяем условие оптимальности для свободных клеток: a + b ≤ c
a1+b3=0+10=10 > 7 [3]; a1+b4=0+10=10 > 4 [6];
a2+b1=–2+9=7 > 5 [2]; a2+b3=–2+10=8 ≤ 10; a2+b4=–2+10=8 > 3 [5];
a3+b1=–5+9=4 > 2 [2]; a3+b4=–5+10=5 ≤ 7;
a4+b1=–10+9=–1 ≤ 0; a4+b2=–10+8=–2 ≤ 0;
Для клетки A1B4 (из тех, что не выполняется условие оптимальности) разница потенциалов наибольшая, потому для нее делаем цикл пересчета на минимальную величину отрицательных вершин: min(20, 90, 180)=20.
Переходим к следующей итерации.
| B A | 1 | 2 | 3 | 4 | a | |||||
| 200 | 200 | 140 | 180 | |||||||
| 1 | 220 | 9 | 8 | 7 | 4 | 0 | ||||
| 200 | – | 20 | + | |||||||
| 2 | 120 | 5 | 6 | 10 | 3 | 4 | ||||
| 0 | + | 120 | – | |||||||
| 3 | 150 | 2 | 3 | 5 | 7 | 1 | ||||
| 80 | + | 70 | – | |||||||
| 4 | 230 | 0 | 0 | 0 | 0 | –4 | ||||
| 70 | + | 160 | – | |||||||
| b | 9 | 2 | 4 | 4 | ||||||
Стоимость 1 плана перевозки:
z1 = 200 · 9+20 · 4+120 · 6+80 · 3+70 · 5+70 · 0+160 · 0 = 3190.
Для базисных клеток система потенциалов такая:
a1+b1=9; a1+b4=4;
a2+b2=6;
a3+b2=3; a3+b3=5;
a4+b3=0; a4+b4=0.
Поскольку количество переменных меньше, чем уравнений, то положим: a1=0. Проверяем условие оптимальности для свободных клеток: a + b ≤ c
a1+b2=0+2=2 ≤ 8; a1+b3=0+4=4 ≤ 7;
a2+b1=4+9=13 > 5 [8]; a2+b3=4+4=8 ≤ 10; a2+b4=4+4=8 > 3 [5];
a3+b1=1+9=10 > 2 [8]; a3+b4=1+4=5 ≤ 7;
a4+b1=–4+9=5 > 0 [5]; a4+b2=–4+2=–2 ≤ 0;
Для клетки A2B1 (из тех, что не выполняется условие оптимальности) разница потенциалов наибольшая, потому для нее делаем цикл пересчета на минимальную величину отрицательных вершин: min(200, 160, 70, 120)=70.
Переходим к следующей итерации.
| B A | 1 | 2 | 3 | 4 | a | |||||
| 200 | 200 | 140 | 180 | |||||||
| 1 | 220 | 9 | 8 | 7 | 4 | 0 | ||||
| 130 | – | 90 | + | |||||||
| 2 | 120 | 5 | 6 | 10 | 3 | –4 | ||||
| 70 | + | 50 | – | |||||||
| 3 | 150 | 2 | 3 | 5 | 7 | –7 | ||||
| 150 | ||||||||||
| 4 | 230 | 0 | 0 | 0 | 0 | –4 | ||||
| 0 | + | 140 | 90 | – | ||||||
| b | 9 | 10 | 4 | 4 | ||||||
Стоимость 2 плана перевозки:
z2 = 130 · 9+90 · 4+70 · 5+50 · 6+150 · 3+140 · 0+90 · 0 = 2630.
Для базисных клеток система потенциалов такая:
a1+b1=9; a1+b4=4;
a2+b1=5; a2+b2=6;
a3+b2=3;
a4+b3=0; a4+b4=0.
Поскольку количество переменных меньше, чем уравнений, то положим: a1=0. Проверяем условие оптимальности для свободных клеток: a + b ≤ c
a1+b2=0+10=10 > 8 [2]; a1+b3=0+4=4 ≤ 7;
a2+b3=–4+4=0 ≤ 10; a2+b4=–4+4=0 ≤ 3;
a3+b1=–7+9=2 ≤ 2; a3+b3=–7+4=–3 ≤ 5; a3+b4=–7+4=–3 ≤ 7;
a4+b1=–4+9=5 > 0 [5]; a4+b2=–4+10=6 > 0 [6];
Для клетки A4B2 (из тех, что не выполняется условие оптимальности) разница потенциалов наибольшая, потому для нее делаем цикл пересчета на минимальную величину отрицательных вершин: min(50, 130, 90)=50.
Переходим к следующей итерации.
| B A | 1 | 2 | 3 | 4 | a | |||||
| 200 | 200 | 140 | 180 | |||||||
| 1 | 220 | 9 | 8 | 7 | 4 | 0 | ||||
| 80 | – | 140 | + | |||||||
| 2 | 120 | 5 | 6 | 10 | 3 | –4 | ||||
| 120 | ||||||||||
| 3 | 150 | 2 | 3 | 5 | 7 | –1 | ||||
| 0 | + | 150 | – | |||||||
| 4 | 230 | 0 | 0 | 0 | 0 | –4 | ||||
| 50 | + | 140 | 40 | – | ||||||
| b | 9 | 4 | 4 | 4 | ||||||
Стоимость 3 плана перевозки:
z3 = 80 · 9+140 · 4+120 · 5+150 · 3+50 · 0+140 · 0+40 · 0 = 2330.
Для базисных клеток система потенциалов такая:
a1+b1=9; a1+b4=4;
a2+b1=5;
a3+b2=3;
a4+b2=0; a4+b3=0; a4+b4=0.
Поскольку количество переменных меньше, чем уравнений, то положим: a1=0. Проверяем условие оптимальности для свободных клеток: a + b ≤ c
a1+b2=0+4=4 ≤ 8; a1+b3=0+4=4 ≤ 7;
a2+b2=–4+4=0 ≤ 6; a2+b3=–4+4=0 ≤ 10; a2+b4=–4+4=0 ≤ 3;
a3+b1=–1+9=8 > 2 [6]; a3+b3=–1+4=3 ≤ 5; a3+b4=–1+4=3 ≤ 7;
a4+b1=–4+9=5 > 0 [5];
Для клетки A3B1 (из тех, что не выполняется условие оптимальности) разница потенциалов наибольшая, потому для нее делаем цикл пересчета на минимальную величину отрицательных вершин: min(80, 40, 150)=40.
Переходим к следующей итерации.
| B A | 1 | 2 | 3 | 4 | a | |||||
| 200 | 200 | 140 | 180 | |||||||
| 1 | 220 | 9 | 8 | 7 | 4 | 0 | ||||
| 40 | – | 0 | + | 180 | ||||||
| 2 | 120 | 5 | 6 | 10 | 3 | –4 | ||||
| 120 | ||||||||||
| 3 | 150 | 2 | 3 | 5 | 7 | –7 | ||||
| 40 | + | 110 | – | |||||||
| 4 | 230 | 0 | 0 | 0 | 0 | –10 | ||||
| 90 | + | 140 | – | |||||||
| b | 9 | 10 | 10 | 4 | ||||||
Стоимость 4 плана перевозки:
z4 = 40 · 9+180 · 4+120 · 5+40 · 2+110 · 3+90 · 0+140 · 0 = 2090.
Для базисных клеток система потенциалов такая:
a1+b1=9; a1+b4=4;
a2+b1=5;
a3+b1=2; a3+b2=3;
a4+b2=0; a4+b3=0;
Поскольку количество переменных меньше, чем уравнений, то положим: a1=0. Проверяем условие оптимальности для свободных клеток: a + b ≤ c
a1+b2=0+10=10 > 8 [2]; a1+b3=0+10=10 > 7 [3];
a2+b2=–4+10=6 ≤ 6; a2+b3=–4+10=6 ≤ 10; a2+b4=–4+4=0 ≤ 3;
a3+b3=–7+10=3 ≤ 5; a3+b4=–7+4=–3 ≤ 7;
a4+b1=–10+9=–1 ≤ 0; a4+b4=–10+4=–6 ≤ 0;
Для клетки A1B3 (из тех, что не выполняется условие оптимальности) разница потенциалов наибольшая, потому для нее делаем цикл пересчета на минимальную величину отрицательных вершин: min(40, 110, 140)=40.
Переходим к следующей итерации.
| B A | 1 | 2 | 3 | 4 | a | |||||
| 200 | 200 | 140 | 180 | |||||||
| 1 | 220 | 9 | 8 | 7 | 4 | 0 | ||||
| 40 | 180 | |||||||||
| 2 | 120 | 5 | 6 | 10 | 3 | –1 | ||||
| 120 | ||||||||||
| 3 | 150 | 2 | 3 | 5 | 7 | –4 | ||||
| 80 | 70 | |||||||||
| 4 | 230 | 0 | 0 | 0 | 0 | –7 | ||||
| 130 | 100 | |||||||||
| b | 6 | 7 | 7 | 4 | ||||||
Стоимость 5 плана перевозки:
z5 = 40 · 7+180 · 4+120 · 5+80 · 2+70 · 3+130 · 0+100 · 0 = 1970.
Для базисных клеток система потенциалов такая:
a1+b3=7; a1+b4=4;
a2+b1=5;
a3+b1=2; a3+b2=3;
a4+b2=0; a4+b3=0;
Поскольку количество переменных меньше, чем уравнений, то положим: a1=0. Проверяем условие оптимальности для свободных клеток: a + b ≤ c
a1+b1=0+6=6 ≤ 9; a1+b2=0+7=7 ≤ 8;
a2+b2=–1+7=6 ≤ 6; a2+b3=–1+7=6 ≤ 10; a2+b4=–1+4=3 ≤ 3;
a3+b3=–4+7=3 ≤ 5; a3+b4=–4+4=0 ≤ 7;
a4+b1=–7+6=–1 ≤ 0; a4+b4=–7+4=–3 ≤ 0;
Условие оптимальности выполняется для всех клеток, следовательно последний план является оптимальным. Его стоимость составляет 1970 у.е. Следует заметить, что потребители не дополучат 230 ед. груза.
2) Метод минимальной стоимости
Найдем опорный план методом минимальной стоимости [1, c. 142].
| B A | 1 | 2 | 3 | 4 | a | |||||
| 200 | 200 | 140 | 180 | |||||||
| 1 | 220 | 9 | 8 | 7 | 4 | 0 | ||||
| 40 | 180 | |||||||||
| 2 | 120 | 5 | 6 | 10 | 3 | –1 | ||||
| 120 | ||||||||||
| 3 | 150 | 2 | 3 | 5 | 7 | –4 | ||||
| 80 | 70 | |||||||||
| 4 | 230 | 0 | 0 | 0 | 0 | –7 | ||||
| 130 | 100 | |||||||||
| b | 6 | 7 | 7 | 4 | ||||||
Стоимость начального плана перевозки:
z0 = 40 · 7+180 · 4+120 · 5+80 · 2+70 · 3+130 · 0+100 · 0 = 1970.
Для базисных клеток система потенциалов такая:
a1+b3=7; a1+b4=4;
a2+b1=5;
a3+b1=2; a3+b2=3;
a4+b2=0; a4+b3=0;
Поскольку количество переменных меньше, чем уравнений, то положим: a1=0. Проверяем условие оптимальности для свободных клеток: a + b ≤ c
a1+b1=0+6=6 ≤ 9; a1+b2=0+7=7 ≤ 8;
a2+b2=–1+7=6 ≤ 6; a2+b3=–1+7=6 ≤ 10; a2+b4=–1+4=3 ≤ 3;
a3+b3=–4+7=3 ≤ 5; a3+b4=–4+4=0 ≤ 7;
a4+b1=–7+6=–1 ≤ 0; a4+b4=–7+4=–3 ≤ 0;
Условие оптимальности выполняется для всех клеток, следовательно последний план является оптимальным. Его стоимость составляет 1970 у.е. Следует заметить, что потребители не дополучат 230 ед. груза.
Также отмечаем совпадение решений двумя методами.
Ответ: 1970.
Література
1. Акулич И. Л. Математическое программирование в примерах и задачах. М.: Высшая школа, 1986. – 319 с.
2. Костевич Л. С. Математическое программирование. Мн.: Новое знание, 2003. – 424 с.
Похожие работы
... разрабатываются методы отыскания экстремальных значений целевой функции среди множества ее возможных значений, определяемых ограничениями. Наличие ограничений делает задачи математического программирования принципиально отличными от классических задач математического анализа по отысканию экстремальных значений функции. Методы математического анализа для поиска экстремума функции в задачах ...
... рулонов, при котором все поступающие специальные заявки будут выполнены при минимальных затратах бумаги. Графический метод решения задач линейного программирования 1. Область решений линейных неравенств. Пусть задано линейное неравенство с двумя переменными и (1) Если величины и рассматривать как координаты точки плоскости, то совокупность точек ...
... вторым способом, тогда мы получим 600 заготовок первого вида, 200 – второго, 400 – третьего, 400 – четвёртого, при минимальных отходах, равных 56 м2.Экономическая сущность и математическое моделирование транспортных задач.Известны: пункты производства (А1, А2 … Ai … Аm); m – пунктов, производящих конкретную продукцию; аi – мощность i-поставщика (сколько необходимо реализовать продукции, т. е. ...
... 175 * 8 + 25 * 4 = 8085. По сравнению с исходным решением, транспортные расходы уменьшились на 175 усл.ед. (8260 – 8085 = 175). Задачи 41–50. Составить экономико-математическую модель. Найти решение задачи линейного программирования при помощи средств Excel на ПК. 48. В суточном рационе кормления крупного рогатого скота должно быть не менее 20 кормовых единиц, не менее 2000 г белков и не ...

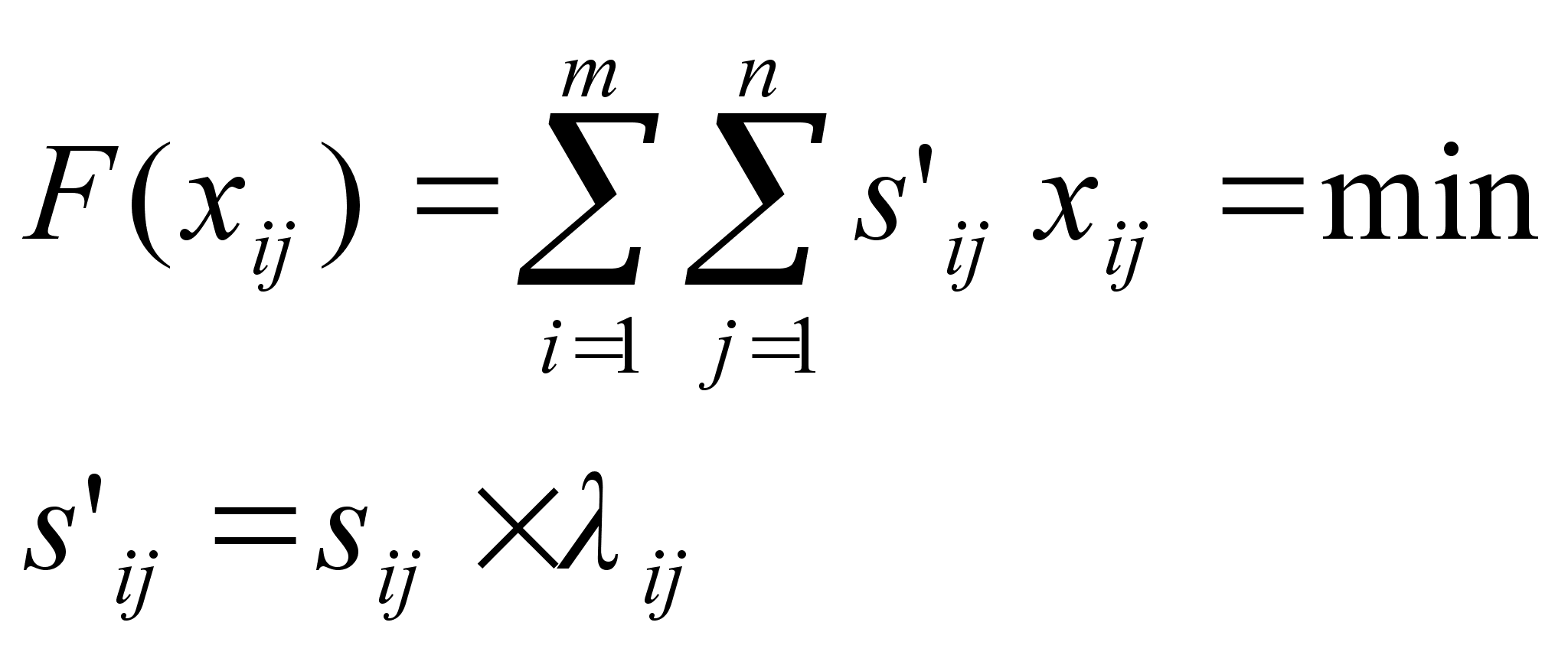
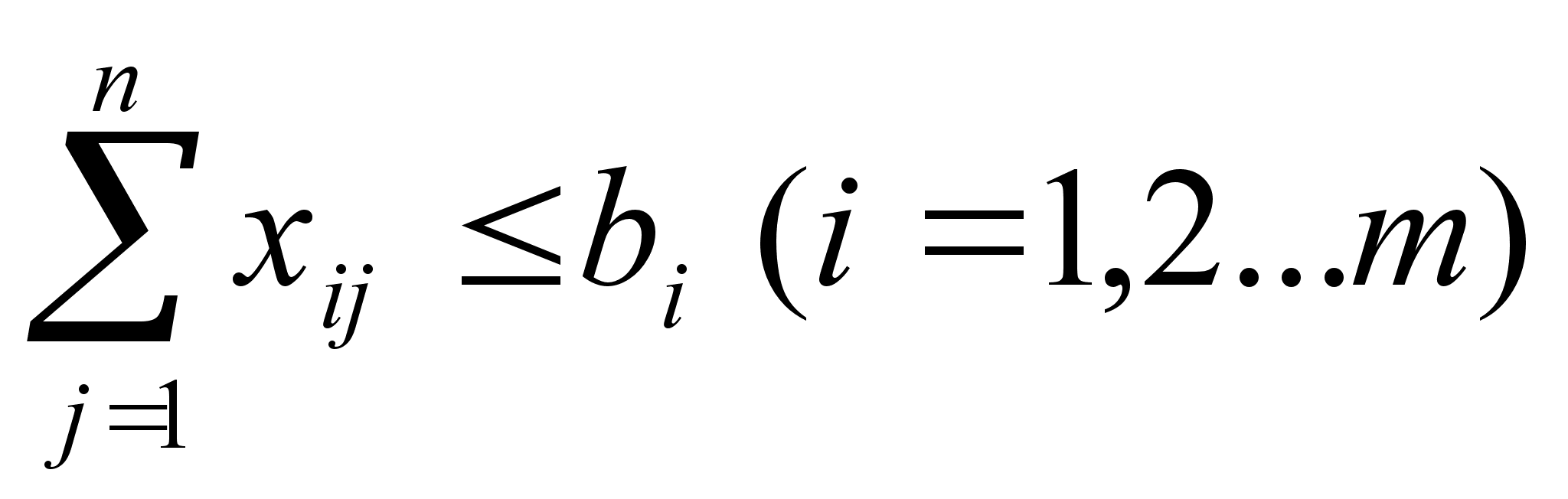
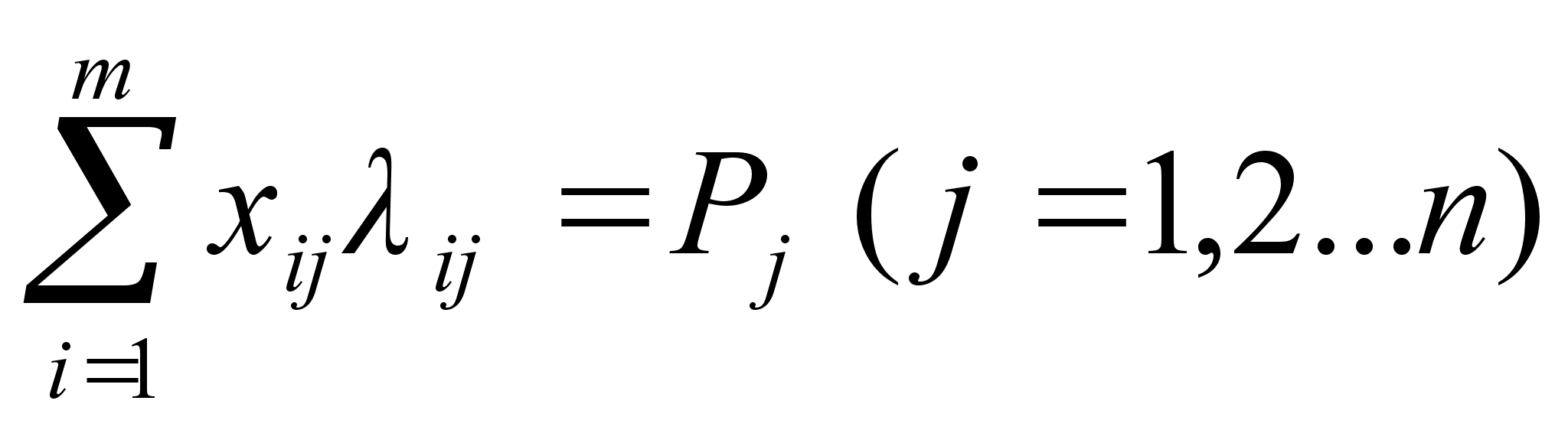
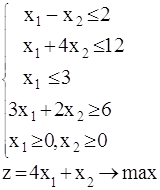

0 комментариев