Навигация
1. КОНЦЕПТУАЛЬНАЯ МОДЕЛЬ
Пусть имеется система массового обслуживания с переменным числом каналов NK, которое может принимать любое значение в диапазоне от одного до трех. Входной поток заявок - простейший, следовательно, время между соседними заявками имеет показательное распределение с известным математическим ожиданием (средним значением) Тз.ср.
Время обслуживания заявки в любом канале - величина случайная, имеющая показательное распределение с известным средним временем обслуживания Тобс.ср.
Все заявки однородны и независимы.
Правило (дисциплина) обслуживания состоит в том, что очередная заявка поступает в тот канал, который раньше других освободился. Если время ожидания начала обслуживания превышает заданную величину Тож.max, то заявка покидает систему необслуженной. Период функционирования СМО характеризуется величиной Tкон.
Таким образом, входными характеристиками модели являются: число каналов NK, среднее время между соседними заявками Tз.ср, среднее время обслуживания заявки Тобс.ср, максимально допустимое время ожидания Тож.mах, период работы системы Ткон., число случайных реализаций моделируемого процесса Np.
Выходной характеристикой модели является среднее число обслуженных заявок Nобс.ср
Выбор показателя и критерия эффективности
В качестве показателя эффективности работы системы целесообразно выбрать среднюю прибыль, определяемую по формуле
| Сcр = С1 * Nобс.ср – С2(NK), | (1) |
где С1 - чистая прибыль, полученная в результате обслуживания одной заявки;
С2(NK) - издержки обслуживания всех заявок, зависящие от числа каналов.
Разделим обе части равенства (1) на величину С1. Получим следующее выражение для расчета показателя эффективности:
|
| (2) |
где Ccр.отн - средняя относительная прибыль.
Величину С2/С1 (отношение издержек обслуживания к чистой прибыли, полученной в результате обслуживания одной заявки) будем рассматривать как функцию числа каналов.
Предположим, что возможными вариантами этой функциональной зависимости являются: а - линейная зависимость; б - возрастающая зависимость с положительной 2-й производной и в - возрастающая зависимость с отрицательной 2-й производной (рис. 1).
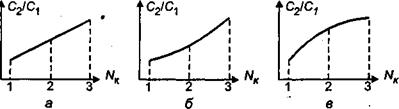
Рис.1. Зависимости отношения С2/С1, от NК : а - первый вариант; б - второй вариант; в - третий вариант
Выберем второй вариант. Примем в качестве конкретной зависимости издержек обслуживания от числа каналов следующую функцию:
|
| (3) |
Итак, для расчета показателя эффективности будем использовать зависимости (2) и (3).
В качестве критерия выбора наивыгоднейшей структуры СМО примем оптимальное число каналов, обеспечивающее максимум средней относительной прибыли:
|
| (4) |
где NK* - наивыгоднейшее число каналов.
2. СХЕМЫ АЛГОРИТМОВ МОДЕЛИ
В качестве языка программирования для разработки компьютерной модели рассматриваемого процесса выбран Visual Basic 5.0.
Общий вид (макет) стартовой формы показан на рис. 2. Видно, что она включает ряд объектов управления, среди которых имеются три командные кнопки: «Расчет», «Очистка» и «Выход». Это обстоятельство определяет структуру алгоритма процедур обработки прерываний, показанную на рис. 3.
После нажатия кнопки «Start» активизируется стартовая форма. С этого момента программа находится в режиме ожидания действий пользователя.
Цифрой 1 (рис.3) обозначено действие, заключающееся в корректировке исходных данных. Необходимые изменения вносятся в соответствующие текстовые поля.
Цифрой 2 обозначено действие, заключающееся в нажатии (с помощью мыши) кнопки «Расчет». В процедуре, связанной с этой кнопкой, оператор 3 осуществляет перевод исходных данных из символьной формы в числовую. Затем оператор 4 обращается к модулю общего назначения «Model2». Схема алгоритма этого модуля приведена на рис. 4.
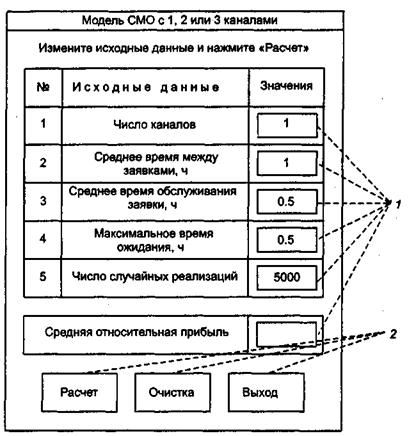
Рис. 2. Макет стартовой формы:
1 - текстовые поля; 2 - командные кнопки
После окончания работы модуля и выдачи на экран результатов моделирования работа процедуры, связанной с кнопкой «Расчет», заканчивается. Программа вновь переходит в режим ожидания действий пользователя.
Цифрой 5 на схеме (рис.3) обозначено действие пользователя, заключающееся в нажатии кнопки «Очистка». В процедуре, связанной с ней, производится очищение текстового поля для вывода результата моделирования. Затем обычно производятся изменение исходных данных и проведение новых расчетов с использованием кнопки «Расчет».
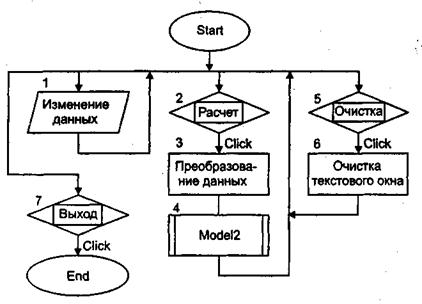
Рис.3. Схема алгоритма процедур обработки прерываний
Цифрой 7 на схеме обозначено действие пользователя, заключающееся в нажатии кнопки «Выход». В результате работа программы прекращается.
Оператор 1 на рис. 4 обнуляет глобальную переменную SNобс - суммарное число обслуженных заявок. Оператор 2 активизирует окно формы № 2 и делает неактивным окно формы № 1. Оператор 3 начинает циклический перебор случайных реализаций. Оператор 4 выводит на экран (в окно формы № 2) счетчик числа рассчитанных реализаций.
Оператор 5 в начале каждой случайной реализации обнуляет локальные переменные, к которым относятся: число заявок, поступающих в одной реализации Nz, число обслуженных заявок в каждом из трех каналов Nобс1, Nобс2, Nобс3, начальные значения времени освобождения 1-го, 2-го и 3-го каналов Tок1, Tок2 и Tок3.
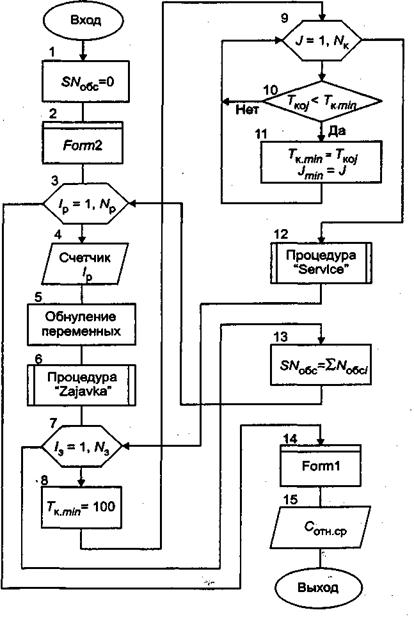
Рис.4. Схема алгоритма модуля «Model2»
Оператор 6 обращается к автономной процедуре формирования потока заявок. В результате работы этой процедуры формируется массив значений времени
[Тз(1), Тз(2), Тз(3),…, Тз(Nзi)],
где Nзi -общее число поступивших заявок для i-й случайной реализации.
Оператор 7 является началом цикла обслуживания заявок. Операторы 8, 9, 10 и 11 производят выбор номера канала, который характеризуется наименьшим значением времени освобождения от обслуживания заявки.
Оператор 12 обращается к автономной процедуре обслуживания очередной заявки. На выходе этой процедуры определяется число обслуженных заявок в выбранном канале Nобс(Jmin).
Оператор 13 служит для расчета суммарного числа обслуженных заявок по рекурсивной формуле
SNобс = SNобс + Nобс.1 + Nобс.2 + Nобс.3.
После окончания цикла случайных реализаций оператор 14 возвращает свойство активного окна форме № 1. Оператор 15 рассчитывает и выводит на экран значение выходной переменной - средней относительной прибыли по формуле
![]() .
.
Схема алгоритма процедуры формирования заявок показана на рис. 5.
Оператор 1 устанавливает на нуль модельное время Т. Оператор 2 является началом цикла формирования заявок. Оператор 3 обращается к датчику случайных чисел, который вырабатывает возможное значение случайной величины z, равномерно распределенной в интервале (0,1).
Оператор 4 определяет возможное значение случайной величины времени поступления очередной заявки при условии, что среднее время между соседними заявками равно Тз.cp. Оператор 5 проверяет условие окончания процесса формирования заявок.
Оператор 6 подсчитывает число поступивших заявок, помещает время поступления каждой заявки в специальный массив и изменяет модельное время Т.
Схема алгоритма процедуры обслуживания заявок показана на рис. 6.
Оператор 1 обнуляет время ожидания начала обслуживания заявки Tож и присваивает времени начала обслуживания Tн время поступления очередной заявки T3(J3).
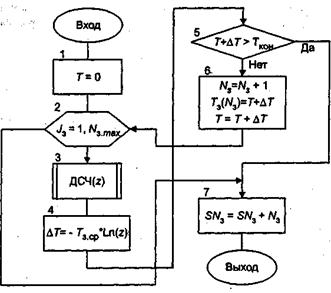
Рис.5. Схема алгоритма формирования заявок
Оператор 2 производит проверку занятости канала. Начальное значение времени освобождения канала Ткоj приравнивается нулю в главном модуле в блоке обнуления локальных переменных.
Если канал занят, то оператор 3 определяет время ожидания Tож как разность времени освобождения канала Ткоj и времени поступления заявки T3(J3). Оператор 4 проверяет условие, что время ожидания Тож превышает допустимое Тож.max. Если это условие выполняется, то управление передается на конец процедуры и заявка остается необслуженной.
Оператор 5 служит для коррекций времени начала обслуживания заявки. Оно теперь должно равняться времени освобождения канала Ткоj. Оператор 6 обращается к датчику случайных чисел с равномерным распределением в интервале (0,1), который вырабатывает возможное значение случайной величины z. Оператор 7 определяет возможное значение времени окончания обслуживания заявки Тк.
Оператор 8 проверяет условия окончания периода обслуживания, а оператор 9 фиксирует тот факт, что данный канал будет занят до конца рабочего дня. Оператор 10 увеличивает на единицу число обслуженных заявок в j-м канале и фиксирует время освобождения канала.
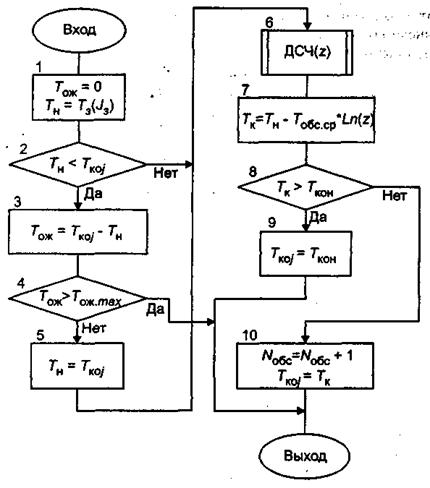
Рис. 6. Схема алгоритма процедуры обслуживания заявок
Похожие работы
... им машин. Таким образом, в отрасли вновь восстановилась система лидерства в ценах. [3.329] Монополия. Монополизм в России ¨ Основные черты монополии Монополия — наиболее яркое проявление несовершенной конкуренции. Собственно говоря, в условиях монополизации рынка само существование конкуренции может быть признано лишь с большими оговорками. Ведь конкуренция предполагает разделение ...
... значит, найденный план перевозок является оптимальным. Ответ: x21=100; x31=200; x41=200; x42=100; x52=200; x13=300; x43=500. 2.4 Решение задачи 4 Составим математическую модель поставленной задачи. Найти минимум функции f(x1,x2) При ограничениях Заменив знак функции f(x1,x2) на противоположный, перейдем к поиску максимума функции: Теперь задача приведена к стандартному виду ...
... , где - нижняя граница медианного интервала; - ширина медианного интервала; - накопленная частота интервала, предшествующего медианному; - частота медианного интервала. Рассчитаем медиану ряда распределения рабочих по размеру зарплаты (см. лекцию "Сводка и группировка статистических данных"). Медианным является интервал заработной платы 800-900 грн., поскольку его кумулятивная частота ...
... почуствовав, что внесённое ею в товар улучшение хорошо принято публикой, должна быть готова к резкому возрастанию спроса. Раздел 4. Особенности коммутантной (приспособительской) стратегии предложения товаров на рынок. Коммутантная стратегия преобладает при обычном бизнесе в местных (локальных) масштабах. Сила мелкого неспециализированного предприятия состоит в его лучшей приспособленности к ...
 ,
,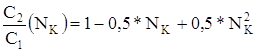 .
.




0 комментариев