Навигация
Алгоритм вычисления показателей и экономический анализ полученных результатов
1.2. Алгоритм вычисления показателей и экономический анализ полученных результатов
В качестве изучаемой системы берётся экономика условного объекта.
Исходные данные приведены в таблице 1:
Таблица 1
| a | d | f | b | MS | k | h | j | p | A | |
| 127500 | 85000 | 229500 | 0,31 | 11000 | 0,25 | 5100 | 19800 | 0,3 | 2700 | 0,51 |
По заданным в таблице 1 значениям: a, b, d, f , используя табличный редактор Excel, рассчитываем по формуле (1.13) зависимость YG = F1(r). Значения r задаём в пределах от 0 до 1,0 с шагом ∆r=0,05. Результаты вычислений представлены в таблице 2:
Таблица 2
| r | YG |
| 0 | 307971 |
| 0,05 | 291340,58 |
| 0,1 | 274710,14 |
| 0,15 | 258079,71 |
| 0,2 | 241449,28 |
| 0,25 | 224818,84 |
| 0,3 | 208188,41 |
| 0,35 | 191557,97 |
| 0,4 | 174927,54 |
| 0,45 | 158297,10 |
| 0,5 | 141666,67 |
| 0,55 | 125036,23 |
| 0,6 | 108405,80 |
| 0,65 | 91775,36 |
| 0,7 | 75144,93 |
| 0,75 | 58514,49 |
| 0,8 | 41884,06 |
| 0,85 | 25253,62 |
| 0,9 | 8623,19 |
| 0,95 | -8007,25 |
| 1 | -24637,68 |
Аналогично производим расчёты значений функции YМ = F2(r), используя формулу (1.15). Численные значения MS, h, j, k, p приведены в таблице 1.
Результаты вычислений приведены в таблице 3:
Таблица 3
r | YM |
| 0 | 78666,67 |
| 0,05 | 91866,67 |
| 0,1 | 105066,67 |
| 0,15 | 118266,67 |
| 0,2 | 131466,67 |
| 0,25 | 144666,67 |
| 0,3 | 157866,67 |
| 0,35 | 171066,67 |
| 0,4 | 184266,67 |
| 0,45 | 197466,67 |
| 0,5 | 210666,67 |
| 0,55 | 223866,67 |
| 0,6 | 237066,67 |
| 0,65 | 250266,67 |
| 0,7 | 263466,67 |
| 0,75 | 276666,67 |
| 0,8 | 289866,67 |
| 0,85 | 303066,67 |
| 0,9 | 316266,67 |
| 0,95 | 329466,67 |
| 1 | 342666,67 |
По полученным данным строим графики зависимостей YG = F1(r) и YМ = F2(r), применив «Мастер диаграмм» табличного редактора Excel (Приложение 1). По точке пересечения этих графиков находим величиныY0 и r0, определяющие равновесие на рынках денег и товаров:
| r0 | 0,4 |
| YG0 | 184266,67 |
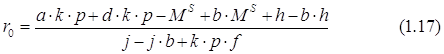 |
Исходя из условия равновесия на рынках денег и товаров, определяем аналитическим путём величину r0 по формуле:
По формуле (1.17) получаем: r0 = 0,38
Сравнивая полученное значение r0 со значением r0, найденным графическим путем, делаем вывод, что они совпадают. Подставляем значение r0 в формулы (1.13) и (1.15) и находим аналитическое значение Y0. Аналитическое значение Y0 = 180134,09. Сравнивая его с Y0, полученным графическим путем, делаем вывод, что они практически совпадают.
Используя производственную функцию вида:
Y=A*L, (1.18)
находим величину L0 по формуле:
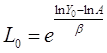 (1.19)
(1.19)
Значения величин A и берём из таблицы 1. По формуле (1.19) получаем:
L0 = 3775,08.
Рассчитываем по формуле (1.18) производственную функцию Y = F3(L) и строим её график, используя возможности табличного редактора Excel (Приложение 2). Результаты вычислений приведены в таблице 4:
Таблица 4
| L | Y |
| 0 | 0 |
| 1000 | 87138,73 |
| 2000 | 124953,04 |
| 3000 | 154281,66 |
| 4000 | 179177,07 |
| 5000 | 201222,08 |
| 6000 | 221232,99 |
| 7000 | 239696,79 |
| 8000 | 256931,9 |
| 9000 | 273160,15 |
| 10000 | 288543,46 |
| 11000 | 303204,36 |
| 12000 | 317238,21 |
| 13000 | 330721,01 |
| 14000 | 343714,47 |
| 15000 | 356269,54 |
| 16000 | 368428,85 |
| 17000 | 380228,51 |
| 18000 | 391699,43 |
| 19000 | 402868,32 |
| 20000 | 413758,41 |
По значению Y0 находим графическим путем величину L0. Графическое значение L0 = 3775,08. Сравнивая его со значением L0, полученным аналитически, делаем вывод, что они совпадают.
ГЛАВА 2. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ МОДЕЛИ
2.1. Постановка задачиВ данной работе необходимо определить в простой кейнсианской модели формирования доходов параметры уравнения функции потребления. Исходная система уравнений имеет вид:
Ct = a + b*Yt + ut ; (2.1)
Yt = Ct + It, (2.2)
где t – индекс, указывающий на то, что уравнения (2.1), (2.2) являются системой одновременных уравнений для моментов времени t1-tn;
ut – случайная составляющая;
Ct, Yt – функции потребления и дохода, соответственно являющиеся эндогенными переменными;
It – экзогенно заданная функция, отражающая инвестиционный спрос.
Переменные Ct и Yt являются эндогенными. Эндогенной считается та переменная, значение которой определяется внутри уравнения регрессии, внутри модели. В качестве экзогенной переменной в данной задаче выступают инвестиции It. Экзогенной является та переменная, значение которой определяется вне уравнения регрессии, вне модели и поэтому берется как заданная.
Параметры уравнения регрессии необходимо определить двумя способами:
· косвенным методом наименьших квадратов;
· прямым методом наименьших квадратов.
2.2. Определение параметров уравнения регрессии с использованием КМНК
Исходные значения величин Ct и It представлены в таблице 5:
Таблица 5
| t | Ct | It |
| 1 | 220063 | 85000 |
| 2 | 231828 | 78115 |
| 3 | 207359 | 71230 |
| 4 | 218337 | 64345 |
| 5 | 207851 | 57460 |
| 6 | 202994 | 50575 |
| 7 | 195524 | 43690 |
| 8 | 203944 | 36805 |
| 9 | 201672 | 29920 |
| 10 | 186648 | 23035 |
| 11 | 187864 | 16150 |
| 12 | 185659 | 9265 |
| 13 | 193932 | 2380 |
| 14 | 187232 | 85 |
Методом наименьших квадратов (МНК) из уравнения (2.1) найти параметры a и b невозможно, так как оценки будут смещёнными. В связи с этим необходимо использовать косвенный метод наименьших квадратов (КМНК).
Для этого эндогенные переменные Ct, Yt выражаем через экзогенную переменную It. С этой целью подставляем выражение (2.1) в (2.2):
Yt = a+b*Yt + ut +It, (2.3)
отсюда получаем:
![]() (2.4)
(2.4)
Подставляем выражение (2.4) в уравнение (2.1) и получаем:
![]() (2.5)
(2.5)
Данное уравнение не содержит в правой части эндогенных переменных, а имеет только экзогенную переменную в виде It (инвестиций). Экзогенная переменная не коррелирует со случайной составляющей ut и, следовательно, параметры этого уравнения могут быть найдены с помощью МНК.
Представим это уравнение в следующем виде:
![]() (2.6)
(2.6)
где
![]()
![]()
![]() (2.7)
(2.7)
b1- несмещенная оценка b*.
Для этих целей применяем имеющийся в табличном редакторе Excel пакет прикладных программ, реализующий определение параметров уравнения регрессии методом наименьших квадратов. Активизация этого метода производится командами: «Сервис» – «Анализ данных» – «Регрессия».
| a1 | b1 |
| 184280,63 | 0,44 |
После определения значений a1 и b1 необходимо определить несмещенные оценки величин a и b, использовав соотношения:
![]()
![]() , (2.9)
, (2.9)
где a", b" – соответственно несмещенные оценки a, b.
Сами значения величин a", b" определяем по формулам:
![]()
![]() (2.10)
(2.10)
| a" | b" |
| 127811,09 | 0,31 |
Использовав найденные значения a" и b", записываем уравнение функции потребления (2.1):
C(t)= 127811,09 + 0,31*Yt+ut.
Сравниваем найденные по формуле (2.10) значения a" и b" с величинами a и b, заданными в таблице 1 (aтабл. = 127500, bтабл. = 0,31) и рассчитываем проценты несовпадения данных величин по формулам:
![]()
![]() (2.11)
(2.11)
![]() ,
,
![]() .
.
Похожие работы
... , что в современной экономике главной движущей силой ее развития является свободное предпринимательство. Это обстоятельство и позволяет считать Й. Шумпетера представителем неолиберализма. 3.2 Развитие теории и практики регулирования рыночной экономики в период «великой депрессии» В 30-тые годы XX века кризисные процессы в экономике и экономической теории Запада достигли небывалой остроты. ...
... а экономико-административная (с ударением на первом слове) модель должна стать приоритетом. И изобретать тут ничего нового не приходится. Среди главных и апробированных инструментов регулирования рыночной экономики следующие: финансово-кредитная система с совершенной налоговой, эмиссионной и таможенно-пошлинной политикой, финансированием, кредитом, стратегией и тактикой процентных ставок; ...
... осуществляются, не создают адекватных условий для предпринимательства, поэтому и механизм мотивации к труду и предпринимательству полностью еще не включен. 4. Противоречия регулирования отношений собственности в России 4.1 Разгосударствление экономики при различных моделях реформирования Огосударствление всей общественной жизни означает, что государство занимает монопольное положение, а ...
... государства - везде где необходимо. Необходимость воздействия государства на экономическую сферу и степень этого воздействия зависят от чрезвычайно большого количества факторов: как от состояния рыночной экономики в целом, так и от стратегии государственного экономического развития. Основные причины отказов рынка и государственного вмешательства сводятся к следующему: 1. Монопольная власть. ...
0 комментариев