Навигация
Стохастические модели управления запасами с фиксированным временем задержки поставок
2.1.5 Стохастические модели управления запасами с фиксированным временем задержки поставок
В рассмотренных выше идеализированных моделях управления запасами предполагалось, что пополнение запаса происходит практически мгновенно. Однако в ряде задач время задержки поставок может оказаться настолько значительным, что его необходимо учитывать в модели.
Пусть за время задержек поставок q уже заказаны n партий по одной в каждый из n периодов продолжительностью Т = q/n.
Обозначим:
sнз — первоначальный уровень запаса (к началу первого периода);
si — запас за i-й период;
ri — спрос за i-й период;
qi — пополнение запаса за i-й период.
Тогда к концу n-го периода на склад поступит Sqi единиц продукта, а будет израсходовано Sri единиц, т.е.
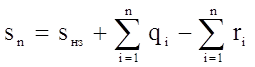 , (2.23)
, (2.23)
или
sn = s - r, (2.24)
гдеs - запас за i - й период и определяется по формуле:
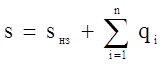 ; (2.25)
; (2.25)
где r - спрос за i - й период. Он равен:
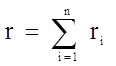 (2.26)
(2.26)
Требуется найти оптимальный объем партии заказа, который необходимо сделать за последний n-й период, предшествующий поступлению сделанного ранее заказа. Математическое ожидание суммарных затрат в этом случае определяется по формуле (2.18), а оптимальный запас s находится по формуле:
F(s0) < p < F(s0 + 1), (2.27)
Найдя оптимальный запас s0 и зная q1, q2,…, qn-1, можно вычислить qn по формуле (2.28) [10], т.е.
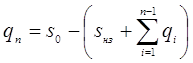 (2.28)
(2.28)
2.2 Обоснование выбора модели управления запасами
Модели управления запасами специфичны, в большинстве случаев они не могут в точности отражать какую-то конкретную ситуацию. И, тем не менее, при планировании хозяйственной деятельности предприятия было бы неверным пренебрегать любыми возможностями использования математического аппарата для построения моделей управления запасами.
Деятельность Змиевской ТЭС осуществляется в таких направлениях: производство и продажа электрической и тепловой энергии, снабжение электроэнергии, коммерческо-посредническая и внешнеэкономическая деятельность, предоставление бытовых услуг. Для этого предприятие закупает уголь у Донецких и Луганских поставщиков с запасом, который хранится на складе.
В процессе деятельности спрос на уголь подвержен влиянию фактора сезонности, то есть существуют периоды, когда спрос выше запаса и угля на складе оказывается недостаточно. В этом случае предприятие обращается к поставщику, однако на его доставку требуется определенное время, в течении которого предприятие несет значительные убытки. Возможен и такой вариант, когда необходимости в запасе угля нет и предприятие несет убыток от его приобретения и хранения, не пользующегося спросом на данный момент времени.
Для расчета оптимального запаса были взяты данные по расходу угля за каждый день в течение всего года.
Анализ статистических данных показал, что величина потребления угля каждый месяц различна и носит случайный, но циклический характер. Этот факт указывает на то, что для расчета оптимального запаса продукции необходимо использовать стохастическую модель управления запасами.
2.3 Расчет оптимального запаса
2.3.1 Построение таблиц потребления угля
Построим зависимости потребления угля по дням, по месяцам, а также зависимость потребления, опираясь на данные таблицы 1.4.
Для построения зависимости потребления угля по дням, найдем среднее значения потребления по каждому дню. Для этого просуммируем потребление угля по каждому номеру дня в течение всего года, и разделим это значение на количество дней. Таким образом, мы получим диапазон потребления угля с 1 по 7 день, который показывает среднее значения потребления. Полученный график представлен на рисунке 2.5
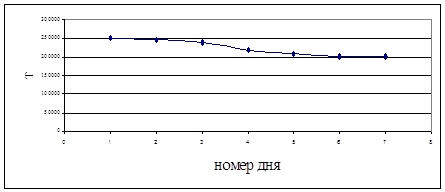
Рисунок 2.5 — Потребление угля Змиевской ТЭС по дням
Для построения зависимости потребления угля по месяцам, найдем среднее значение потребления угля за каждый месяц, в течение года. Получим диапазон потребления угля с 1 по 12 месяц. Полученный график представлен на рисунке 2.6
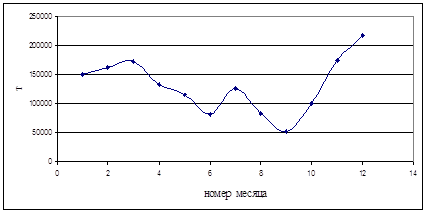
Рисунок 2.6 — Потребление угля Змиевской ТЭС по месяцам
Из рисунков мы видим, что все графики — это периодические процессы.
Также мы видим ярко выраженную циклическую зависимость. Следовательно, функция распределения также должна иметь зависимость от дня, месяца и потребления.
На основании таблицы 1.4 создадим таблицу потребления угля в месяц по каждому дню
Таблица 2.1 — Потребления угля в месяц по каждому дню
| Месяц | № дня | Потребление угля по дням | ||||
| Январь | 1 | 7788 | 1789 | 4958 | 5869 | 5278 |
| 2 | 7559 | 2256 | 5849 | 6263 | 3422 | |
| 3 | 5702 | 587 | 6658 | 8794 | 4151 | |
| 4 | 7338 | 4201 | 6249 | 6991 | ||
| 5 | 6998 | 3950 | 5286 | 5519 | ||
| 6 | 2650 | 3385 | 5904 | 2022 | ||
| 7 | 2036 | 4012 | 5544 | 2449 | ||
| Февраль | 1 | 3286 | 4388 | 5229 | 5350 | 7156 |
| 2 | 5420 | 5552 | 5934 | 6768 | ||
| 3 | 5568 | 3985 | 6218 | 6209 | ||
| 4 | 8022 | 4289 | 5306 | 6224 | ||
| 5 | 5130 | 4241 | 5544 | 5722 | ||
| 6 | 5556 | 6163 | 5624 | 5035 | ||
| 7 | 5855 | 5577 | 5316 | 7361 | ||
| Март | 1 | 5718 | 4232 | 4560 | 5087 | 7604 |
| 2 | 5339 | 6898 | 3980 | 6578 | 7217 | |
| 3 | 4813 | 5271 | 6026 | 5348 | 6663 | |
| 4 | 4790 | 5955 | 6132 | 6016 | ||
| 5 | 5204 | 4938 | 5524 | 5691 | ||
| 6 | 5215 | 3798 | 5838 | 5201 | ||
| 7 | 7357 | 4564 | 5586 | 5897 | ||
Месяц | № дня | Потребление угля по дням | ||||
| Апрель | 1 | 6418 | 3893 | 3938 | 3815 | 3256 |
| 2 | 8519 | 3636 | 2820 | 3560 | 4865 | |
| 3 | 6656 | 3945 | 4529 | 3868 | ||
| 4 | 6970 | 7983 | 3199 | 3451 | ||
| 5 | 4683 | 4221 | 4397 | 3315 | ||
| 6 | 3675 | 3775 | 3998 | 4904 | ||
| 7 | 4152 | 3525 | 3380 | 2901 | ||
| Май | 1 | 4037 | 2615 | 4241 | 1529 | 3131 |
| 2 | 4135 | 3507 | 4478 | 1647 | 4425 | |
| 3 | 3865 | 4001 | 4146 | 2664 | 3519 | |
| 4 | 4368 | 3974 | 4104 | 3666 | ||
| 5 | 3902 | 3543 | 4782 | 4239 | ||
| 6 | 4280 | 4357 | 3547 | 4981 | ||
| 7 | 4588 | 4010 | 1882 | 3420 | ||
| Июнь | 1 | 3411 | 2937 | 3154 | 2301 | 1471 |
| 2 | 438 | 3528 | 4581 | 2627 | 263 | |
| 3 | 2157 | 3290 | 4354 | 2641 | ||
| 4 | 2028 | 4005 | 2742 | 925 | ||
| 5 | 3747 | 2552 | 3019 | 367 | ||
| 6 | 2946 | 3908 | 3810 | 1798 | ||
| 7 | 3113 | 2818 | 3589 | 2700 | ||
| Месяц | № дня | Потребление угля по дням | ||||
| Июль | 1 | 1469 | 4708 | 4905 | 3855 | 2859 |
| 2 | 1256 | 3416 | 4211 | 1750 | 4358 | |
| 3 | 442 | 5541 | 4807 | 2321 | 5404 | |
| 4 | 6978 | 4651 | 4225 | 2416 | ||
| 5 | 7532 | 5790 | 4628 | 1954 | ||
| 6 | 7700 | 4076 | 4610 | 2953 | ||
| 7 | 6385 | 4948 | 4050 | 1964 | ||
| Август | 1 | 4806 | 4895 | 1964 | 3695 | 1569 |
| 2 | 637 | 4774 | 1456 | 3556 | 1491 | |
| 3 | 1632 | 3681 | 1259 | 2254 | 1098 | |
| 4 | 499 | 5216 | 2556 | 1569 | ||
| 5 | 4116 | 3380 | 3256 | 1988 | ||
| 6 | 4013 | 3245 | 4562 | 1887 | ||
| 7 | 4200 | 1125 | 1168 | 2564 | ||
| Сентябрь | 1 | 1490 | 3636 | 1667 | 2597 | 503 |
| 2 | 1744 | 2566 | 1288 | 1698 | 503 | |
| 3 | 1193 | 4632 | 2561 | 329 | ||
| 4 | 624 | 546 | 2143 | 2157 | ||
| 5 | 1168 | 1945 | 2125 | 1147 | ||
| 6 | 1168 | 1839 | 589 | 1484 | ||
| 7 | 2564 | 250 | 4563 | 1092 | ||
| Месяц | № дня | Потребление угля по дням | ||||
| Октябрь | 1 | 1456 | 987 | 2047 | 3927 | 4219 |
| 2 | 800 | 1546 | 3571 | 3697 | 3482 | |
| 3 | 498 | 4707 | 2964 | 6494 | 4972 | |
| 4 | 564 | 4519 | 3045 | 5573 | ||
| 5 | 370 | 5734 | 3712 | 4672 | ||
| 6 | 531 | 4433 | 2873 | 5544 | ||
| 7 | 333 | 3209 | 4442 | 5077 | ||
| Ноябрь | 1 | 4004 | 4841 | 5463 | 8156 | 8557 |
| 2 | 4213 | 5992 | 5047 | 7328 | 8279 | |
| 3 | 5327 | 4437 | 4859 | 7677 | ||
| 4 | 4311 | 4927 | 5518 | 8165 | ||
| 5 | 4074 | 4176 | 7155 | 7641 | ||
| 6 | 3667 | 4358 | 6160 | 7469 | ||
| 7 | 3347 | 4857 | 6520 | 8119 | ||
|
Декабрь | 1 | 8449 | 9738 | 6204 | 6020 | 4519 |
| 2 | 7394 | 9059 | 8781 | 4926 | 4660 | |
| 3 | 9084 | 9448 | 6161 | 6504 | 4235 | |
| 4 | 8072 | 8720 | 7238 | 5709 | ||
| 5 | 7220 | 8276 | 4413 | 6067 | ||
| 6 | 7947 | 8659 | 5723 | 4515 | ||
| 7 | 7414 | 9239 | 6421 | 6497 | ||
2.3.2 Определение экспериментального значения функции распределения
Весь диапазон потребления угля разобьем на три интервала и определим относительную частоту попадания потребления угля в тот или иной интервал, а также сумму частот для каждого интервала.
Конечные данные приведены в таблице 2.2
Таблица 2.2 — Относительная частота попадания потребления угля в интервал
| Месяц | День | Относительные значения | Сумма частот | |||||
| Интервал | 250-3412 | 3413 – 6575 | 6576 – 9738 | 1 | 2 | 3 | 4 | |
| Январь | 1 | 0,2 | 0,6 | 0,2 | 0 | 0,2 | 0,8 | 1 |
| 2 | 0,2 | 0,6 | 0,2 | 0 | 0,2 | 0,8 | 1 | |
| 3 | 0,2 | 0,4 | 0,4 | 0 | 0,2 | 0,6 | 1 | |
| 4 | 0 | 0,5 | 0,5 | 0 | 0 | 0,5 | 1 | |
| 5 | 0 | 0,75 | 0,25 | 0 | 0 | 0,8 | 1 | |
| 6 | 0,5 | 0,5 | 0 | 0 | 0,5 | 1 | 1 | |
| 7 | 0,5 | 0,5 | 0 | 0 | 0,5 | 1 | 1 | |
| Февраль | 1 | 0 | 0,8 | 0,2 | 0 | 0 | 0,8 | 1 |
| 2 | 0 | 0,75 | 0,25 | 0 | 0 | 0,8 | 1 | |
| 3 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | |
| 4 | 0 | 0,75 | 0,25 | 0 | 0 | 0,8 | 1 | |
| 5 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | |
| 6 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | |
| 7 | 0 | 0,75 | 0,25 | 0 | 0 | 0,8 | 1 | |
| Месяц | День | Относительные значения | Сумма частот | |||||
| Интервал | 250-3412 | 3413 – 6575 | 6576 – 9738 | 1 | 2 | 3 | 4 | |
| Март | 1 | 0 | 0,8 | 0,2 | 0 | 0 | 0,8 | 1 |
| 2 | 0 | 0,4 | 0,6 | 0 | 0 | 0,4 | 1 | |
| 3 | 0 | 0,8 | 0 | 0 | 0 | 0,8 | 1 | |
| 4 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | |
| 5 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | |
| 6 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | |
| 7 | 0 | 0,75 | 0,25 | 0 | 0 | 0,8 | 1 | |
| Апрель | 1 | 0 | 0,8 | 0,2 | 0 | 0 | 0,8 | 1 |
| 2 | 0,2 | 0,6 | 0,2 | 0 | 0,2 | 0,8 | 1 | |
| 3 | 0 | 0,75 | 0,25 | 0 | 0 | 0,8 | 1 | |
| 4 | 0 | 0,5 | 1 | 0 | 0 | 0,5 | 1 | |
| 5 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | |
| 6 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | |
| 7 | 0,25 | 0,75 | 0 | 0 | 0,25 | 1 | 1 | |
| Май | 1 | 0,6 | 0,4 | 0 | 0 | 0,6 | 1 | 1 |
| 2 | 0,2 | 0,8 | 0 | 0 | 0,2 | 1 | 1 | |
| 3 | 0,2 | 0,8 | 0 | 0 | 0,2 | 1 | 1 | |
| 4 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | |
| 5 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | |
| 6 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | |
| 7 | 0,25 | 0,75 | 0 | 0 | 0,25 | 1 | 1 | |
| Месяц | День | Относительные значения | Сумма частот | |||||
| Интервал | 250-3412 | 3413 – 6575 | 6576 – 9738 | 1 | 2 | 3 | 4 | |
| Июнь | 1 | 0,6 | 0,4 | 0 | 0 | 0,6 | 1 | 1 |
| 2 | 0,6 | 0,4 | 0 | 0 | 0,6 | 1 | 1 | |
| 3 | 0,5 | 0,5 | 0 | 0 | 0,5 | 1 | 1 | |
| 4 | 0,75 | 0,25 | 0 | 0 | 0,75 | 1 | 1 | |
| 5 | 0,75 | 0,25 | 0 | 0 | 0,75 | 1 | 1 | |
| 6 | 0,5 | 0,5 | 0 | 0 | 0,5 | 1 | 1 | |
| 7 | 0,75 | 0,25 | 0 | 0 | 0,75 | 1 | 1 | |
| Июль | 1 | 0,4 | 0,6 | 0 | 0 | 0,4 | 1 | 1 |
| 2 | 0,4 | 0,6 | 0 | 0 | 0,4 | 1 | 1 | |
| 3 | 0,4 | 0,6 | 0 | 0 | 0,4 | 1 | 1 | |
| 4 | 0,25 | 0,5 | 0,25 | 0 | 0,25 | 0,8 | 1 | |
| 5 | 0,25 | 0,5 | 0,25 | 0 | 0,25 | 0,8 | 1 | |
| 6 | 0,25 | 0,5 | 0,25 | 0 | 0,25 | 0,8 | 1 | |
| 7 | 0,25 | 0,5 | 0,25 | 0 | 0,25 | 0,8 | 1 | |
| Август | 1 | 0,4 | 0,6 | 0 | 0 | 0,4 | 1 | 1 |
| 2 | 0,6 | 0,4 | 0 | 0 | 0,6 | 1 | 1 | |
| 3 | 0,6 | 0,4 | 0 | 0 | 0,6 | 1 | 1 | |
| 4 | 0,75 | 0,5 | 0 | 0 | 0,75 | 1,3 | 1 | |
| 5 | 0,25 | 0,75 | 0 | 0 | 0,25 | 1 | 1 | |
| 6 | 0,25 | 0,75 | 0 | 0 | 0,25 | 1 | 1 | |
| 7 | 0,75 | 0,25 | 0 | 0 | 0,75 | 1 | 1 | |
| Сентябрь | 1 | 0,8 | 0,2 | 0 | 0 | 0,8 | 1 | 1 |
| 2 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | |
| Месяц | День | Относительные значения | Сумма частот | |||||
| Интервал | 250-3412 | 3413 – 6575 | 6576 – 9738 | 1 | 2 | 3 | 4 | |
| Сентябрь | 3 | 0,75 | 0,25 | 0 | 0 | 0,75 | 1 | 1 |
| 4 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | |
| 5 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | |
| 6 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | |
| 7 | 0,75 | 0,25 | 0 | 0 | 0,75 | 1 | 1 | |
| Октябрь | 1 | 0,6 | 0,4 | 0 | 0 | 0,6 | 1 | 1 |
| 2 | 0,4 | 0,6 | 0 | 0 | 0,4 | 1 | 1 | |
| 3 | 0,4 | 0,6 | 0,2 | 0 | 0,4 | 1 | 1 | |
| 4 | 0,5 | 0,5 | 0 | 0 | 0,5 | 1 | 1 | |
| 5 | 0,25 | 0,75 | 0 | 0 | 0,25 | 1 | 1 | |
| 6 | 0,5 | 0,5 | 0 | 0 | 0,5 | 1 | 1 | |
| 7 | 0,25 | 0,75 | 0 | 0 | 0,25 | 1 | 1 | |
| Ноябрь | 1 | 0 | 0,6 | 0,4 | 0 | 0 | 0,6 | 1 |
| 2 | 0 | 0,6 | 0,4 | 0 | 0 | 0,6 | 1 | |
| 3 | 0 | 0,75 | 0,25 | 0 | 0 | 0,8 | 1 | |
| 4 | 0 | 0,75 | 0,25 | 0 | 0 | 0,8 | 1 | |
| 5 | 0 | 0,5 | 0,5 | 0 | 0 | 0,5 | 1 | |
| 6 | 0 | 0,75 | 0,25 | 0 | 0 | 0,8 | 1 | |
| 7 | 0 | 0,5 | 0,5 | 0 | 0 | 0,5 | 1 | |
| Декабрь | 1 | 0 | 0,4 | 0,6 | 0 | 0 | 0,4 | 1 |
| 2 | 0 | 0,4 | 0,6 | 0 | 0 | 0,4 | 1 | |
| 3 | 0 | 0,4 | 0,6 | 0 | 0 | 0,4 | 1 | |
| 4 | 0 | 0,5 | 0,75 | 0 | 0 | 0,5 | 1 | |
| 5 | 0 | 0,5 | 0,5 | 0 | 0 | 0,5 | 1 | |
| 6 | 0 | 0,5 | 0,5 | 0 | 0 | 0,5 | 1 | |
| 7 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | |
Для каждого интервала найдем середину и для каждого дня определим F(x) — экспериментальную функцию распределения.
Полученные данные приведены в таблице 1 приложения А.
Для каждого значения середины интервала определим среднее значение экспериментальной функции распределения F(x). Получим результативные данные, приведенные в таблице А.1 приложения А
Таблица 2.3 — Среднее значение экспериментальной функции распределения
| Середина интервала | Среднее значение F(X) |
| 125 | 0 |
| 1831 | 0,27 |
| 4994 | 0,84 |
| 8157 | 1 |
По полученным данным построим график экспериментального значения функции распределения потребления угля.
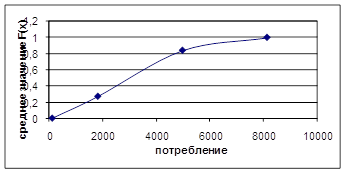
Рисунок 2.7 — Экспериментальное значение функции распределения потребления угля Змиевской ТЭС
Похожие работы
... которую в пределах инвестиционных обязательств и в контексте государственной энергетической политики постепенно могли бы реализовать частные стратегические инвесторы. 2.3. Приватизация и приток инвестиций в тепловую энергетику Украины. На основании вышеизложенного следует отметить, что для приватизации украинской теплоэнергетики существуют два весомых основания: - потребность в более ...
... в управление Минэнерго Украины с последующим созданием в первом квартале 2000 г. государственной акционерной энергетической компании; усилить ответственность руководителей всех уровней за обеспечение оплаты за энергоресурсы, что даст возможность обеспечить выплату текущей заработной платы, соответствующие платежи в бюджет и, что самое главное, оплату топлива; урегулировать вопрос покрытия ...
... биогеохимический кругооборот. В социально-экономических системах около 90% материальных ресурсов переходит в отходы, а основное количество энергии используется в производстве и потреблении. Поэтому главной задачей промышленной экологии является нахождение путей для рационального использования природных ресурсов, предотвращения их исчерпания, деградации и загрязнения окружающей среды, а в конечном ...
... Для улучшенного внедрения экологически чистых энергосберегающих технологий была разработана и утверждена согласно Постановлению Совета Министров Крыма от 14 02.94 г, №26 «Комплексная научно-техническая программа развития нетрадиционных возобновляемых источников энергии в Крыму до 2000 г.». На настоящий момент эта программа из-за отсутствия достаточного финансирования реализована частично и требует ...
0 комментариев