Навигация
Определение производительности второго цикла обработки деталей;
1. Определение производительности второго цикла обработки деталей;
2. При каком условии возможно повышение загрузки второго станка и снижение уровня задела на втором цикле обработки;
Идентификация реальных объектов
На этом этапе осуществляется определение основных элементов реальной системы, и привязка их к образным понятиям модели с дальнейшим конкретизированием и конвертированием в математическое представление на стадии расширения алгоритма программной реализации.
Для начала определим, что это вообще берется за понятие системы. Исходя из поставленной задачи, под системой подразумевается автоматизированный конвейер обработки деталей в машинном цехе, воздействие на систему с внешней среды не осуществляется, а внутреннее производится непосредственно над деталями (первичная и вторичная обработка) и станками (уровень загрузки и производительности).
Далее определим входные и выходные элементы системы, для модели это будет входная и выходная информация. За входные элементы примем детали, а точнее количество этих деталей. За выходные – производительность станков на втором уровне обработки (я не принимаю уровень загрузки сборщика брака, т.к. это можно определить по производительности).
Так же можно сразу разбить систему на две подсистемы (это в дальнейшем упростит программную реализацию): систему первичной обработки деталей и систему вторичной обработки брака. Так как известно, что бракованные детали не могут обрабатываться дважды нет необходимости в дальнейшем дроблении.
Выбор вида моделей
Виды моделей можно классифицировать следующим способом:
![]()
![]() детерминированное стохастическое
детерминированное стохастическое
![]()
![]() статическое динамическое
статическое динамическое
![]()
![]() дискретное дискретно-непрерывное непрерывное
дискретное дискретно-непрерывное непрерывное
![]()
![]() мысленное (абстрактное) реальное (материальное)
мысленное (абстрактное) реальное (материальное)
![]()
наглядное, символическое, математическое, натурное физическое
В зависимости от характера изучаемых процессов в системе S все виды моделирования могут быть разделены на: детерминированные и стохастические; статические и динамические; дискретные, непрерывные и дискретно- непрерывные.
Детерминированное моделирование отображает детерминированные процессы, то есть процессы, в которых предвидится отсутствие всяких случайных влияний.
Стохастическое моделирование отображает вероятностные процессы и случаи. Анализируется ряд реализаций случайного процесса и оцениваются средние характеристики, то есть набор однородных реализаций.
Статическое моделирование описывает поведение объекта в данный момент времени.
Динамическое моделирование отображает поведение объекта во времени.
Дискретное моделирование отображает дискретные процессы, непрерывное моделирование - непрерывные процессы, дискретно-непрерывное моделирование - оба процесса.
В зависимости от формы представления объекта (системы S) выделяют: вымышленные и реальные.
Вымышленное (абстрактное) моделирование - когда невозможно или дорогое материальное создание (модели микромира). Делится на:
v наглядное;
v символическое;
v материальное.
Наглядное моделирование - на базе представления человека об объекте создаются гипотетические модели, аналоги и макеты. Гипотетическое моделирование - выбирается гипотеза о реальном объекте, гипотеза, которая отображает уровень знаний об объекте, когда знаний не хватает для формализации. Аналоговое моделирование использует аналогии разных уровней (полная, неполная, приблизительная). Макетирование - в основе выполненного макета лежит аналогия причинно-наследственных связей.
Символическое моделирование - искусственный процесс создания логического объекта-заместителя реального с помощью системы знаков и символов. Знаковое моделирование - вводятся знаки, условные обозначения отдельных понятий, составляются из знаков слова и предложения; операции объединения, пересечения и дополнения теории множеств дают описание объекта.
Языковое моделирование - в основе лежит словарь однозначных понятий.
Математическое моделирование - замена реального объекта математическим. Делится на аналитическое, имитационное и комбинированное.
Аналитическое моделирование - процессы функционирования элементов системы записываются в виде некоторых функциональных соотношений (алгебраических, интегро-дифференциальных, конечно-разностных и т.п.) или логических условий. Аналитическая модель может быть исследована следующими методами:
v аналитическими, когда хотят получить в общем виде явные зависимости для искомых характеристик;
v численным, когда, не умея решить уравнение в общем виде, получают числовые результаты при конкретных исходных данных;
v качественный, когда не умея решить уравнение, находят некоторые свойства решений (например, стойкость и др.).
Аналитический метод связывает явной зависимостью исходные данные с искомыми результатами. Это возможно для сравнительно простых систем.
Численные методы позволяют исследовать более широкий класс систем. Они эффективны при использовании ЭВМ. Для построения аналитических моделей существует мощный математический аппарат - алгебра, функциональный анализ, разностные уравнения, теория вероятности, математическая статистика, теория массового обслуживания и т.д.
Имитационное моделирование используется, когда для описания СС недостаточно аналитического моделирования. В имитационной модели поведение компонент сложной системы (СС) описывается набором алгоритмов, которые затем реализуют ситуации, которые возникают в реальной системе. Алгоритмы, которые модулируют по исходным данным (сходное состояние СС) и фактическим значением параметров СС позволяют отобразить явления в S и получить информацию о возможном поведении СС. На основе этой информации исследователь может принять соответствующее решение. Имитационная модель (ИМ) СС рекомендуется в следующих случаях :
1) нет законченной постановки задачи исследования и идет процесс познания объекта моделирования. ИМ - способ изучения явления.
2) математические средства аналитического моделирования сложные и громоздкие и ИМ дает наиболее простой способ.
3) кроме оценки влияния параметров СС необходимо наблюдать поведение компонент СС некоторый период.
4) ИМ - единственный способ исследования СС, то есть невозможны наблюдения в реальных условиях за объектом.
5) необходимо контролировать протекание процессов в СС, уменьшая и ускоряя скорость их протекания в ходе имитации.
6) при подготовке специалистов и освоении новой техники.
7) изучение новых ситуаций в СС, проверка новых стратегий и принятие решений перед проведением экспериментов на реальной S.
8) предвиденье узких мест и трудностей в поведении СС при введении новых компонент.
ИМ - наиболее распространенный метод анализа и синтеза СС.
Натурное моделирование - исследование на реальном объекте и обработке результатов экспериментов на основе теории подобия. Научный эксперимент, комплексные исследования, производственный эксперимент (исследуется широкая автоматизация, вмешательство в управление реальным процессом, создание критических ситуаций).
Физическое моделирование - на установках, которые сохраняют природу явлений при физическом подобии.
Кибернетическое моделирование - нет непосредственно физического подобия. Отображается S как "черный ящик" рядом входов и выходов.
Из всего вышесказанного и условий задания можно определить следующий вид модели:
v В зависимости изучаемых процессов: стохастическая – неизвестно сколько будет находиться деталей в накопителе при повторной обработке (известно, что если больше 3-х – активизируется второй станок); динамическое – необходимо узнать как система будет функционировать не в конкретный момент времени а на всем промежутки обработки 500-а деталей; непрерывное – из задания следует, что рассматривается автоматизированный конвейер.
v В зависимости от формы представления: вымышленное (абстрактное) – слишком дорого для студента материальное создание; к данной моделе применимы почти все варианты абстрактного моделирования (математическое, символьное т.д.) так, что нет смысла перечислять все.
Выбор математической схемы
Математическая схема - это участок при переходе от содержательного к формальному описанию процесса функционирования системы с учетом действия внешней среды.
То есть имеет место связка: "описательная модель - математическая схема - математическая (аналитическая и (или) имитационная) модель".
Каждая конкретная система S характеризуется набором свойств, то есть величин, отображающих поведение моделируемого объекта (реальной S) и учитывающих условия ее функционирования во взаимодействии с внешней средой (системой) Е.
При построении ММ системы решаются вопросы о полноте и упрощении. Полнота модели реализуется выбором границы " система S - среда Е ". Упрощение модели - выделение основных свойств S и отбрасывание второстепенных свойств (зависит от цели моделирования).
МАТЕМАТИЧЕСКИЕ СХЕМЫ ОБЩЕГО ВИДА
Модель S можно представить множеством величин, описывающих процесс функционирования реальной системы S.
Эти величины создают в общем случае четыре подмножества :
1) совокупность входных влияний на систему ![]() ;;
;;
2) совокупность влияний внешней среды![]() ;
;
3) совокупность внутренних параметров системы ![]()
4) совокупность выходных характеристик системы ![]() .
.
В этих подмножествах выделяются управляемые и неуправляемые переменные.
При моделировании S входные влияния, влияние внешней среды Е и внутренние параметры системы являются независимыми (экзогенными) переменными в векторной форме:
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() .
.
Выходные характеристики системы - зависимые (эндогенные) переменные.
![]() . (1)
. (1)
Процесс функционирования описывается оператором Fs, который пре-
образовывает экзогенные переменные в эндогенные :
![]() (2)
(2)
Совокупность зависимых выходных характеристик системы от времени (1) называется выходной траекторией ![]() (t), (2): называется законом функционирования системы S и обозначается Fs.
(t), (2): называется законом функционирования системы S и обозначается Fs.
В общем случае закон функционирования системы Fs может быть задан в виде функции, функционала, логических условий, алгоритма, таблицы, словесного правила соответствия.
Таким образом, математическая модель объекта (реальной системы) - это конечное подмножество переменных ![]() вместе с математическими связями между ними и характеристиками
вместе с математическими связями между ними и характеристиками ![]() .
.
ТИПОВЫЕ МАТЕМАТИЧЕСКИЕ СХЕМЫ
В практике моделирования объектов в области системотехники и системного анализа рациональней использовать типовые математические схемы:
v дифференциальные уравнения
v конечные автоматы
v вероятностные автоматы
v СМО (системы массового обслуживания).
ММ на основе этих схем:
1) детерминированные модели, когда при исследовании случайные факторы не учитываются, и системы функционируют в непрерывном времени, основанные на использовании дифференциальных, интегральных, интегро-дифференциальных и других уравнений.
2) детерминированные модели, которые функционируют в дискретном времени - конечные автоматы и конечно-разностные схемы.
3) стохастические модели (при учете случайных факторов) в дискретном времени - вероятностные автоматы.
4) стохастические модели в непрерывном времени - СМО.
Для больших информационно-управляющих систем (Ех, АСУ) типовые схемы недостаточны. Поэтому используют:
5) агрегативные модели (А-системы), которые описывают широкий круг объектов исследования с отображением системного характера этих объектов. При агрегативном описании сложная система разделяется на конечное число частей (подсистем), сохраняя при этом связи между взаимодействующими частями.
Итак, 5 подходов при построении ММ сложных систем :
1) непрерывно-детерминированный (D-схемы);
2) дискретно-детерминированный (R- схемы);
3) дискретно-стохастический (P- схемы);
4) непрерывно-стохастический (Q- схемы);
5) обобщенный или универсальный (А-схемы).
На основе сделанного выбора вида модели (непрерывно-стохастической) необходимо выбрать схему модели, исходя из определения схем (не вижу смысла описывать все схемы, а выбранная схема будет описана в следующей главе) для моей модели подходит Q-схема.
Аннотация
Данная курсовая работа должна показать уровень усвоения материала в области системного анализа и навыки при создании моделей систем.
Следует сразу заметить, что в этой курсовой работе не будет рассматриваться моделирование простых систем, т.к. их разработка довольно проста, а основные принципы одинаковы как для сложных систем, так и для простых. Так же не будут рассматривать начальные и основные понятия системного анализа, т.к. постановка задание подразумевает уклон на непосредственно моделирование системы, а не на разъяснения что такое система.
Похожие работы
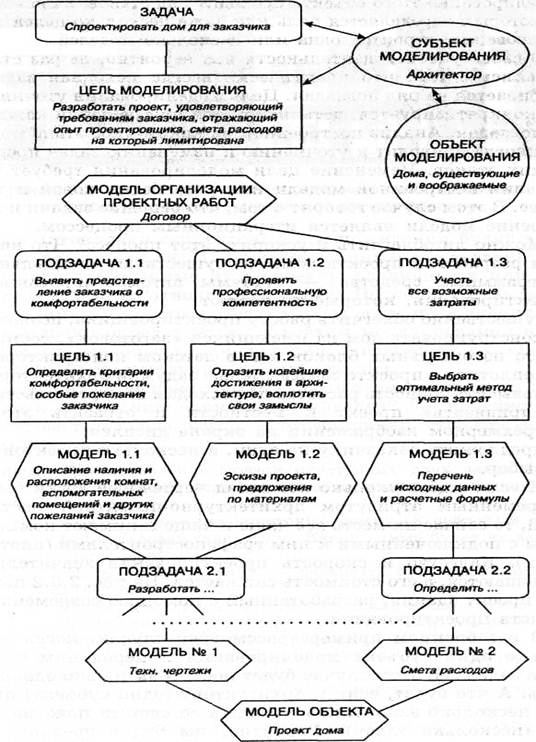
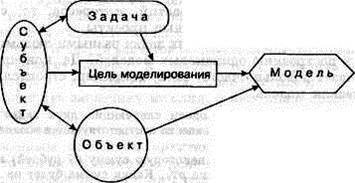
... вид информационного моделирования. Определим, кто в этом случае является субъектом моделирования, какая задача перед ним стоит, что может быть объектом и целью моделирования. Субъект моделирования — архитектор. Задача моделирования — спроектировать комфортабельный дом для семьи заказчика, расходы на проектирование и строительство которого не превысят заданной суммы. Объект моделирования — те ...
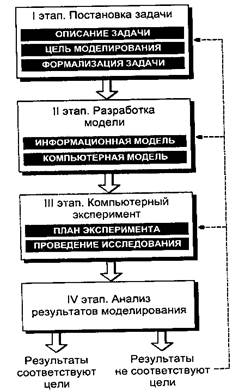
... и кропотливый процесс, требующий определённых знаний. В следующих параграфах вы познакомитесь с ним более подробно. Результатом этапа формализации и будет информационная модель. Но прежде, чем говорить об окончании процесса моделирования, построенную модель необходимо проверить на непротиворечивость и проанализировать, насколько она адекватна объекту и цели моделирования. Пример. Прочтите ...
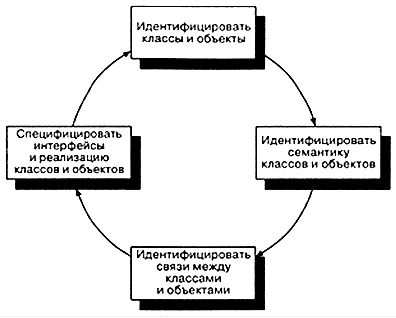
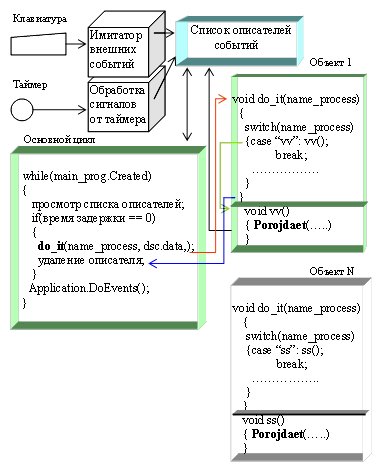
... ; case "vyx1_0": vyx1_0(main_prog); break; case "vyx0_1": vyx0_1(main_prog); break; } } 6. Организация процесса проектирования Г. Буч [12] выделяет в процессе проектирования программного приложения микро и макропроцессы. Микропроцесс объектно-ориентированной разработки приводится в движение потоком сценариев и архитектурных продуктов, которые порождаются и последовательно уточняются в ...
... Исследователи истории социологии считают, что если в XIX веке центром социологической мысли была Западная Европа, то начиная с 20-х годов XX в. США прочно удерживают позиции лидера в мировой социологии. Решающее влияние на бурное развитие социологии в США оказали два взаимосвязанных фактора: быстрое прохождение социологией всех пяти стадий внешней институционализации и большой объем конкретных, ...






0 комментариев