Заключительный оператор - слово вида stop(S), S - терм; вхождения переменных в терм S называются аргументами этого оператора;

2. заключительный оператор - слово вида stop(S), S - терм; вхождения переменных в терм S называются аргументами этого оператора;

3. оператор присваивания – F₀:=1; F₁:=1; F₂:=2; S:=4; F₀:=F₁; F₁:=F₂; F₂:=F₀+F₁; S:=S+F₂; S:=S–F₂;

4. условный оператор (тест) – логическое выражение; F₂<=M;

5. оператор петли - односимвольное слово While.

Графовая форма стандартной схемы на рис. 1.

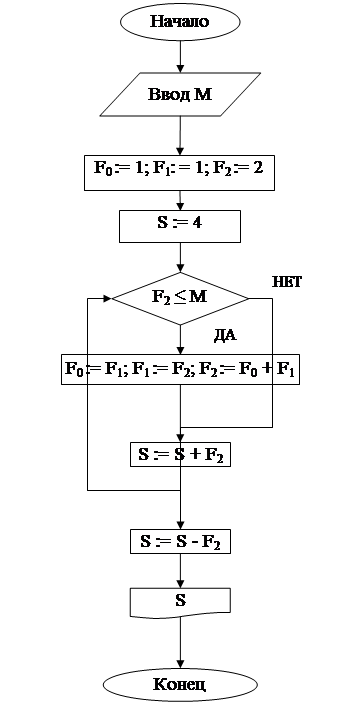
Рис. 1

 

Линейная форма стандартной схемы

Turbo Pascal

Program SummaFib;

Uses Crt;

Var M, {zadannoe chislo}

F0, F1, F2, {3 posledovatelnyh chisla Fibonachchi}

S : Integer; {summa chisel Fibonachi}

BEGIN

ClrScr;

Write('Vvedite naturalnoe M : ');

ReadLn(M);

F0:=1; F1:=1; F2:=2;

S:=4; {4 - summa pervih 3-h chisel Fibonachchi}

Write('Chisla Fibonachchi, ne prevoshodyaschie ', M, ' :', F0:4, F1:4);

While F2<=M do

begin

F0:=F1; F1:=F2; Write(F1 : 4);

F2:=F0+F1; S:=S+F2;

end;

S:=S-F2; {vychitanie iz summy poslednego chisla, kotoroe prevoshodit M}

WriteLn; WriteLn;

WriteLn('OTVET: Summa etih chisel ravna = ', S); ReadLn

END.

 

Задание 2

Построить базис рекурсивной схемы;

Составить интерпретацию для заданной рекурсивной схемы (рис. 2);

Составить протокол выполнения программы;

6

Составить рекурсивную программу-функцию подсчета количества всех положительных делителей натурального числа n.

Рассчитать количество делителей для числа 10.

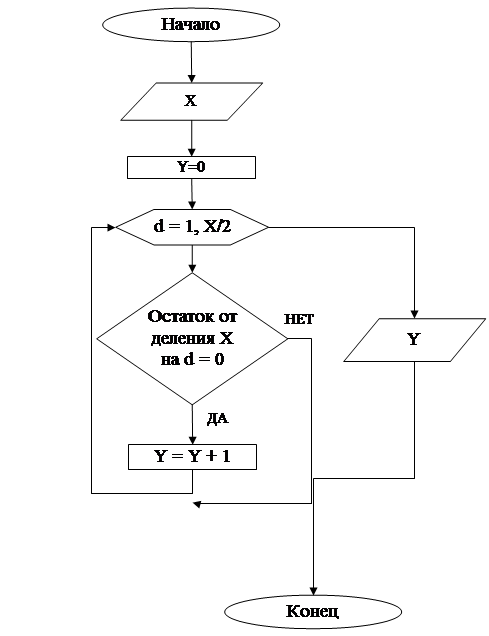
Рис. 2

 

TURBO PASCAL

program Chislo;

uses crt;

type r=array[1..10] of integer;

var

d,x:integer;

a:r;

y:integer;

begin

clrscr;

y:=1;

textcolor(6);

write('NAHOZHDENIE DELITELEJ');

gotoxy(2,2);

textcolor(9);

write('Vedite chislo, u kotorogo nado najti kolichestvo delitelej: ');

readln(x);

textcolor(6);

write ('Deliteli chisla ' ,x, ' : ');

for d:=1 to x div 2 do

begin

textcolor(9);

if x mod d=0 then begin

write(d,' ');

inc(y);end;end; {Y:= Y + 1}

writeln(x);

textcolor(5);

write('Kolichestvo delitelej: ' ,y);

readln;

end.

Результат работы PASCAL-программы (рис. 3)

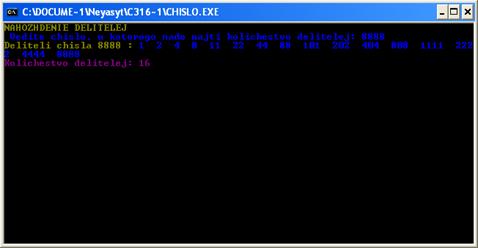
Рис. 3

 

Задание 3

Разработать алгоритм программы, решающей поставленную задачу;

Составить стандартную схему программы и записать полученную программу в линейной форме (рис. 4);

Для каждого оператора программы, записанного в линейной форме определить слабейшие предусловия.

6	Расчет суммы чисел Фибоначчи

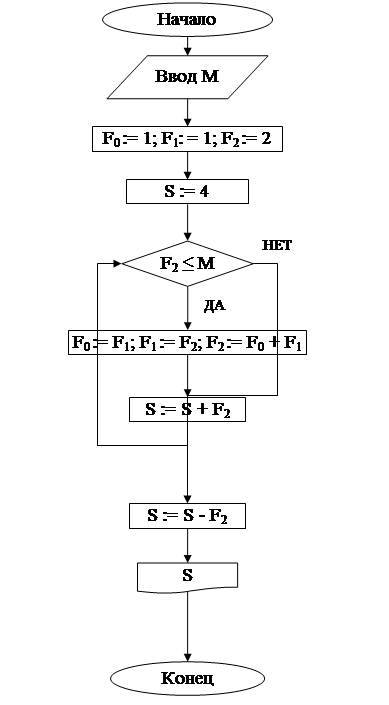
Рис. 4

Turbo Pascal

Program SummaFib;

Uses Crt;

Var M, {Zadannoe chislo}

F0, F1, F2, {3 posledovatelnyh chisla Fibonachchi}

S : Integer; {Summa chisel Fibonachch}

BEGIN

ClrScr;

Write('Vvedite naturelnoe chislo M: ');

ReadLn(M);

F0:=1; F1:=1; F2:=2;

S:=4; {4 - summa pervyh 3-x chisel Fibonachchi}

Write('Chisla Fibonachchi, ne prevoshodyaschie ', M, ' :', F0:4, F1:4);

While F2<=M do

begin

F0:=F1; F1:=F2; Write(F1 : 4);

F2:=F0+F1; S:=S+F2;

end;

S:=S-F2; {vychitanie iz summy poslednego chisla, kotoroe prevoshodit M}

WriteLn; WriteLn;

WriteLn('O T V E T: Summa etih chisel ravna ', S); ReadLn

END.

Результаты работы Pascal-программы (рис. 5).

Рис. 5

Слабейшие предусловия операторов:

1. начальный оператор - слово вида start (F₀, F₁, F₂), где F₀ = 1, F₁ = 1,

F₂ - переменные, называемые результатом этого оператора;