Навигация
Выбор параметров обучения
2.3 Выбор параметров обучения
Находим оптимальные параметры:
• скорость обучения в интервале от 0 до1
• момент в интервале от 0 до 1
• начальные веса от 0 до 1
1. Зависимость качества обучения от скорости обучения
| Скорость обучения | 0,1 | 0,5 | 0,7 | 1 |
| Мин. ср. ошибка на тест. наборе | 0,0019529 | 0,0006956 | 0,0005016 | 0,0002641 |
2.Зависимость качества обучения от момента
| Момент | 0,1 | 0,5 | 0,7 | 1 |
| Мин. ср. ошибка на тест. наборе | 0,0019529 | 0,0012411 | 0,0013824 | 0,5690943 |
3.Зависимость качества обучения от начальных весов
| Начальный вес | 0,1 | 0,3 | 0,7 | 1 |
| Мин. ср. ошибка на тест. наборе | 0,0010359 | 0,0019529 | 0,0032182 | 0,0031102 |
2.4 Оптимальные параметры обучения
Скорость обучения: 0,1
Начальный момент: 0,1
Начальные веса: 0,3
Модель - Сеть Ворда с двумя блоками в скрытом слое.
Структура НС:
1. количество слоев: 4
2. количество нейронов:
1) блок 1: 63
2) блок 2: 24
3) блок 3: 24
4) блок 4: 9
3. вид функций активации:
1) блок 1 – линейная [0;1]
2) блок 2 –гауссова
3) блок 3 –гауссова
4) блок 5 – логистическая.
2.5 Блок-схема алгоритма обучения
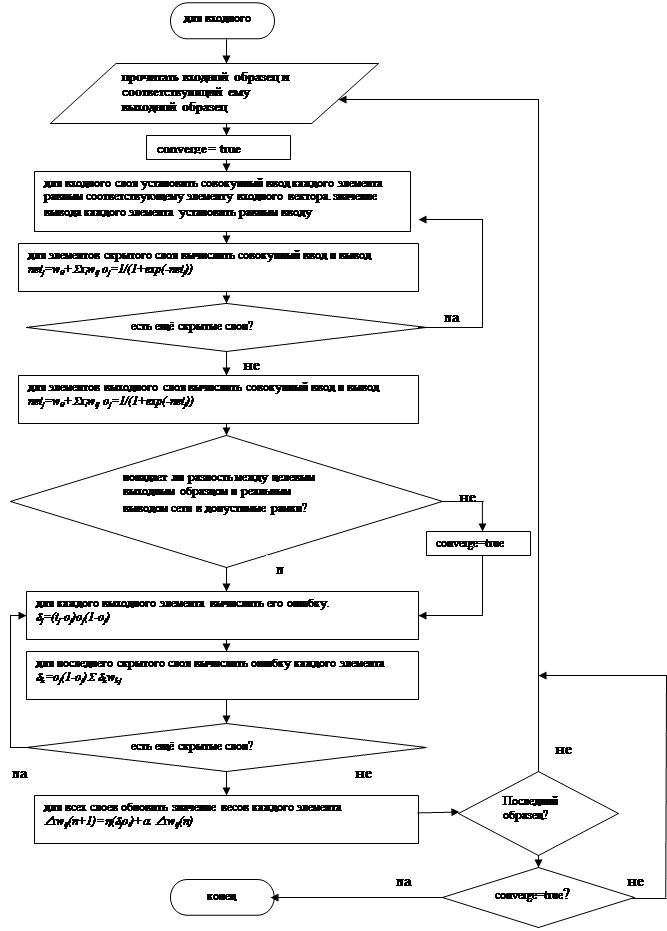
3. Анализ качества обучения
При данных оптимальных параметрах результаты применения сети можно представить виде таблицы
| Вых1 | Вых2 | Вых3 | Вых4 | Вых5 | Вых6 | Вых7 | Вых8 | Вых9 | |
| R квадрат | 1.0000 | 0.9992 | 0.9999 | 1.0000 | 0.9999 | 1.0000 | 0.9995 | 1.0000 | 1.0000 |
| СКО | 0.002 | 0.009 | 0.003 | 0.001 | 0.003 | 0.001 | 0.021 | 0.001 | 0.002 |
| Относ СКО % | 0.152 | 0.910 | 0.275 | 0.107 | 0.320 | 0.133 | 2.112 | 0.128 | 0.153 |
| доля с ош <5% | 10.417 | 12.500 | 13.194 | 9.722 | 9.722 | 11.111 | 10.417 | 9.722 | 12.500 |
| доля с ош 5-10% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| доля с ош 10-20% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| доля с ош 20-30% | 0 | 0 | 0 | 0 | 0 | 0 | 0.694 | 0 | 0 |
| доля с ош >30% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Для проверки способностей к обобщению на вход сети подаются зашумленные последовательности входных сигналов. Процент зашумления показывает, какое количество битов входного вектора было инвертировано по отношению к размерности входного вектора.
Для зашумления 5% сеть выдает такие результаты:
| Вых1 | Вых2 | Вых3 | Вых4 | Вых5 | Вых6 | Вых7 | Вых8 | Вых9 | |
| Rквадрат | 0,9868 | 0,9884 | 0,9800 | 0,9831 | 0,9843 | 0,9830 | 0,9814 | 0,9855 | 0,9838 |
| СКО | 0,036 | 0,034 | 0,044 | 0,041 | 0,039 | 0,041 | 0,043 | 0,038 | 0,040 |
| Относ СКО % | 3,616 | 3,385 | 4,448 | 4,089 | 3,942 | 4,096 | 4,289 | 3,781 | 3,998 |
| доля с ош<5% | 11,111 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| доля с ош5-10% | 0 | 11,111 | 11,111 | 0 | 0 | 11,111 | 0 | 11,111 | 11,111 |
| доля с ош 10-20% | 0 | 0 | 0 | 11,111 | 11,111 | 0 | 11,111 | 0 | 0 |
| доля с ош 20-30% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| доля с ош>30% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Далее мы подавали различное количество инвертированных битов.
В таблице представлена зависимость количества инвертированных битов от количества правильных ответов на выходе
| Количество инвертированных битов | Количество верных ответов на выходе |
| 50 | 0 |
| 25 | 2 |
| 13 | 9 |
| 19 | 6 |
| 16 | 7 |
| 15 | 8 |
| 14 | 8 |
Таким образом мы выявили критическое количество зашумленных данных = 16 на каждый входной вектор.
Это соответствует 20% зашумления. При большем зашумлении входных данных сеть не может отдать предпочтение одной цифре, причем с увеличением зашумления количество таких букв растет.
Результаты сети при критическом зашумлении:
| Вых1 | Вых2 | Вых3 | Вых4 | Вых5 | Вых6 | Вых7 | Вых8 | Вых9 | |
| R квадрат | 0,7193 | 0,8274 | 0,6583 | 0,7303 | 0,7928 | 0,6981 | 0,9135 | 0,8702 | 0,7746 |
| СКО | 0,028 | 0,017 | 0,034 | 0,027 | 0,020 | 0,030 | 0,009 | 0,013 | 0,022 |
| Относ СКО % | 16,650 | 13,057 | 18,369 | 16,322 | 14,304 | 17,268 | 9,243 | 11,321 | 14,922 |
| доля с ош <5% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| доля с ош 5-10% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| доля с ош 10-20% | 0 | 11,111 | 0 | 0 | 11,111 | 0 | 0 | 0 | 0 |
| доля с ош 20-30% | 0 | 0 | 0 | 0 | 0 | 0 | 11,111 | 0 | 11,111 |
| доля с ош >30% | 11,111 | 0 | 11,111 | 11,111 | 0 | 11,111 | 0 | 11,111 | 0 |
Судя по анализу качества обучения, сеть хорошо справляется при 20% зашумлении.
Это говорит о том что у сети неплохой потенциал для обобщения.
Выводы
В ходе данной курсовой работы были получены навыки моделирования нейронных сетей, а также была решена частная задача моделирования нейронной сети для классификации римских цифр. Исходными данными для сети являлись изображения римских цифр, представленные виде матриц, размерностью 7х9.
Обученная нейронная сеть хорошо себя показала при 20% уровне шума. Для увеличения этого показателя нужно снизить риск возникновения критических шумов. Этого можно достигнуть путем увеличения размерности сетки.
Список использованных источников
1 Стандарт предприятия СТП 1–У–НГТУ–98
2 Круглов В.В., Борисов В.В. Искусственные нейронные сети. Теория и практика. – М.: Горячая линия – Телеком, 2001. – 382 с.:ил.
3 Электронный учебник по NeuroShell 2
4 Каллан Р. Основные концепции нейронных сетей
5 Ресурсы сети Интернет
Похожие работы
... производительных сил, тем быстрее повышается Б. населения. В еще большей степени Б. связано с эффективностью социально-экономической политики в данном обществе. Информатика как наука. Предмет и объект прикладной информатики. Системы счисления Инфоpматика — это основанная на использовании компьютерной техники дисциплина, изучающая структуру и общие свойства информации, а также закономерности и ...
... мозгу (1), где через вставочный нейрон передаются на эфферентные волокна (эфф. нерв), по которым доходят до эффектора. Пунктирные линии - распространение возбуждения от низших отделов центральной нервной системы на ее вышерасположенные отделы (2, 3,4) до коры мозга (5) включительно. Наступающее вследствие этого изменение состояния высших отделов мозга в свою очередь воздействует (см. стрелки) на ...
... также, сколь прямолинейно философы подходят к биологическим проблемам. В связи с этим мне особенно нравится употребление Декартом слова "просто" если бы так оно и было... Как следует понимать эти картезианские метафоры памяти? Возможно, Декарт считал свою теорию таким же точным описанием процессов, происходящих в мозгу, каким для Гарвея было сравнение сердца с насосом. Но мне кажется, что мы ...
... и аппаратной реализации, выполненные на этом языке описания, переводятся на более подходящие языки другого уровня. 4. Экспертные системы (ЭС), их структура и классификация. Инструментальные средства построения ЭС. Технология разработки ЭС 4.1 Назначение экспертных систем В начале восьмидесятых годов в исследованиях по искусственному интеллекту сформировалось самостоятельное направление ...


0 комментариев