Электрическое поле падающей волны направлено по оси z

1. Электрическое поле падающей волны направлено по оси z.

Поместим на пути рассеянного света поляризационную призму и повернем ее так, чтобы в одном случае вектор поляризации  был направлен по оси х, а во втором случае – по оси z. Обозначим соответствующие интенсивности рассеянных лучей через  и . Для х – компоненты рассеянного луча  и из (1) получаем:

 (3)

Для z – компоненты  и

(4)

Полная интенсивность равна сумме интенсивностей:

 (5)

2. Электрическое поле падающей волны направлено по оси у.

Ориентируем поляризационную призму так, чтобы сначала вектор поляризации  был направлен по оси х, а потом по оси z. В обоих случаях  и поэтому

(6)

и полная интенсивность

 (7)

3. Коэффициент деполяризации.

В случае, когда падающий луч поляризован так, что его электрический вектор направлен по оси z, а наблюдение рассеянного луча происходит по оси у, коэффициент деполяризации обозначают через :

(8)

В другом случае, когда электрический вектор в падающем луче направлен по оси у (горизонтально), совпадающим с направлением наблюдения рассеянного луча, коэффициент деполяризации обозначается  и согласно формуле (6)

(8 ^/ )

Наконец, когда падающий луч неполяризован, то из формул:

 

(9)

получим

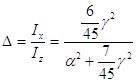 (10)

Если молекулы изотропны, то  и .

Связь между коэффициентами деполяризации  и  следующая:

(11)

Измерение коэффициента деполяризации  или  позволяет рассчитать оптическую анизотропию молекул :

.

Экспериментальное определение коэффициента деполяризации

Экспериментально определение коэффициента деполяризации света, рассеянного МЖ производилось с помощью фотоэлектрического метода. Источником света служил гелий-неоновый лазер  мощностью 2 мВт, установленный так, чтобы колебания светового вектора происходили в плоскости XOZ, как указано на рис. 2, вектор  параллелен оси z. Интенсивность рассеянного света регистрировалась с помощью ФЭУ-27 под углом 90⁰ к направлению распространения света (по оси у на рис. 2). Компоненты интенсивности рассеянного света  и  поляризованные соответственно параллельно осям z и х выделялись с помощью призмы Аренса, а коэффициент деполяризации определялся как отношение этих компонентов в соответствии с формулой (8):

Во втором случае лазер устанавливался так, чтобы колебания вектора  излучения лазера происходили в плоскости YOZ, и вектор  был направлен по оси у. Призма Аренса ориентировалась так, чтобы выделить компоненту  (вектор поляризации  направлен по оси х) и  (вектор  направлен по оси z). Коэффициент деполяризации определялся как отношение этих компонентов по формуле (8 ^/ )

 

В третьем случае падающий луч был неполяризован (свет от лампы КГМ) т определялись две компоненты  и  соответствующей ориентировкой призмы Аренса, а коэффициент деполяризации определялся по формуле (10):

Для уменьшения погрешности измерения свет модулировался прерывателем и регистрировался ФЭУ-27, сигнал с которого подавался на вход осциллографа С8-13.

Исследованные МЖ представляли собой коллоидные растворы магнетита и феррита кобальта в керосине. Объемные концентрации исследованных образцов составляли:

Проведенные измерения показали, что значения коэффициентов деполяризации  и  составили:

Относительная ошибка измерений коэффициентов деполяризации составляет:

 

Расчет коэффициента деполяризации

Расчет коэффициента деполяризации для частиц магнетита со средним размером частиц 10 нм, апрокисмируемых эллипсоидами вращения с отношением осей , диэлектрической проницаемости магнетита на оптической частоте  и диэлектрической проницаемостью керосина , по формуле классической теории деполяризации для газов:

  

выполнил Ю.Н. Скибин, который при заданных параметрах получил значение . Сравнив это значение с экспериментально наблюдаемым , Скибин пришел к выводу, что деполяризацию света, рассеянного МЖ на основе магнетита в керосине при объемной концентрации порядка – 0,1 % невозможно объяснить только анизотропией поляризуемости коллоидных частиц, и предложил учесть диполь-дипольное взаимодействие частиц, которое приводит к взаимной корреляции магнитных моментов, а следовательно и осей несферических коллоидных частиц. С этой целью вводится  - средняя анизотропия тензора поляризуемости и коэффициент , учитывающий взаимодействие частиц, а формула для коэффициента деполяризации принимает вид:

где для идеального газа , а для взаимодействующих частиц .

Воспользовавшись теорией Орнштейна – Цернике [Ансельм А.И. Теория электрооптических явлений в неполярных жидкостях //ЖЭТФ. – 1947. – Т. 17, вып. 6 – С. 489-506], ему удалось получить для однодоменных частиц магнетита со средним размером 11 нм при объемной концентрации частиц 0,1 % и температуре 300 К значение коэффициента .

Согласно нашим оценкам, если рассматривать эллипсоид вращения, состоящий из двух объединившихся частиц, размер которых порядка 10 нм, соотношение осей  то , что в 23 раза превосходит результат, полученный Скибиным Ю.Н. при соотношении осей .

Понятно, что это оценки лишь по порядку величины, но если учесть, что в жидкости существуют агрегаты не только из двух частиц, но из 3, 4 и т.д., то результаты по рассеянию света могут быть объяснены в модели цепочечных агрегатов частиц.

Зависимость коэффициента деполяризации от концентрации.

 

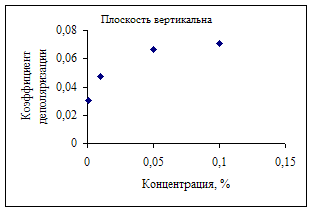
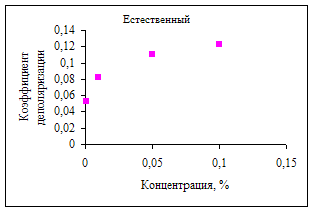
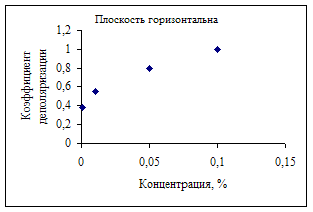
Одним из возможных путей изучения механизма светорассеяния является исследование динамики рассеяния света в импульсных электрических и магнитных полях.

Схема экспериментальной установки, предназначенной для изучения процессов рассеяния света магнитной жидкостью в импульсных магнитных полях, представлена на рисунке 4.

3 2

С8 – 13

УПТ

4 5

Н

Б5-24А

1 Р 7

Р^/ 6

С1 – 65 А

11

8

ГПИ

 

R_доб

12

ЛИПС

9

10

Рис.4 Экспериментальная установка для изучения рассеяния света в импульсных магнитных полях.

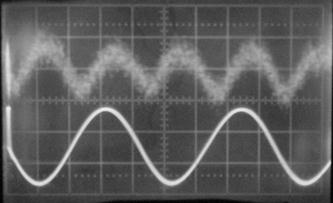
Она представляет собой кювету цилиндрической формы 3, изготовленную из стекла и расположенную в области однородного магнитного поля катушек Гельмгольца 2, создающих магнитное поле напряженностью до 8 кА/м. Источником света служит гелий-неоновый лазер 1 с длиной волны 632,8 нм. Для создания импульсов магнитного поля используется генератор напряжения прямоугольной формы 8, управляющий работой транзисторного ключа. На базу транзистора 9 подается управляющий импульс напряжения прямоугольной формы амплитудой порядка 9 В. Форма импульса магнитного поля контролируется по форме тока, протекающего в катушках, при помощи электронного осциллографа С – 65 А (11), включенного параллельно добавочному сопротивлению 12, величиной 1 Ом.

Регистрация рассеянного света производилась при помощи фотоэлектронного умножителя ФЭУ – 27 при различных углах наблюдения . Сигнал с ФЭУ усиливался с помощью усилителя постоянного тока 5 и подавался на вход запоминающего осциллографа 6. Плоскость поляризации падающего света РР^/ была установлена перпендикулярно плоскости наблюдения.

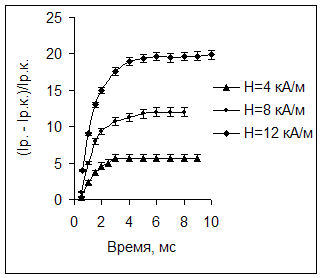
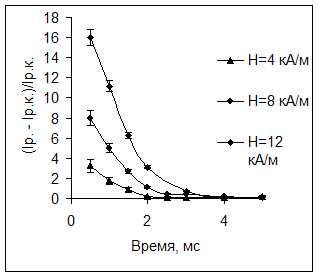
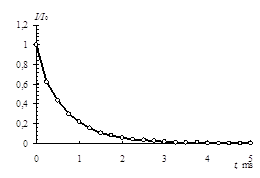
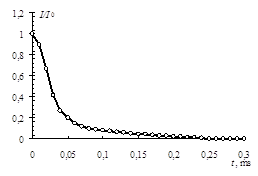
По полученным данным были построены кривые нарастания интенсивности и кривые уменьшения интенсивности рассеянного света со временем, после выключения магнитного поля. Используя эти кривые можно рассчитать коэффициент вращательной диффузии , а затем найти гидродинамический диаметр частицы из соотношений:

, , , ,

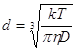где Дж/К, , .

Подставляя полученные данные в конечную формулу, находим, что .

Таким образом, можно сделать вывод, что рассеяние света МЖ в магнитном поле определяется агрегатами, состоящими из нескольких десятков частиц.

ЦИТИРУЕМАЯ ЛИТЕРАТУРА

1.      Аксельрод Л.А., Гордеев Г.П., Драбкин Г.М., Лазебник И.М., Лебедев В.Г. Анализ малоуглового рассеяния поляризованных нейтронов в ненамагниченных феррожидкостях // ЖЭТФ. – 1986. – Т. 91, вып. 2(8). – С. 531-541.

2.       Берковский Б.М., Медведев В.Ф., Крипов Н.С. Магнитные жидкости. – М.: Химия, 1989. – 240 с.

3.       Бибик Е.Е. Приготовление феррожидкостей // Коллоидный журнал. – 1973. – Т.35, №6. – с. 1141.

4.       Бибик Е.Е. Эффекты взаимодействия частиц в дисперсных ферромагнетиках: Автореф. дис. … докт. хим. наук. Л.: ЛТИ, 1971.

5.       Бибик Е.Е. Магнитооптический эффект агрегирования в поперечном электрическом поле // Коллоид. Журнал. – 1970. – Т. 32. №2. – с. 307.

6.       Бибик Е.Е., Бузунов О.В. Достижения в области получения и применения ферромагнитных жидкостей /ЦНИИ «Электроник». – М., 1979. – 60 с.

7.       Блум Э.Я., Майоров М.М., Цеберс А.О. Магнитные жидкости. – Рига: Зинатне, 1986. – 386 с.

8.       Борен К., Хафмен Д. Поглощение и рассеяние света малыми частицами: Пер с англ. – М.: Мир, 1986. – 664 с.

9.       Воюцкий С.С. Курс коллоидной химии. – М.: Химия, 1976. – 512 с.

10.    Вукс М.Ф. Рассеяние света в газах, жидкостях и твердых растворах. Л.: ЛГУ, 1977, 320 с.

11.    Гермашев В.Г. Стабилизация углеводородных феррожидкостей поверхностно-активными веществами. Дис. … канд. физ.-мат. наук. – Л., 1976. – 135 с.

12.    Диканский Ю.И. Эффекты взаимодействия частиц и структурно-кинетические процессы в магнитных коллоидах: Автореф. … докт. физ.-мат. наук. – Ставрополь, 1999, 35 с.

13.    Дроздова В.И., Скибин Ю.Н., Шагрова Г.В. Исследование структуры разбавленных магнитных жидкостей по анизотропному рассеянию. Магнитная гидродинамика, 1987, №2, С. 63-66.

14.    Елфимова Е.А. Эффективная магнитная проницаемость агрегированной феррожидкости: влияние фрактальных агрегатов // Сб. научных Трудов 10 международной конференции по магнитным жидкостям 2002. C.142-147.

15.    Зубарев А.Ю. К теории кинетических явлений в умеренно концентрированных магнитных жидкостях //Коллоидный журнал. – 1995. – Т. 57, №3. – С. 335 – 341.

16.    Зубарев А.Ю. Юшков А.В., Искакова Л.Ю. К теории динамических свойств неразбавленных магнитных жидкостей. Эффект цепочечных агрегатов // Магнитная гидродинамика. – 1998. – Т.34. №4. – С. 324 – 335.

17.    Зубарев А.Ю., Исканова Л.Ю., Романчук А.П. Фазовые переходы в магнитореологических суспензиях // Сб. науч. Трудов 10 международной конференции по магнитным жидкостям 2002. – C. 124-128

18.    Ландсберг Г.С. Оптика. М.: Наука, 1976.- 928 с.

19.    Магнитные жидкости в машиностроении /Д.В. Орлов и др.: Под общей ред. Д.В. Орлова, В.В. Подгорнова. – М.: Машиностроение. 1993. - 272 с.

20.    Надворецкиий В.В., Соколов В.В. Поглощение ультразвука в магнитной жидкости с эллипсоидальными агрегатами // Магнитная гидродинамика. – 1997. – Т. 33, №1. – С. 30-34.

21.    Падалка В.В., Ерин К.В. Оптический метод обнаружения агрегатов в разбавленных магнитных коллоидах // Сборник научных трудов 10-й Международной Плесской конференции по магнитным жидкостям. Иваново: Изд-во ИГЭУ, 2002. – С. 162 – 167.

22.    Пшеничников А.Ф., Шурубер И.Ю. Расслоение магнитных жидкостей: условия образования и магнитные свойства капельных агрегатов // Известия АН СССР сер. физ.- 1987. – Е. 51б №6. – С. 1081-1087.

23.    Розенцвейг Р. Феррогидродинамика. – М.: Мир. 1989. – 357 с.

24.    Скибин Ю.Н. Молекулряно-кинетический механизм электро- и магнитооптических явлений в магнитных жидкостях. Дис. … доктора физ.-мат. наук. – Ставрополь, 1996. – 319 с.

25.    Скибин Ю.Н. Деполяризация света рассеянного магнитной жидкостью // Коллоид. Ж. – 1984. – Т. 46, №5. – С. 955-960.

26.    Такетоми С., Тикадзуми С. Магнитные жидкости. – М.: Мир, 1993. – 272 с.

27.    Фабелинский И.Л. Молекулярное рассеяние света. М.: Наука, 1965. – 512 с.

28.    Фетрман В.Е. Магнитные жидкости. – Минск: Вышейшая школа., 1988. – 184 с.

29.    Физическая энциклопедия / Гл. ред. А.М. Прохоров. – М.: Сов. энциклопедия. – Т.2. 1990. – С. 673 – 675.

30.    Фролов Ю.Г. Курс коллоидной химии. – М.: Химия, 1982. – 400 с.

31.    Цеберс А.О. Образование и свойства крупных конгломератов магнитных частиц // Магнитная гидродинамика. – 1983. - №3. – С. 3 – 11.

32.    Цеберс А.О. Термодинамическая устойчивость магнитных жидкостей // Магнитная гидродинамика. – 1982. - №2. – C. 42 – 48.

33.    Цеберс А.О. К вопросу о причинах образования микрокапельных агрегатов в коллоидных системах ферромагнетиков // Магнитная гидродинамика. – 1987 . - № 3. – C. 143-145.

34.    Чеканов В.В. Возникновение агрегатов как фазовый переход в магнитных коллоидах /В кн.: физические свойства магнитных жидкостей. – Свердловск. – 1983. – C. 42 – 49.

35.    Шлиомис М.И. Магнитные жидкости //Успехи физических наук. – 1974. – Т. 112. – С. 427 – 458.

36.    Эскин В.Е. Рассеяние света растворами полимеров и свойства макромолекул. – Л.: Наука, 1986, 288 с.

37.    Bean C.P., Livingston I.D. Superparamagnetism // J. Appl. Phys. – 1959. – V. 30S №4. – P. 120S – 129S.

38.    Berkowitz, Zahut J.A., Van Buren C.E. Properties of magnetic fluid particles. //Transactions of Magnetic – 1980. V. 16. №2. – P. 184 – 190.

39.    Brown W.E. Magnetic interactions of superparamagnetic particles // J. Appl. Phys. – 1967. – V. 38, №3. – P. 1017 – 1018.

40.    Brown W.F. Themal fluctuations of a single-domain particle //Phys. Rex. – 1963. – V. 130. №5. – P. 1677 – 1686.

41.    Chikazumi S., Taketomi S., Ukita M., Mizukami M., Miyajima Н., Setogawa M., Kurihara Y. Physics of magnetic fluids // Journal of Magnetism and Magnetic Materials. – 1987. – V. 65. – P. 245-251.

42.    Hayes C.K. Observation of association a ferromagnetic colloid // Journal of Colloid and Interface Science. – 1975. – V. 52, №2. – P. 239-243.

43.    Jordan P.C. Field dependent chain formation by ferromagnetic colloids // Molecular Physics. – 1979. – V. 38. №3. – p. 769 – 780.

44.    Martinet Т.A. Birefrigence at dichroisme lineaire des ferrofluids sous champ magnetique // Rheologiec Acta. – 1974. – V. 52. №3. – P. 260 – 264.

45.    R.V. Mehta Scattering and polarization of light by magnetic fluids // IEEE. Transaction on Magnetic. – 1980. – V. – MAG-16. №2. – P. 203-206.

46.    Neel Z. Influence des fluctuations thermiques sur l’aimantation de grains ferromagnetiques tres fins. //Acad des sciences. Complet rendu. – 1949. – V. 228, №8, - Р. 664 – 666.

47.    Neel Z. Theoric du triage magnetique ferromagnetiques on grains fins avec application soux terres cuites // Ann. Geophys. – 1949. V. 5. №2. – P. 99 – 120.

48.    Neitzel U.,Barner K. Optical measurement on ferromagnetic colloids // Physics letters. – 1977. – V.63, №3. – P.327-329.

49.    Sano K., Doi M. Theory of agglomeration of ferromagnetic particles in magnetic fluids //J. Phys. Soc. Jap. – 1983. – V. 52. №8. – P. 2810 – 2815

50.    Scholten P.C. The origin of magnetic birefringence and dichroism in magnetic fluids // IEEE Translations Magnetics Vol Mag-16, 1980, №2, P. 221-225.

51.    Taketomi S., Takahashi H., Inaba N., Miyajim H. Experimental and Theoretical Investigations on Agglomeration of Magnetic Colloid Particles in Magnetic fluids // Journal of the Physical Particles in Magnetic fluids // Journal of the Physical Society of Japan. – 1991. V. 60, №5. – P. 1689-1707.

52.    Wayen Reed, Janson H. Fendler. Anisotropic aggregates as the origin of magnetically induced dichroism in ferrofluids // J. Appl. Phys. 59(8), 15 April 1986, P. 2914 – 2924.