Навигация
Содержание и объем понятия
1.2 Содержание и объем понятия
Всякое понятие имеет содержание и объем. Содержанием понятия называется совокупность существенных признаков одноэлементного класса или класса однородных предметов, отраженных в этом понятии. Содержанием понятия "квадрат" является совокупность двух существенных признаков: "быть прямоугольником" и "иметь равные стороны",
Объемом понятия называют совокупность (класс) предметов, которая мыслится в понятии. Объективно, т.е. вне сознания человека, существуют различные предметы, например, школьники. Под объемом понятия "школьник" подразумевается множество всех школьников, которые существуют сейчас, существовали ранее и будут существовать в будущем. Класс (или множество) состоит из отдельных объектов, которые называются его элементами. В зависимости от их числа множества делятся на конечные и бесконечные. Например, множество столиц государств конечно, а множество натуральных чисел бесконечно. Множество (класс) А называется подмножеством (подклассом) множества (класса) В, если каждый элемент А является элементом В. Такое отношение между подмножеством А и множеством В называется отношением включения класса А в класс В и записывается так: А с В. Читается: класс А входит в класс В. Это отношение вида и рода (например, класс "стол" входит в класс "мебель").
Отношение принадлежности члемента а классу А записывается так: а Є А. Читается: элемент а принадлежит классу А. Например, а — "нева" и А - "река". Классы А и В являются тождественными (совпадающими), если А с В и В с А, что записывается как А= В.
Закон обратного отношения между объемами и содержаниями понятий
В этом законе речь идет о понятиях, находящихся в родовидовых отношениях. Объем одного понятия может входить в объем другого понятия и составлять при этом лишь его часть. Например, объем понятия "хищная рыба" целиком входит в объем другого, более широкого по объему понятия "рыба" (составляет часть объема понятия "рыба"). При этом содержание первого понятия оказывается шире, богаче (содержит больше признаков), чем содержание второго. На основе обобщения такого рода примеров можно сформулировать следующий закон: чем шире объем понятии, тем уже его содержание, и наоборот. Этот закон называется законом обратного отношения между объемами и содержаниями понятии. Он указывает на то, что чем меньше информации о предметах, заключенной в понятии, тем шире класс предметов и неопределеннее его состав (например, "водопад"), и, наоборот, чем больше информации в понятии (например, "крупный водопад" или "крупный водопад в Канаде"), тем уже и определеннее круг его предметов, или даже мыслится только один предмет.
2. Отношения между понятиями
Предметы мира находятся друг с другом во взаимосвязи и взаимообусловленности. Поэтому и понятия, отражающие эти предметы, также находятся в определенных отношениях. Далекие друг от друга по своему содержанию понятия, не имеющие общих признаков, называются несравнимыми (например, "поэма" и "колодец"; "невоспитанность" и "радуга"), остальные понятия называются сравнимыми.
Сравнимые понятия делятся по объему на совместимые (объемы этих понятий совпадают полностью или частично) и несовместимые (их объемы не имеют общих элементов).
В отношении противоположности (контрарности) находятся объемы таких двух понятий, которые являются видами одного и того же рода, и притом одно из них содержит какие-то признаки, а другое эти признаки не только отрицает, но и заменяет их другими, исключающими (т.е. противоположными признаками). Слова, выражающие противоположные понятия, являются антонимами. Антонимы широко используются в обучении. Примеры противоположных понятий: "великан" — "карлик"; "белые туфли" -"черные туфли". Объемы последних двух понятий разделены объемом некоторого третьего понятия, куда, например, входит понятие "коричневые туфли".
В отношении противоречия (контрадикторности) находятся такие два понятия, которые являются видами одного и того же рода, и при этом одно понятие указывает на некоторые признаки, а другое эти признаки отрицает. Исключает, не заменяя их никакими другими признаками. Если одно понятие обозначить А (например, "глубокое озеро"), то другое понятие, находящееся с ним в отношении противоречия, следует обозначить не-А (т.е. "неглубокое озеро"). Круг Эйлера, выражающий объем таких понятий, делится на две части (А и не-А), и между ними не существует третьего понятия. Например, товар может быть либо дорогой, либо недорогой; комната бывает светлой или несветлой; животное - позвоночным или беспозвоночным и т.д. Понятие А является положительным, а понятие не-А — отрицательным. Понятия А и не-А также являются антонимами.
3. Определение понятий
Определение (дефиниция) (от лат. (definitio — определение) понятия — логическая операция раскрытия содержания понятия или значения термина.
С помощью определения понятий мы в явной форме раскрываем содержание понятия и тем самым отличаем круг определяемых предметов от других предметов.
Примеры: "Информатика — наука, предметом которой являются процессы и системы получения, хранения, передачи, распространения, использования и преобразования информации" (1); "Правильной дробью называется простая дробь, числитель которой меньше знаменателя" (2).
Давая такие определения, мы отличаем науку информатику от других наук, а правильные дроби от всех других дробей, например неправильных или десятичных.
Приведем еше несколько определений понятий, взятых из школьных учебников, которые принадлежат к двум различным видам определений (реальным и номинальным). "Зоология — это наука о животных, об их разнообразии, строении, поведении, размножении, развитии, происхождении, а также о значении в природе и жизни человека" (3); "Слово зоология происходит от двух греческих слов: эоон — животное и логос — слово, учение, наука" (4). "Число, которое показывает, во сколько раз уменьшены (увеличены) настоящие расстояния на чертеже, называется масштабом" (5).
Понятие, содержание которого надо раскрыть, называется определяемым понятием (definiendит, сокращенно Dfd), а то понятие, посредством которого оно определяется, называется определяющим понятием (definience, сокращенно Dfn). Правильное определение устанавливает между ними отношение равенства (эквивалентности).
Определения делятся на явные и неявные. В явных определениях даны определяемое понятие и определяющее, объемы которых равны, т.е. Dfd= Dfn. К их числу относится самый распространенный способ определения через ближайший род и видовое отличие, где формулируются существенные признаки определяемого понятия. Например: "Барометр — прибор для измерения атмосферного давления"; "Треугольник — многоугольник с тремя сторонами"; "Гротеск — способ сатирического изображения жизни, отличающийся резким преувеличением, сочетанием реального и фантастического".
Признак, указывающий на тот крут предметов, из числа которых нужно выделить определяемое множество предметов, называется родовым признаком, или родом. В приведенных выше примерах это "прибор", "многоугольник", "способ сатирического изображения жизни". Признаки, при помощи которых выделяется определяемое множество предметов из числа предметов, соответствующих родовому понятию, называются видовым отличием (их может быть один или несколько).
Разновидностью определения через род и видовое отличие является генетическое определение, в котором указывается способ образования только данного предмета. Например: "кислотами называются сложные вещества, образующиеся из кислотных остатков и атомов водорода, способных замешаться атомами металлов или обмениваться на них": "коррозия металлов — это окислительно-восстановительный процесс, образующийся в результате окисления атомов металла". Много генетических определений в математике, к их числу относятся такие, как "цилиндр вращения", "конус вращения".
Определения через ближайший род и видовое отличие и генетические определения входят в класс реальных определений, ибо они определяю само понятие, например, "информатика", "треугольник", "кислота" и др. К явным относятся и номинальные определения. Последние дают определение термина, который обозначает понятие, или вводят знаки, заменяющие понятие (обычно в свой состав они включают слово "называется"). Они часто встречаются в математике. Например: "конус называется круговым, если основание его - круг"; "Прямая, соединяющая вершину конуса и центр основания, называется осью конуса". Номинальными определениями, вводяшими знаки, являются следующие: "g - ускорение свободно падающего тела", "m - масса тела", "знак v обозначает строгую дизъюнкцию" и т.п. В приведенных выше примерах определения (1). (3) — реальные, а определения (2), (4) и (5) — номинальные.
Чтобы определение было правильным, надо соблюдать следующие правила.
Правила явного определения. Ошибки, возможные в определении
Похожие работы
... , нет цивилизации). Таким образом, общество и культура возникли раньше, а цивилизация позже. За всю историю существования в условиях цивилизации человечество жило не более 2% времени. Цивилизация – определенная часть или степень развития культуры. Большинство исследователей предполагает развитие интеллекта и нравственности, степень и уровень очеловечивания народов. Прогресс культуры идет от ...
... мыслью и для себя и для других только через слово - устное и письменное. Благодаря языку мысли людей не теряются, а передаются в виде системы знаний из поколения в поколение. 5. Виды определений понятий Дадим определение понятию. Понятие – форма мышления, отражающая предметы в существенных признаках. Признаком предмета называется то, в чём предметы сходны ...
... определения, причем в правовых науках точное определение понятий имеет не только теоретическое, но и практическое значение. В самом деле, если, например, в уголовном праве не будет точных определений понятий «умысел», «соучастие», «вина», «неосторожность», «необходимая оборона» и т. д., то это может привести к ошибочному толкованию этих понятий, к неправильному пониманию отраженных в них явлений, ...
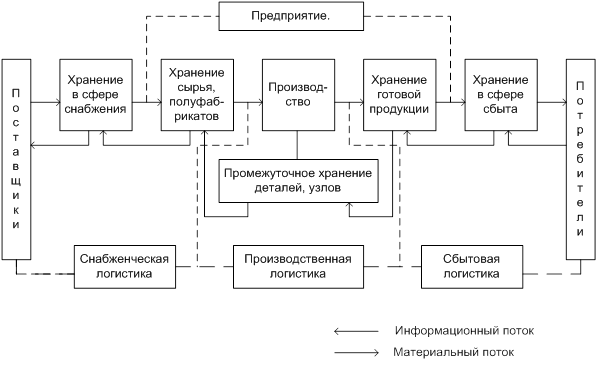
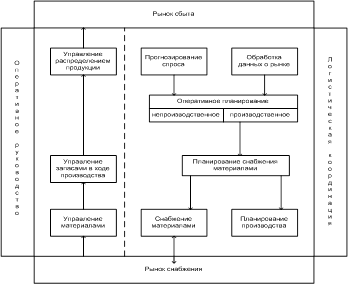
... возможностями закупки и производства. Выполнить эту задачу можно с помощью решения научных проблем развития самой логистики, начиная от структуризации технологии ее цепей и заканчивая различными локальными задачами. Функции логистики. В соответствии с современными задачами логистики различают два вида ее функций: оперативные и координационные. Оперативные функции связаны с непосредственным ...
0 комментариев