Навигация
2. Линейные пространства
Линейная зависимость и независимость векторов. Пусть Rn обозначает множество всех n-мерных векторов-строк. Заметим, что это не просто множество — Rn несет определенную структуру. Именно любой вектор Х∈ Rn можно умножить на любое число λX и результат — вектор λX есть снова элемент множества Rn. Сумма двух и даже любого конечного числа векторов из Rn снова есть элемент Rn. Кроме того, операции умножения вектора на число и сложения векторов связаны друг с другом определенными соотношениями (см. п. 2).
Во множестве Rn есть уникальный вектор 0 = (0, ..., 0). Его роль вполне аналогична роли числа 0 во множестве чисел. Так, 0·X = 0 и X + 0 = X для любого Х∈ Rn .
Вектор X, удовлетворяющий неравенству X > 0, называется неотрицательным. Неотрицательный вектор — это в точности тот, все компоненты которого неотрицательны. Вектор (2, 3) является неотрицательным, а вектор (-2, 4) — нет, ибо его 1-я компонента не является неотрицательным числом.
По всем этим причинам Rn называют n-мерным числовым (или арифметическим) линейным пространством. Слово «числовое» в названии линейного пространства подчеркивает, что элементами такого пространства являются векторы, компоненты которых есть числа.
Вектор В = (b1, …, bm) называется линейной комбинацией векторов A = (a11, …, am1), …, An = (a1n, …, amn) той же размерности, если найдутся числа х1, ..., хn такие, что В = x1A1 + ... + хnАn. Следовательно, чтобы узнать это, надо решить систему из m линейных алгебраических уравнений (СЛАУ) с n неизвестными:
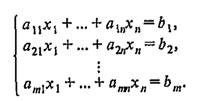
Узнаем, например, является ли вектор F = (1, 6) линейной комбинацией векторов H1 = (1, 2), H2 = (0, 2). Получаем совсем простую СЛАУ:
![]()
Ее решение: х1 = 1, х2 = 2. Следовательно, F = H1 + 2H2.
Система векторов называется линейно зависимой если какой-то вектор системы есть линейная комбинация остальных векторов системы, и линейно независимой в противном случае, т.е. когда никакой вектор системы не является линейной комбинацией остальных векторов системы.
Например, система из трех вышеприведенных векторов F1, H1, H2 линейно зависима, ибо F = H1 + 2H2
Пусть A — какая-нибудь система векторов, тогда ее подсистема ε называется базисом этой системы, если ε линейно независима, и любой вектор системы A есть линейная комбинация векторов из ε.
Пусть ε = (E1, …, En). Если B ∈ A, то B = λ1E1 +... + λnEn при некоторых λ1, …, λn
Линейная комбинация λ1E1 +... + λnEn называется разложением вектора В по векторам E1... En, а числа λ1, ..., λnназываются коэффициентами этого разложения.
Эти коэффициенты называются координатами вектора в базисе ε.
3. Пространство товаров, цены
Под товаром понимается некоторое благо или услуга, поступившие в продажу в определенное время и в определенном месте. Будем считать, что имеется n различных товаров, количество i-го товара обозначается хi тогда некоторый набор товаров обозначается X = = (x1,…, хn). Как известно, упорядоченный набор n чисел называется n-мерным вектором, так что X есть n-мерный вектор. Вообще-то набор товаров надо считать вектором-столбцом, но по соображениям экономии места будем изображать его вектором-строкой. Будем рассматривать, как правило, только неотрицательные количества товаров, так что хi ≥ 0 для любого i = 1, … ,n или Х≥ 0.
Множество всех наборов товаров называется пространством товаров С. Это множество называется пространством потому, что в нем можно сложить любые два набора и умножить любой набор товаров на любое неотрицательное число. Возможность умножения набора товаров на любое неотрицательное число отражает предположение о безграничной делимости и умножении товаров (т.е. товары устроены наподобие сахарного песка, а не авианосцев). Набор товаров можно трактовать, как корзину, в которой лежат эти товары в соответствующем количестве. Аналогично интерпретируются и операции с наборами товаров.
Решение потребителя о покупке определенного набора товаров математически - выбор конкретной точки в пространстве C.
Пример 2. Пространство товаров С представляет собой часть арифметического линейного пространства Rn — так называемый неотрицательный октант, С = {X ∈ Rn : X≥ 0}. Поэтому при работе с пространством товаров можно использовать структуру линейного пространства (соблюдая некоторые естественные ограничения). Так, для любого X Є С подмножество LX = {λX: 0 ≤ λ} называется лучом, проходящим через X; для любых двух точек X, Y любая точка αХ + βY ∈ С называется их линейной комбинацией, а множество [X, Y] = {αХ + βY: α, β ≥ 0, α + β = 1} называется отрезком, соединяющим X и Y. Подмножество W ≤ С является выпуклым, если вместе с любыми X,Y ∈ W весь соединяющий их отрезок лежит в W.
Предполагается, что каждый товар имеет цену. Все цены строго положительны. Пусть цена единицы i-го товара есть рi, тогда Р = (pi,…,рn) есть вектор-строка цен.
Для набора товаров X и вектора цен Р их скалярное произведение РХ = р1x1 + ... + рnxn есть число, называемое ценой набора X или его стоимостью, и будет обозначаться С(Х).
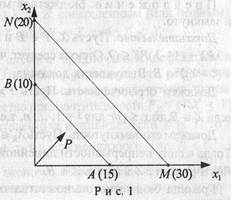
Пример 3. Отношение равной стоимости разбивает все пространство товаров на непересекающиеся классы (для случая двух товаров см. рис. 1). Пусть вектор цен есть (2, 3), тогда класс наборов стоимости 30 есть отрезок АВ, а стоимости 60 есть отрезок MN. Стрелка показывает направление увеличения стоимости наборов. В качестве этой стрелки можно взять вектор цен.
С обыденной точки зрения каждый товар должен быть желателен для участников экономики и должен обладать определенной потребительской полезностью. Это свойство товаров выражается в некоторой мере через цены на них.
Пусть вектор цен есть Р. Зафиксируем какую-нибудь денежную сумму Q и назовем ее доходом.
Множество наборов товаров стоимости не более Q при данных ценах Р называется бюджетным множеством В; множество наборов товаров стоимости ровно Q называется границей G этого бюджетного множества.
Бюджетное множество и его граница зависят от цен и дохода, так что точнее их было бы обозначать В(Р, Q) и G(P, Q).
Бюджетное множество и его границу можно определить так:
с помощью обычных неравенств и равенств —
В(Р, Q) = {(x1, ..., хn): х1 …, хn ≥ 0, p1x1 + ... + pnxn ≤Q)
G(P, Q) = {(x1, ..., хn): х1 …, хn ≥ 0, p1x1 + ... + pnxn = Q);
с помощью векторных неравенств и равенств —
В(Р, Q) = {Х:Х> О, РХ< 0 , G{P, Q) = {Х:Х> О, РХ= Q).
Для случая двух товаров см. рис. 1.
При Р = (2, 3) и Q = 30 бюджетное множество В(Р, Q) есть треугольник ОАВ, точка A имеет координату Q/p1 = 15, точка В — Q/p2 = 30. Отрезок АВ есть граница бюджетного множества, отрезок АВ перпендикулярен вектору цен. При увеличении Q граница бюджетного множества движется в направлении вектора цен. При изменении цен об изменении бюджетного множества можно судить по движению точек А(р1) = Q/p1, B(p2) = Q/p2.
Бюджетное множество выпукло, ограниченно и замкнуто.
Граница бюджетного множества также есть выпуклое, ограниченное и замкнутое множество.
Похожие работы
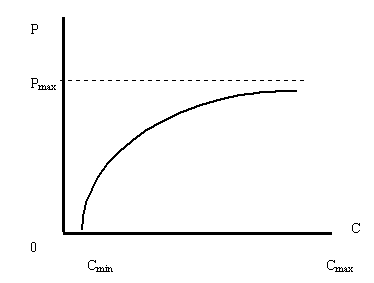
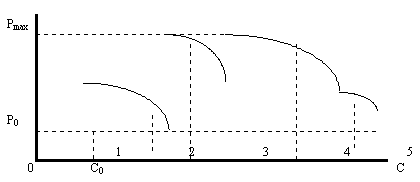
... обозначить как Cmin. Дальнейшее увеличение дохода у потребителя приводит к тому, что при данной фиксированной цене покупается уже большее количество товара. Какой же характер имеет зависимость граничной цены от величины минимального дохода Cmin? Приведу несколько гипотез и предложений на них основанных. Пусть доход покупателя равен нулю, то есть у него нет ни одной копейки. Очевидно, что в ...
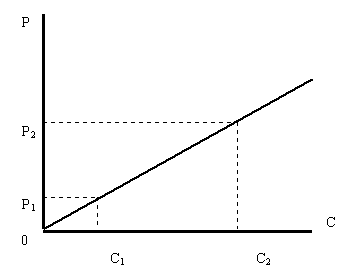
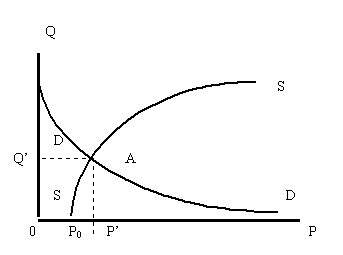
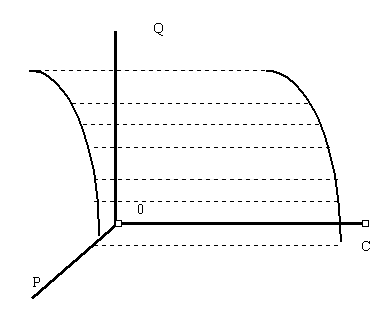
... на плоскости получалась только точка рыночного равновесия. Взаимосвязь между общеизвестной равновесной точкой и предлагаемой мною равновесной кривой очевидна. При фиксированном доходе на кривой рыночного равновесия, расположенной в пространстве, фиксируется одна и только одна точка. Легко показать, что при фиксированном доходе плоскость, секущая поверхности спроса и предложения и проходящая через ...
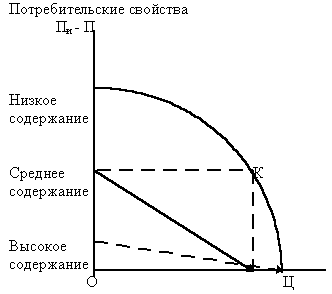
... столкнуться с целым рядом проблем, к которым следует подготовиться заранее. Первая проблема, которую следует признать довольно легко решаемой - это проблема размерностей используемых в модели составляющих. Потребительские свойства товара не имеют какой-либо размерности. В лучшем случае можно вспомнить из экономической теории такую размерность как <ютили> - единицы полезности. Впрочем, эти ...
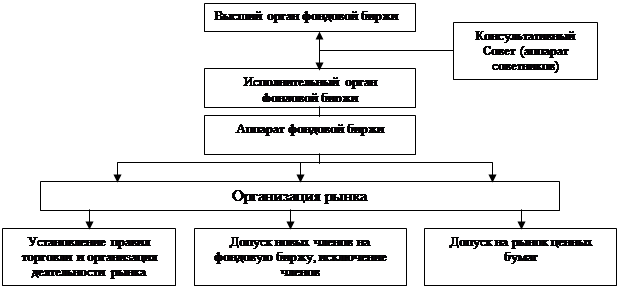
... и нормативно-правовой базы, создан развитый инструментарий, появились различные категории участников рынка, объединения профессиональных участников. Вместе с тем развитие рынка ценных бумаг в России столкнулось, особенно в последние два года, с серьёзными трудностями. По мнению Национальной ассоциации участников фондового рынка (НАУФОР), "привлечение инвестиций предприятия оставалось наиболее ...




0 комментариев