ЗАДАЧА 1
Составить модель оптимального выпуска продукции для цеха кондитерской фабрики. Виды выпускаемой продукции (М), виды основного сырья (П) и его запасы, нормы расхода сырья на единицу, уровни прибыли приведены в таблице. Рассчитать план и провести его анализ.
| Виды сырья | Расходы сырья на единицу продукции | Общий запас сырья, ед. | |||
| М1 | М2 | М3 | |||
| П1 | 2 | 4 | 3 | 266 |
|
| П2 | 1 | 3 | 4 | 200 |
|
| П3 | 3 | 2 | 1 | 303 |
|
| Уровень прибыли на ед. продукции | 20 | 24 | 28 |
| |
Содержание задачи.
Цех кондитерской фабрики вырабатывает три ассортиментные группы конфет, условно обозначенные М1, М2, М3 /в ед./.
Для их производства используются основные виды ресурсов /сырья/ трех видов, условно названных П1, П2, П3 /в ед./.
Расход каждого ресурса на производство единицы продукции является заданной величиной, определяется по рецептуре и обозначается символами а11, a12..., а33, где а - норма расхода, первая подстрочная 1 – номер ресурса, вторая подстрочная 1, 2, 3 – номер ассортиментной группы конфет.
Наличие каждого ресурса для производства всех, групп конфет принимается как известная величина и обозначается символами в1, в2, в3.
Прибыль на продукцию также принимается как известная величина и обозначается символами c1, c2, с3.
Перечисленные параметры являются величинами известными и выражаются в единых единицах измерения, кроме прибыли. Прибыль или другой какой показатель, являющийся критерием оптимальности, выражается в единицах измерения дохода /например, прибыли/, получаемого от производства единицы продукции в денежном или другом каком-нибудь выражении.
Поскольку решение задачи заключается в поиске такого плана производства, который обеспечивал бы в принятых условиях наибольший доход, принимаются те величины, которые являются неизвестными и обозначающими количества каждой группы конфет, включаемых в план производства: x1 для M1; х2 для М2; х3 для М3.
Экономико-математическая модель в символическом виде.
Система ограничений
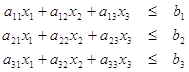
Целевая функция /суммарный доход/ F = с1х1 + с2х2 + с3х3 = мах
Условия неотрицательности неизвестных х1 ≥ 0, х2 ≥ 0, х3 ≥ 0
Символическая модель, наполненная численной информацией, будет иметь следующий вид:
2x1 + 4x2 + 3x3 ≤ 266
1x1 + 3x2 + 4x3 ≤ 200
3x1 + 2x2 + 1x3 ≤ 303
Прибыль от реализации выпускаемой продукции должна быть максимальной, то есть F = 20х1 + 24х2 + 28х3 = max;
Решение задачи.
Для решения задачи симплексным методом неравенства преобразуются в эквивалентные равенства путем добавления в каждое неравенство по одному дополнительному неизвестному с коэффициентом + 1 и нулевым уравнением прибыли. Для удобства расчетов левые и правые части уравнений меняются местами. В этом случае исходные неравенства примут вид симплексных уравнений:
266 = 2x1 + 4x2 + 3x3 + 1x4
200 = 1x1 + 3x2 + 4x3 + 1x5
303 = 3x1 + 2х2 + 1x3 + 1x6
F = 20х1 + 24х2 + 28х3 + 0x4 + 0x5 + 0x6
Коэффициенты при неизвестных записываются в симплексной таблице, в которой выполняются расчеты и отражаются полученные результаты.
Исходная таблица
| cj | p0 | x0 | 20 | 24 | 28 | 0 | 0 | 0 |
| x1 | х2 | х3 | х4 | х5 | х6 | |||
| 0 | х4 | 266 | 2 | 4 | 3 | 1 | 0 | 0 |
| 0 | х5 | 200 | 1 | 3 | 4 | 0 | 1 | 0 |
| 0 | х6 | 303 | 3 | 2 | 1 | 0 | 0 | 1 |
| Zj - Cj | 0 | -20 | -24 | -28 | 0 | 0 | 0 | |
В столбцах таблицы записывают: в первом (Cj) – прибыль единицы продукции, которая вводится в план выпуска; во втором (Р0) – неизвестные, включаемые в план; в третьем (Х0) – свободные величины; в остальных – коэффициенты при неизвестных уравнений. В верхней части этих столбцов отражаются коэффициенты при неизвестных целевой функции.
В нижней строке (целевой) записываются получаемые расчетным путем показатели: в столбце х0 – суммарная прибыль планового выпуска, в остальных столбцах – прибыль единицы продукции с отрицательным знаком.
В последних трех столбцах коэффициенты при дополнительных неизвестных, равные единице, расположены по диагонали. Эта часть таблицы, называемая единичной подматрицей, необходима для вычислительных и аналитических целей.
При решении задач на максимум целевой функции наличие в целевой строке отрицательных чисел указывает на возможность начала или продолжения решения задачи. Порядок решения таков: из отрицательных чисел целевой строки выбирается наибольшее по модулю. Столбец, в котором оно находится, принимается за ключевой (или разрешающий) и для удобства расчетов выделяется. В нашем примере таким столбцом будет Х3, имеющий в целевой строке наибольшую по модулю величину -28.
1-ая итерация
| cj | p1 | x0 | x1 | х2 | х3 | х4 | х5 | х6 |
| 0 | х4 | 116 | 1.3 | 1.75 | 0 | 1 | -1 | 0 |
| 28 | х3 | 50 | 0.3 | 0.75 | 1 | 0 | 0.3 | 0 |
| 0 | х6 | 253 | 2.8 | 1.25 | 0 | 0 | -0 | 1 |
| Zj - Cj | 1400 | -13 | -3 | 0 | 0 | 7 | 0 | |
Затем элементы столбца Х0 (свободные величины) делят на соответствующие коэффициенты ключевого столбца и полученные результаты сопоставляют между собой. Строка с наименьшим отношением принимается за ключевую и также для удобства выделяется. В нашем случае 266/3 = 88,7; 200/4 = 50; 303/1 = 303. Наименьшее отношение 50 имеет срока х5, она и будет ключевой. Ключевой элемент 4.
Далее элементы таблицы преобразуются и записываются в новую таблицу. Первоначально преобразуют элементы ключевой строки путем деления их на ключевой элемент. Преобразованные элементы записывают в том же самом месте.
В столбцах Ро и Cj занимают место вводимая в план неизвестная х3 с прибылью 28 (итерация 1-я). Остальные элементы преобразуются по следующему правилу:
- для преобразуемого элемента в его столбце находят элемент ключевой строки, а в его строке - элемент ключевого столбца;
- соответствующие элементы ключевой строки и ключевого столбца перемножаются и полученное произведение делят на ключевой момент;
- частное от деления вычитают из значения элемента, которое он имел до преобразования, и полученный результат будет преобразованным элементом, который записывается в новую таблицу в том же самом месте. Следуя этому правилу, преобразование элементов столбца х0 будет:
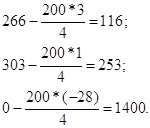
Включение на первой итерации в план неизвестной х3 обеспечит сумму прибыли 1400 руб.
Решение задачи продолжается, так как в целевой строке два отрицательных элемента. Наибольший по модулю элемент -13. Он находится в столбце х1, который принимается за ключевой, а ключевой строкой будет х6 (116:1,3=92,8; 50:0,3=200; 253:2,8=92), ключевым элементом 2,8. Элементы таблицы преобразуются в том же порядке по изложенному правилу и записываются в новую таблицу.
2-я итерация
| cj | p2 | x0 | x1 | х2 | х3 | х4 | х5 | х6 |
| 0 | х4 | 1 | 0 | 1.18 | 0 | 1 | -1 | -0.5 |
| 28 | х3 | 27 | 0 | 0.64 | 1 | 0 | 0.3 | -0.1 |
| 13 | х1 | 92 | 1 | 0 | 0 | 0 | 0 | 0 |
| Zj - Cj | 2596 | 0 | 2.91 | 0 | 0 | 5.8 | 4.7 | |
В последней таблице целевая строка имеет только положительные элементы. Это значит, что составленный план оптимален и дальнейшее улучшение его невозможно.
Как видно из таблицы, оптимальный план предусматривает выпуск продукции П1 27 ед. (х1 = 27), П3 92 ед. (х3 = 92), дополнительного неизвестного П4 1 ед. (х4 = 1). П2 и дополнительные неизвестные в план не вошли, следовательно, х2 = 0, х5 = 0 х6 = 0. Подставив значения неизвестных в уравнения, получим:
2 * 92 + 4 * 0 + 3 * 27 + 1 = 266
1 * 92 + 3 * 0 + 4 * 27 + 0 = 200
3 * 92 + 2 * 0 + 1 * 27 + 0 = 303
F = 20 * 92 + 24 * 0 + 27 * 28 = 2596
Анализ оптимального плана.
а) Запасы сырья трех видов используются не полностью, так как х4 = 1, а х5 = х6 = 0.
б) Рассмотрим элементы матрицы.
От выпуска продукции II следует отказаться.
Элементы столбца х5 показывают, что увеличение запасов сахара на I ед. (х5 = 1) позволит увеличить выпуск продукции III вида на 0,3 ед. Сумма прибыли увеличится на 5,8 руб.
Элементы столбца х6 показывают, что увеличение запасов жира на I ед. (х6 = 1) позволит уменьшить выпуск только продукции III вида на 0,1 ед. (27 - 0.1) Сумма прибыли увеличится на 4,7 руб.
Снижение запасов сырья приводит к изменениям выпуска продукции и суммы прибыли в обратном порядке.
Элементы целевой строки оптимального плана называются двойственными оценками, которые определяют величину изменения прибыли при изменении запасов сырья на I ед.
ЗАДАЧА 2
Требуется определить минимальную по стоимости смесь сырья для изготовления пищевых концентратов, которые должны содержать питательные вещества (П). Эти вещества содержаться в сырье (М) в различных сочетаниях. Содержание питательных веществ в сырье и готовом продукте, а также цена на каждый вид сырья показаны в таблице.
| Питательные вещества | Виды сырья | Минимальное содержание (единиц) питательных веществ в готовом продукте | ||
| M1 | М2 | М3 | ||
| П1 | 1 | 1 | 0 | 50 |
| П2 | 4 | 1 | 3 | 140 |
| П3 | 1 | 4 | 1 | 127 |
| П4 | 0 | 3 | 2 | 80 |
| Цена за единицу сырья, руб. | 8 | 12 | 10 | |
Виды используемого сырья условно обозначены через М1, М2, М3; содержание питательных веществ в сырье и готовом продукте обозначены П1, П2, П3, П3.
Исходные условия задачи выражаются неравенствами:
1х1 + 1х2 + 0х3 ≥ 50
4х1 + 1х2 + 3х3 ≥ 140
1х1 + 4х2 + 1х3 ≥ 127
0х1 + 3х2 + 2х3 ≥ 80
F = 8х1 + 12х2 + 10х3 = min
Умножив обе части неравенств на -1, получим систему с другим направлением знака неравенств:
-1х1 - 1х2 - 0х3 ≥ -50
-4х1 - 1х2 - 3х3 ≥ -140
-1х1 - 4х2 - 1х3 ≥ -127
0х1 - 3х2 - 2х3 ≥ -80
F = 8х1 + 12х2 + 10х3 = min
Преобразуем неравенства в эквивалентные равенства с помощью дополнительных неизвестных. Симплексные уравнения будут следующими:
-50 = -1х1 - 1х2 - 0х3 + 1х4 + 0х5 + 0х6 + 0х7
-140 = -4х1 - 1х2 - 3х3 + 0х4 + 1х5 + 0х6 + 0х7
-127 = -1х1 - 4х2 - 1х3 + 0х4 + 0х5 + 1х6 + 0х7
-80 = 0х1 - 3х2 - 2х3 + 0х4 + 0х5 + 0х6 + 1х7
F = 8х1 + 12х2 + 10х3 + 0х4 + 0х5 + 0х6 + 0х7 = min
Записанные уравнения отличаются от тех, которые нами рассматривались выше, тем, что коэффициенты при основных неизвестных и свободные члены имеют отрицательные знаки.
Решение таких задач производится двойственным симплексным методом. Система симплексных уравнений записывается в таблице.
| cj | p0 | x0 | 8 | 12 | 10 | 0 | 0 | 0 | 0 |
| x1 | х2 | х3 | х4 | х5 | х6 | х7 | |||
| 0 | х4 | -50 | -1 | -1 | 0 | 1 | 0 | 0 | 0 |
| 0 | х5 | -140 | -4 | -1 | -3 | 0 | 1 | 0 | 0 |
| 0 | х6 | -127 | -1 | -4 | -1 | 0 | 0 | 1 | 0 |
| 0 | х7 | -80 | 0 | -3 | -2 | 0 | 0 | 0 | 1 |
| Zj - Cj | 0 | -8 | -12 | -10 | 0 | 0 | 0 | 0 | |
Элементы целевой строки рассчитывают по обычным правилам и получают отрицательные знаки.
В отличие от вычислительной процедуры основного симплексного метода решение задач двойственным методом выполняется в обратном порядке.
В итоговом столбце свободные числа имеют отрицательные знаки. Это является свидетельством того, что данный план нельзя считать допустимым, так как он противоречит экономическому смыслу. План можно считать допустимым только тогда, когда в итоговом столбце не будет отрицательных чисел.
Ликвидация отрицательных чисел в итоговом столбце начинается с наибольшего по абсолютной величине. В нашем примере таким числом является (-140). Строка х5, в которой находится это число, принимается за ключевую и соответственно выделяется.
Определив ключевую строку, находим ключевой столбец. Для этого нужно элементы целевой строки разделить на элементы ключевой строки и из полученных отношений выбрать наименьшее. Столбец, имеющий наименьшее отношение, принимается за ключевой и так же как ключевая строка, выделяется.
Столбцы х1, х2, х3 будут иметь следующие отношения:
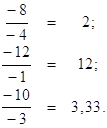
Наименьшее отношение имеет столбец х1, он и будет являться ключевым.
Определив ключевую строку, ключевой столбец и ключевое число, по обычным правилам преобразуются все элементы матрицы и записываются в новой таблице.
1-я итерация
| cj | p0 | x0 | 18 | 15 | 24 | 0 | 0 | 0 | 0 |
| x1 | х2 | х3 | х4 | х5 | х6 | х7 | |||
| 0 | х4 | -15 | 0 | -0.75 | 0.75 | 1 | -0.25 | 0 | 0 |
| 8 | х1 | 35 | 1 | 0.25 | 0.75 | 0 | -0.25 | 0 | 0 |
| 0 | х6 | -92 | 0 | -3.75 | -0.25 | 0 | -0.25 | 1 | 0 |
| 0 | х7 | -80 | 0 | -3 | -2 | 0 | 0 | 0 | 1 |
| Zj - Cj | 280 | 0 | -10 | -4 | 0 | -2 | 0 | 0 | |
После преобразования элементов в итоговом столбце осталось еще три отрицательных числа в строке х4, х6 и х7. Наибольшим по абсолютной величине является число в строке х6. Эта строка будет принята за ключевую для последующего расчета. Ключевой столбец определяется по наименьшему отношению элементов целевой строки к элементам ключевой строки. Им будет столбец х2. Вводим этот вид сырья в программу вместо неизвестного х6. По общим правилам преобразуем элементы матрицы.
2-я итерация
| cj | p0 | x0 | x1 | х2 | х3 | х4 | х5 | х6 | х7 |
| 0 | х4 | 3.4 | 0 | 0 | 0.8 | 1 | -0.2 | -0.2 | 0 |
| 8 | х1 | 28.9 | 1.0 | 0.0 | 0.7 | 0.0 | -0.3 | 0.1 | 0.0 |
| 15 | х2 | 24.5 | 0.0 | 1.0 | 0.1 | 0.0 | 0.1 | -0.3 | 0.0 |
| 0 | х7 | -6.4 | 0.0 | 0.0 | -1.8 | 0.0 | 0.2 | -0.8 | 1.0 |
| Zj - Cj | 525.3 | 0.0 | 0.0 | -3.3 | 0.0 | -1.3 | -2.7 | 0.0 | |
После преобразования элементов в итоговом столбце осталось еще одно отрицательное число в строке х7. Эта строка будет принята за ключевую для последующего расчета. Ключевой столбец определяется по наименьшему отношению элементов целевой строки к элементам ключевой строки. Им будет столбец х3. Вводим этот вид сырья в программу вместо неизвестного х7. По общим правилам преобразуем элементы матрицы.
В таблице записаны преобразованные числа, полученные на 3-й итерации. В итоговом столбце все отрицательные числа исчезли, значит полученный план является допустимым и одновременно оптимальным. Вывод о том, что план получен оптимальный, позволяют сделать элементы целевой строки. Все они отрицательны или равны нулю, что свидетельствует об оптимальности результата при решении задач на минимум целевой функции.
3-я итерация
| cj | p0 | x0 | x1 | х2 | х3 | х4 | х5 | х6 | х7 |
| 0 | х4 | 0.6 | 0.0 | 0.0 | 0.0 | 1.0 | -0.1 | -0.6 | 0.4 |
| 8 | х1 | 26.3 | 1.0 | 0.0 | 0.0 | 0.0 | -0.2 | -0.3 | 0.4 |
| 15 | х2 | 24.3 | 0.0 | 1.0 | 0.0 | 0.0 | 0.1 | -0.3 | 0.0 |
| 10 | х3 | 3.6 | 0.0 | 0.0 | 1.0 | 0.0 | -0.1 | 0.4 | -0.6 |
| Zj - Cj | 537.2 | 0.0 | 0.0 | 0.0 | 0.0 | -1.7 | -1.2 | -1.9 | |
Подставив значения неизвестных в исходные неравенства, получаем:
1 * 26,3 + 1 * 24,3 + 0 * 3,6 ≥ 50
4 * 26,3 + 1 * 24,3 + 3 * 3,6 ≥ 140
1 * 26,3 + 4 * 24,3 + 1 * 3,6 ≥ 127
0 * 26,3 + 3 * 24,3 + 2 * 3,6 ≥ 80
Стоимость сырья при этом будет минимальной и составит:
F = 8 * 26,3 + 12 * 24,3 + 12 * 3,6 = 537,2
ЗАДАЧА 3
Составить оптимальный план перевозок пищевых продуктов от 4-х поставщиков к 6-ти потребителям. Поставщики (П), потребители (М), объемы вывоза и завоза, кратчайшие расстояния между пунктами вывоза и завоз приведены в таблице.
| Поставщики | Потребители | Объемы вывоза, т | |||||
| М1 | М2 | М3 | М4 | М5 | М6 | ||
| П1 | 24 | 30 | 42 | 15 | 39 | 21 | 144 |
| П2 | 9 | 24 | 30 | 33 | 27 | 29 | 148 |
| П3 | 24 | 22 | 20 | 45 | 21 | 23 | 76 |
| П4 | 11 | 36 | 27 | 40 | 30 | 8 | 132 |
| Объемы завоза, т | 92 | 84 | 80 | 112 | 96 | 36 | |
Решение задачи начинается с распределения у имеющихся у поставщиков объемов вывоза между потребителями с учетом объемов завоза. Для первоначального распределения используются способы: северо-западного угла, наименьшего элемента по строке, наименьшего элемента по столбцу, наименьшего элемента матрицы.
Способ северо-западного угла состоит в том, что распределение объемов вывоза производится, начиная с верхнего левого угла таблицы и кончая нижним углом ее. Результаты распределения показаны в таблице.
| Поставщики и объемы вывоза, т | Потребители и объемы завоза | Потенциалы строк | ||||||
| М1 | М2 | М3 | М4 | М5 | М6 | |||
| 92 | 84 | 80 | 112 | 96 | 36 | |||
| П1 | 144 | 24 | 30 | 42 | 15 | 39 | 21 | 0 |
| 92 | 52 | |||||||
| П2 | 148 | 9 | 24 | 30 | 33 | 27 | 29 | -6 |
| 32 | 80 | 36 | ||||||
| П3 | 76 | 24 | 22 | 20 | 45 | 21 | 23 | 6 |
| 76 | 0 | |||||||
| П4 | 132 | 11 | 36 | 27 | 40 | 30 | 8 | 15 |
| 96 | 36 | |||||||
| Потенциалы столбцов | 24 | 30 | 36 | 39 | 15 | -7 | ||
Проверка плана на оптимальность. Когда исходный план получен и рассчитана соответствующая ему суммарная тонно-километровая работа, определяют, является ли этот план оптимальным. Для проверки плана на оптимальность применяется метод потенциалов.
Сущность метода потенциалов состоит в том, что для каждой строки и каждого столбца таблицы (матрицы) определяют специальные числа, называемые потенциалами. С помощью этих потенциалов можно установить, нужно ли заполнять свободную клетку матрицы или ее нужно оставить незаполненной.
Для решения задач методом потенциалов исходный план должен иметь количество заполненных клеток m + n – 1 (m - число строк, n - число столбцов). Если план не отвечает этим требованиям, то не для всех строк и столбцов можно рассчитать потенциалы, а без них нельзя проверить план на оптимальность.
Потенциалы строк и столбцов определяются по заполненным клеткам, находящимся на их пересечении.
Элемент заполненной клетки должен равняться сумме потенциалов строки и столбца, на пересечении которых находится эта заполненная клетка.
Для начала вычислений первый потенциал для строки или столбца принимается условно равным нулю, все остальные потенциалы определяются с помощью элементов заполненных клеток.
Обозначив потенциалы строк ui, потенциалы столбцов Vj, элементы заполнения клеток ![]() , можно записать порядок расчета потенциалов для общего случая.
, можно записать порядок расчета потенциалов для общего случая.
Из основного требования ![]() = ui+ Vj вытекает:
= ui+ Vj вытекает:
ui = ![]() - Vj; Vj =
- Vj; Vj = ![]() - ui
- ui
Из этих выражений видно, что для расчета потенциала строки необходимо иметь заполненную клетку, в столбце которой потенциал уже определен, а для расчета потенциала столбца нужна заполненная клетка, имеющая потенциал в строке.
Потенциалы показаны в таблице.
После того, как по строкам и столбцам определены потенциалы, с их помощью выясняется, является ли план оптимальным, и если нет, то как его можно улучшить. С этой целью для каждой свободной клетки вычисляется сумма потенциалов строк и столбцов, на пересечении которых находится эта клетка.
Сравнение суммы потенциалов с величиной элемента в свободных клетках позволяет определить, нужно ли заполнять эту клетку или ее нужно оставить свободной.
При решении задач на минимум функционала (в нашем случае на минимум тонно-километровой работы) не заполняются те свободные клетки, в которых сумма потенциалов меньше величины элемента (в нашем случае - расстояния).
Иными словами, если характеристика, значение которой равно разности ![]() - (ui+ Vj), положительная, то свободная метка не заполняется при решении задачи на минимум функции.
- (ui+ Vj), положительная, то свободная метка не заполняется при решении задачи на минимум функции.
Свободные клетки, имеющие нулевое значение характеристики, показывают на то, что их заполнение приведет к перераспределению поставок, но объем работ (значение функционала) останется неизменным.
Суммы потенциалов, значения элементов и характеристики для незаполненных клеток приведены в таблице.
| Шифры клеток | П1-М3 | П1-М4 | П1-М5 | П1-M6 | П2-М1 | П2-М5 | П2-М6 | П3-М1 | П3-М2 | П3-М3 | П3-М6 | П4-М1 | П4-М2 | П4-М3 | П4-М4 |
| Суммы потенциалов | 36 | 39 | 15 | -7 | 18 | 9 | -13 | 30 | 36 | 42 | -1 | 39 | 45 | 51 | 54 |
| Значение элементов | 42 | 15 | 39 | 21 | 9 | 27 | 29 | 24 | 22 | 20 | 23 | 11 | 36 | 27 | 40 |
| Характеристики | 6 | -24 | 24 | 28 | -9 | 18 | 42 | -6 | -14 | -22 | 24 | -28 | -9 | -24 | -14 |
В первоначальном плане шесть клеток имеют положительные характеристики, в девяти клетках характеристики отрицательные.
Так как задача решается на минимум целевой функции, то именно эти отрицательные клетки должны быть заполнены поставщиками. Но заполнение свободной клетки и связанное с ним перераспределение поставок производится не изолированно, а в связи с несколькими заполненными клетками. Эта связь выявляется путем построения замкнутых многоугольников, вершинами которых являются клетки таблицы. Одна вершина многоугольника находится в свободной клетке, а все остальные - в заполненных клетках. Многоугольник, или как его называют цепь, имеет прямые углы и четное число вершин.
В результате перераспределения в каждой вершине (клетке) цепи происходит изменение величины поставок: в одних клетках они увеличиваются, в других - уменьшаются.
Те клетки цепи, у которых поставки увеличиваются, называются положительными, а те, у которых поставки уменьшаются - отрицательными. Каждая цепь имеет одинаковое число положительных и отрицательных вершин (клеток). Положительные и отрицательные вершины чередуются. Если свободную клетку, в которую предполагается произвести запись, принять как положительную (поскольку изменение произойдет в сторону увеличения), то следующая клетка будет отрицательной, затем опять положительной, снова отрицательной, и т.д.
Из свободных клеток для заполнения выбирают обычно клетку, которая имеет наибольшую отрицательную характеристику. В нее записывают самую наименьшую величину из отрицательных вершин цепи.
+П4М1 -П1М1 +П1М2 -П2М2 +П2М4 -П3М4 +П3М5 -П4М5
| Поставщики и объемы вывоза, т | Потребители и объемы завоза | Потенциалы строк | ||||||
| М1 | М2 | М3 | М4 | М5 | М6 | |||
| 92 | 84 | 80 | 112 | 96 | 36 | |||
| П1 | 144 | 24 | 30 | 42 | 15 | 39 | 21 | 0 |
| 60 | 84 | |||||||
| П2 | 148 | 9 | 24 | 30 | 33 | 27 | 29 | -6 |
| 80 | 68 | |||||||
| П3 | 76 | 24 | 22 | 20 | 45 | 21 | 23 | 6 |
| 44 | 32 | |||||||
| П4 | 132 | 11 | 36 | 27 | 40 | 30 | 8 | 15 |
| 32 | 64 | 36 | ||||||
| Потенциалы столбцов | 24 | 30 | 36 | 39 | 15 | -7 | ||
| Шифры клеток | П1-М3 | П1-М4 | П1-М5 | П1-М6 | П2-М1 | П2-М2 | П2-М5 | П2-М6 | П3-М1 | П3-М2 | П3-М3 | П3-М6 | П4-М2 | П4-М3 | П4-М4 |
| Суммы потенциалов | 36 | 39 | 15 | -7 | 18 | 24 | 9 | -13 | 30 | 36 | 42 | -1 | 45 | 51 | 54 |
| Значение элементов | 42 | 15 | 39 | 21 | 9 | 24 | 27 | 29 | 24 | 22 | 20 | 23 | 36 | 27 | 40 |
| Характеристики | 6 | -24 | 24 | 28 | -9 | 0 | 18 | 42 | -6 | -14 | -22 | 24 | -9 | -24 | -14 |
+П2М5 -П4М5 +П4М1 -П1М1 +П1М4 -П2М4
| Поставщики и объемы вывоза, т | Потребители и объемы завоза | Потенциалы строк | ||||||
| М1 | М2 | М3 | М4 | М5 | М6 | |||
| 92 | 84 | 80 | 112 | 96 | 36 | |||
| П1 | 144 | 24 | 30 | 42 | 15 | 39 | 21 | 0 |
| 16 | 84 | 44 | ||||||
| П2 | 148 | 9 | 24 | 30 | 33 | 27 | 29 | 18 |
| 80 | 68 | |||||||
| П3 | 76 | 24 | 22 | 20 | 45 | 21 | 23 | -22 |
| 76 | ||||||||
| П4 | 132 | 11 | 36 | 27 | 40 | 30 | 8 | -13 |
| 76 | 20 | 36 | ||||||
| Потенциалы столбцов | 24 | 30 | 12 | 15 | 43 | 21 | ||
| Шифры клеток | П1-М3 | П1-М5 | П1-М6 | П2-М1 | П2-М2 | П2-М5 | П2-М6 | П3-М1 | П3-М2 | П3-М3 | П3-М4 | П3-М6 | П4-М2 | П4-М3 | П4-М4 |
| Суммы потенциалов | 12 | 43 | 21 | 42 | 48 | 61 | 39 | 2 | 8 | -10 | -7 | -1 | 17 | -1 | 2 |
| Значение элементов | 42 | 39 | 21 | 9 | 24 | 27 | 29 | 24 | 22 | 20 | 45 | 23 | 36 | 27 | 40 |
| Характеристики | 30 | -4 | 0 | -33 | -24 | -34 | -10 | 22 | 14 | 30 | 52 | 24 | 19 | 28 | 38 |
+П2М5 -П4М5 +П4М1 -П1М1 +П1М4 -П2М4
| Поставщики и объемы вывоза, т | Потребители и объемы завоза | Потенциалы строк | ||||||
| М1 | М2 | М3 | М4 | М5 | М6 | |||
| 92 | 84 | 80 | 112 | 96 | 36 | |||
| П1 | 144 | 24 | 30 | 42 | 15 | 39 | 21 | 0 |
| 84 | 60 | |||||||
| П2 | 148 | 9 | 24 | 30 | 33 | 27 | 29 | 18 |
| 80 | 52 | 16 | ||||||
| П3 | 76 | 24 | 22 | 20 | 45 | 21 | 23 | 12 |
| 76 | ||||||||
| П4 | 132 | 11 | 36 | 27 | 40 | 30 | 8 | 21 |
| 92 | 4 | 36 | ||||||
| Потенциалы столбцов | -10 | 30 | 12 | 15 | 9 | -13 | ||
| Шифры клеток | П1-М1 | П1-М3 | П1-М5 | П1-М6 | П2-М1 | П2-М2 | П2-М6 | П3-М1 | П3-М2 | П3-М3 | П3-М4 | П3-М6 | П4-М2 | П4-М3 | П4-М4 |
| Суммы потенциалов | -10 | 12 | 9 | -13 | 8 | 30 | 5 | 2 | 42 | 24 | 27 | -1 | 51 | 33 | 36 |
| Значение элементов | 24 | 42 | 39 | 21 | 9 | 24 | 29 | 24 | 22 | 20 | 45 | 23 | 36 | 27 | 40 |
| Характеристики | 34 | 30 | 30 | 34 | 1 | -6 | 24 | 22 | -20 | -4 | 18 | 24 | -15 | -6 | 4 |
+П3М2 -П1М2 +П1М4 -П2М4 +П2М5 -П3М5
| Поставщики и объемы вывоза, т | Потребители и объемы завоза | Потенциалы строк | ||||||
| М1 | М2 | М3 | М4 | М5 | М6 | |||
| 92 | 84 | 80 | 112 | 96 | 36 | |||
| П1 | 144 | 24 | 30 | 42 | 15 | 39 | 21 | 0 |
| 32 | 112 | |||||||
| П2 | 148 | 9 | 24 | 30 | 33 | 27 | 29 | -2 |
| 80 | 68 | |||||||
| П3 | 76 | 24 | 22 | 20 | 45 | 21 | 23 | -8 |
| 52 | 24 | |||||||
| П4 | 132 | 11 | 36 | 27 | 40 | 30 | 8 | 1 |
| 92 | 4 | 36 | ||||||
| Потенциалы столбцов | 10 | 30 | 32 | 15 | 29 | 7 | ||
| Шифры клеток | П1-М1 | П1-М3 | П1-М5 | П1-М6 | П2-М1 | П2-М2 | П2-М4 | П2-М6 | П3-М1 | П3-М3 | П3-М4 | П3-М6 | П4-М2 | П4-М3 | П4-М4 |
| Суммы потенциалов | 10 | 32 | 29 | 7 | 8 | 28 | 13 | 5 | 2 | 24 | 7 | -1 | 31 | 33 | 16 |
| Значение элементов | 24 | 42 | 39 | 21 | 9 | 24 | 33 | 29 | 24 | 20 | 45 | 23 | 36 | 27 | 40 |
| Характеристики | 14 | 10 | 10 | 14 | 1 | -4 | 20 | 24 | 22 | -4 | 38 | 24 | 5 | -6 | 24 |
+П4М3 -П2М3 +П2М5 -П4М5
| Поставщики и объемы вывоза, т | Потребители и объемы завоза | Потенциалы строк | ||||||
| М1 | М2 | М3 | М4 | М5 | М6 | |||
| 92 | 84 | 80 | 112 | 96 | 36 | |||
| П1 | 144 | 24 | 30 | 42 | 15 | 39 | 21 | 0 |
| 32 | 112 | |||||||
| П2 | 148 | 9 | 24 | 30 | 33 | 27 | 29 | -2 |
| 76 | 72 | |||||||
| П3 | 76 | 24 | 22 | 20 | 45 | 21 | 23 | -8 |
| 52 | 24 | |||||||
| П4 | 132 | 11 | 36 | 27 | 40 | 30 | 8 | -5 |
| 92 | 4 | 36 | ||||||
| Потенциалы столбцов | 16 | 30 | 32 | 15 | 29 | 13 | ||
| Шифры клеток | П1-М1 | П1-М3 | П1-М5 | П1-М6 | П2-М1 | П2-М2 | П2-М4 | П2-М6 | П3-М1 | П3-М3 | П3-М4 | П3-М6 | П4-М2 | П4-М4 | П4-М5 |
| Суммы потенциалов | 16 | 32 | 29 | 13 | 14 | 28 | 13 | 11 | 8 | 24 | 7 | 5 | 25 | 10 | 24 |
| Значение элементов | 24 | 42 | 39 | 21 | 9 | 24 | 33 | 29 | 24 | 20 | 45 | 23 | 36 | 40 | 30 |
| Характеристики | 8 | 10 | 10 | 8 | -5 | -4 | 20 | 18 | 16 | -4 | 38 | 18 | 11 | 30 | 6 |
+П2М1 -П2М3 +П4М3 -П4М1
| Поставщики и объемы вывоза, т | Потребители и объемы завоза | Потенциалы строк | ||||||
| М1 | М2 | М3 | М4 | М5 | М6 | |||
| 92 | 84 | 80 | 112 | 96 | 36 | |||
| П1 | 144 | 24 | 30 | 42 | 15 | 39 | 21 | 0 |
| 32 | 112 | |||||||
| П2 | 148 | 9 | 24 | 30 | 33 | 27 | 29 | -2 |
| 76 | 72 | |||||||
| П3 | 76 | 24 | 22 | 20 | 45 | 21 | 23 | -8 |
| 52 | 24 | |||||||
| П4 | 132 | 11 | 36 | 27 | 40 | 30 | 8 | 0 |
| 16 | 80 | 36 | ||||||
| Потенциалы столбцов | 11 | 30 | 27 | 15 | 29 | 8 | ||
| Шифры клеток | П1-М1 | П1-М3 | П1-М5 | П1-М6 | П2-М2 | П2-М3 | П2-М4 | П2-М6 | П3-М1 | П3-М3 | П3-М4 | П3-М6 | П4-М2 | П4-М4 | П4-М5 |
| Суммы потенциалов | 11 | 27 | 29 | 8 | 28 | 25 | 13 | 6 | 3 | 19 | 7 | 0 | 30 | 15 | 29 |
| Значение элементов | 24 | 42 | 39 | 21 | 24 | 30 | 33 | 29 | 24 | 20 | 45 | 23 | 36 | 40 | 30 |
| Характеристики | 13 | 15 | 10 | 13 | -4 | 5 | 20 | 23 | 21 | 1 | 38 | 23 | 6 | 25 | 1 |
+П2М2 -П2М5 +П3М5 -П3М2
| Поставщики и объемы вывоза, т | Потребители и объемы завоза | Потенциалы строк | ||||||
| М1 | М2 | М3 | М4 | М5 | М6 | |||
| 92 | 84 | 80 | 112 | 96 | 36 | |||
| П1 | 144 | 24 | 30 | 42 | 15 | 39 | 21 | 0 |
| 32 | 112 | |||||||
| П2 | 148 | 9 | 24 | 30 | 33 | 27 | 29 | -6 |
| 76 | 52 | 20 | ||||||
| П3 | 76 | 24 | 22 | 20 | 45 | 21 | 23 | -12 |
| 76 | ||||||||
| П4 | 132 | 11 | 36 | 27 | 40 | 30 | 8 | -4 |
| 16 | 80 | 36 | ||||||
| Потенциалы столбцов | 15 | 30 | 31 | 15 | 33 | 12 | ||
| Шифры клеток | П1-М1 | П1-М3 | П1-М5 | П1-М6 | П2-М3 | П2-М4 | П2-М6 | П3-М1 | П3-М2 | П3-М3 | П3-М4 | П3-М6 | П4-М2 | П4-М4 | П4-М5 |
| Суммы потенциалов | 15 | 31 | 33 | 12 | 25 | 9 | 6 | 3 | 18 | 19 | 3 | 0 | 26 | 11 | 29 |
| Значение элементов | 24 | 42 | 39 | 21 | 30 | 33 | 29 | 24 | 22 | 20 | 45 | 23 | 36 | 40 | 30 |
| Характеристики | 9 | 11 | 6 | 9 | 5 | 24 | 23 | 21 | 4 | 1 | 42 | 23 | 10 | 29 | 1 |
Все свободные клетки имеют положительные характеристики, которые свидетельствуют о том, что дальнейшее улучшение плана невозможно и полученный план является оптимальным.
Объем работ составит: 32 * 30 + 112 * 15 + 76 * 9 + 52 * 24 + 20 * 27 + 76 * 21 + 16 * 11 + 80 * 27 + 36 * 8 = 9332 ткм.
Похожие работы
... положит в такой симплекс-таблице текущие базисные переменные равными Ai,0, а свободные - нулю, то будет получено оптимальное решение. Практика применения симплекс метода показала, что число итераций, требуемых для решения задачи линейного программирования обычно колеблется от 2m до 3m, хотя для некоторых специально построенных задач вычисления по правилам симплекс метода превращаются в прямой ...
... 0 505/103 0 792/103 669/103 500/103 Анализ Таблицы 6 позволяет сделать вывод о допустимости и оптимальности базиса XБ4=(x5, x7, x1, x2, x4)T. 3.4 Результат решения задачи планирования производства В результате решения поставленной задачи симплекс-методом получили набор производимой продукции x=(x1, x2, x3, x4, x5)=( 15145/103, 8910/103, 0, 1250/103, 3255/103), который удовлетворяет всем ...
... на t3 часов. Прибыль от реализации единицы готового изделия А составляет a рублей, а изделия В - b рублей. Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации. Решить задачу простым симплекс-методом. Дать геометрическое истолкование задачи, используя для этого её формулировку с ограничениями-неравенствами. а1 = 1 b1 = 5 t1 = 10 a = 2 а2 = 3 b2 = 2 t2 ...
... - метод для решения задач линейного программирования. Задачи курсовой заботы: 1. привести теоретический материал; 2. на примерах рассмотреть симплекс метод; 3. представить данную курсовую работу в виде презентации. Математическое программирование Математическое программирование занимается изучение экстремальных задач и поиском методов их решения. Задачи ...
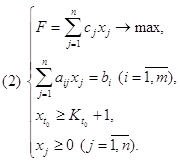

0 комментариев