Навигация
ВВЕДЕНИЕ
Цель данного курсового проекта - составить план производства требуемых изделий, обеспечивающий максимальную прибыль от их реализации, свести данную задачу к задаче линейного программирования, решить её симплекс - методом и составить программу для решения задачи этим методом на ЭВМ.
1. КРАТКИЙ ОБЗОР АЛГОРИТМОВ РЕШЕНИЯ ЗАДАЧ ДАННОГО ТИПА
1.1 Математическое программирование
Математическое программирование занимается изучение экстремальных задач и поиском методов их решения. Задачи математического программирования формулируются следующим образом : найти экстремум некоторой функции многих переменных f ( x1, x2, ... , xn ) при ограничениях gi ( x1, x2, ... , xn ) * bi , где gi - функция, описывающая ограничения, * - один из следующих знаков £ , = , ³ , а bi - действительное число, i = 1, ... , m. f называется функцией цели ( целевая функция ).
Линейное программирование - это раздел математического программирования, в котором рассматриваются методы решения экстремальных задач с линейным функционалом и линейными ограничениями, которым должны удовлетворять искомые переменные.
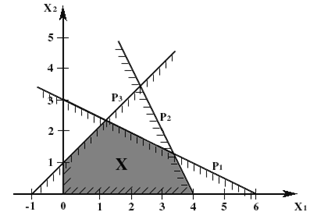
Задачу линейного программирования можно сформулировать так . Найти max
![]()
при условии : a11 x1 + a12 x2 + . . . + a1n xn £ b1 ;
a21 x1 + a22 x2 + . . . + a2n xn £ b2 ;
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
am1 x1 + am2 x2 + . . . + amn xn £ bm ;
x1 ³ 0, x2 ³ 0, . . . , xn ³ 0 .
Эти ограничения называются условиями неотрицательности. Если все ограничения заданы в виде строгих равенств, то данная форма называется канонической.
В матричной форме задачу линейного программирования записывают следующим образом. Найти max cT x
при условии
A x £ b ;
x ³ 0 ,
где А - матрица ограничений размером ( m´ n), b(m´ 1) - вектор-столбец свободных членов, x(n ´ 1) - вектор переменных, сТ = [c1, c2, ... , cn ] - вектор-строка коэффициентов целевой функции.
Решение х0 называется оптимальным, если для него выполняется условие сТ х0 ³ сТ х , для всех х Î R(x).
Поскольку min f(x) эквивалентен max [ - f(x) ] , то задачу линейного программирования всегда можно свести к эквивалентной задаче максимизации.
Для решения задач данного типа применяются методы:
1) графический;
2) табличный ( прямой, простой ) симплекс - метод;
3) метод искусственного базиса;
4) модифицированный симплекс - метод;
5) двойственный симплекс - метод.
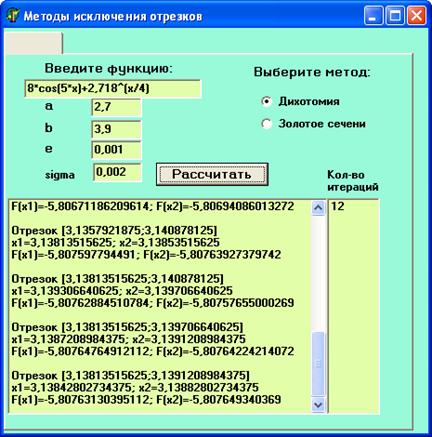
1.2 Табличный симплекс - метод
Для его применения необходимо, чтобы знаки в ограничениях были вида “ меньше либо равно ”, а компоненты вектора b - положительны.
Алгоритм решения сводится к следующему :
Приведение системы ограничений к каноническому виду путём введения дополнительных переменных для приведения неравенств к равенствам.
Если в исходной системе ограничений присутствовали знаки “ равно ” или “ больше либо равно ”, то в указанные ограничения добавляются
искусственные переменные, которые так же вводятся и в целевую функцию со знаками, определяемыми типом оптимума.
Формируется симплекс-таблица.
Рассчитываются симплекс-разности.
Принимается решение об окончании либо продолжении счёта.
При необходимости выполняются итерации.
На каждой итерации определяется вектор, вводимый в базис, и вектор, выводимый из базиса. Таблица пересчитывается по методу Жордана-Гаусса или каким-нибудь другим способом.
1.3 Метод искусственного базиса
Данный метод решения применяется при наличии в ограничении знаков “ равно ”, “ больше либо равно ”, “ меньше либо равно ” и является модификацией табличного метода. Решение системы производится путём ввода искусственных переменных со знаком, зависящим от типа оптимума, т.е. для исключения из базиса этих переменных последние вводятся в целевую функцию с большими отрицательными коэффициентами m , а в задачи минимизации - с положительными m . Таким образом из исходной получается новая m - задача.
Если в оптимальном решении m - задачи нет искусственных переменных, это решение есть оптимальное решение исходной задачи. Если же в оптимальном решении m - задачи хоть одна из искусственных переменных будет отлична от нуля, то система ограничений исходной задачи несовместна и исходная задача неразрешима.
1.4 Модифицированный симплекс - метод
В основу данной разновидности симплекс-метода положены такие особенности линейной алгебры , которые позволяют в ходе решения задачи работать с частью матрицы ограничений. Иногда метод называют методом обратной матрицы.
В процессе работы алгоритма происходит спонтанное обращение матрицы ограничений по частям, соответствующим текущим базисным векторам. Указанная способность делает весьма привлекательной машинную реализацию вычислений вследствие экономии памяти под промежуточные переменные и значительного сокращения времени счёта. Хорош для ситуаций, когда число переменных n значительно превышает число ограничений m.
В целом, метод отражает традиционные черты общего подхода к решению задач линейного программирования, включающего в себя канонизацию условий задачи, расчёт симплекс-разностей, проверку условий оптимальности, принятие решений о коррекции базиса и исключение Жордана-Гаусса.
Особенности заключаются в наличии двух таблиц - основной и вспомагательной, порядке их заполнения и некоторой специфичности расчётных формул.
Похожие работы
... - метод для решения задач линейного программирования. Задачи курсовой заботы: 1. привести теоретический материал; 2. на примерах рассмотреть симплекс метод; 3. представить данную курсовую работу в виде презентации. Математическое программирование Математическое программирование занимается изучение экстремальных задач и поиском методов их решения. Задачи ...
... ограничения несовместны, множество планов пусто и задача ЛП решения не имеет. Рис. 1.4 Рис. 1.5 Рис. 1.6 2. Симплекс-метод 2.1 Идея симплекс-метода Рассмотрим универсальный метод решения канонической задачи линейного программирования , , , с n переменными и m ограничениями-равенствами, известный как симплекс-метод. Множество планов канонической задачи – ...
... 0 505/103 0 792/103 669/103 500/103 Анализ Таблицы 6 позволяет сделать вывод о допустимости и оптимальности базиса XБ4=(x5, x7, x1, x2, x4)T. 3.4 Результат решения задачи планирования производства В результате решения поставленной задачи симплекс-методом получили набор производимой продукции x=(x1, x2, x3, x4, x5)=( 15145/103, 8910/103, 0, 1250/103, 3255/103), который удовлетворяет всем ...
... Метод преобразования целевой функции, метод штрафных функций, табличный симплекс – метод. Список используемой литературы 1. А.Г.Трифонов. Постановка задачи оптимизации и численные методы ее решения; 2. Б. Банди. Методы оптимизации. Вводный курс., 1988; 3. Мендикенов К.К. Лекции Приложение А using System; using System.Collections.Generic; using System.ComponentModel; using System. ...

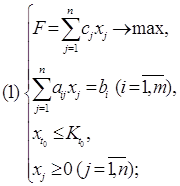
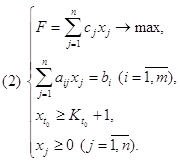
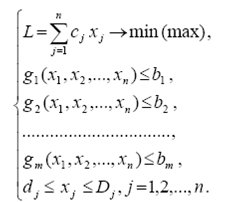
0 комментариев