Навигация
Практическое применение производственной функции
3. Практическое применение производственной функции
3.1 Моделирование издержек и прибыли предприятия (фирмы)
В основе построения моделей поведения производителя (отдельного предприятия или фирмы; объединения или отрасли) лежит представление о том, что производитель стремится к достижению такого состояния, при котором ему была бы обеспечена наибольшая прибыль при сложившихся рыночных условиях, т.е. прежде всего при имеющейся системе цен.
Наиболее простая модель оптимального поведения производителя в условиях совершенной конкуренции имеет следующий вид: пусть предприятие (фирма) производит один продукт в количестве y физических единиц. Если p экзогенно заданная цена этого продукта и фирма реализует свой выпуск полностью, то она получает валовой доход (выручку) в размере
![]()
В процессе создания этого количества продукта фирма несет производственные издержки в размере C ( y ). При этом естественно считать, что C' ( y ) > 0, т.е. издержки возрастают с увеличением объема производства. Также обычно полагают, что C'' ( y ) > 0. Это означает, что дополнительные (маргинальные) издержки на производство каждой дополнительной единицы продукции возрастают по мере увеличения объема производства. Это предположение связано с тем, что при рационально организованном производстве, при малых объемах могут быть использованы лучшие машины и высококвалифицированные работники, которых уже не окажется в распоряжении фирмы,когда объем производства вырастет. На рис. 4.10 представлены типичные графики функций R ( y ) и C ( y ). Производственные издержки состоят из следующих составных частей:
1) материальные затраты C m , в число которых входят расходы на сырье, материалы, полуфабрикаты и т.п.
Разность между валовым доходом и материальными затратами называется добавленной стоимостью (условно чистой продукцией):
![]()
2) расходы на оплату труда C L ;
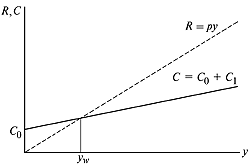
Рис. 10. Линии выручки и издержек предприятия
3) расходы, связанные с использованием, ремонтом машин и оборудования, амортизация, так называемая оплата услуг капитала C k ;
4) дополнительные расходы C r , связанные с расширением производства, строительством новых зданий, подъездных путей, линий связи и т.д.
Совокупные производственные издержки:
![]()
Как уже было отмечено выше,
![]()
однако эта зависимость от объема выпуска ( у ) для разных видов издержек различна. А именно имеют место:
а) постоянные расходы C 0 , которые практически не зависят от y , в т.ч. оплата административного персонала, аренда и содержание зданий и помещений, амортизационные отчисления, проценты за кредит, услуги связи и т.п.;
б) пропорциональные объему выпуска (линейные) затраты C 1 , сюда входят материальные затраты C m , оплата труда производственного персонала (часть C L ), расходы по содержанию действующего оборудования и машин (часть C k ) и т.п.:
![]()
где а обобщенный показатель затрат указанных видов в расчете на одно изделие;
в) сверхпропорциональные (нелинейные) затраты С 2 , в составе которых выступают приобретение новых машин и технологий (т.е. затраты типа С r ), оплата сверхурочного труда и т.п. Для математического описания этого вида затрат обычно используется степенная зависимость
![]()
Таким образом, для представления совокупных издержек можно использовать модель
![]()
(Заметим, что условия C' ( y ) > 0, C'' ( y ) > 0 для этой функции выполнены.)
Рассмотрим возможные варианты поведения предприятия (фирмы) для двух случаев:
1. Предприятие имеет достаточно большой резерв производственных мощностей и не стремится к расширению производства, поэтому можно полагать, что C 2 = 0 и совокупные издержки являются линейной функцией объема выпуска:
![]()
Прибыль составит
![]()
Очевидно, что при малых объемах выпуска
![]()
фирма несет убытки, так как П < 0.
Здесь y w точка безубыточности (порог рентабельности), определяемая соотношением
![]()
Если y > y w , то фирма получает прибыль, и окончательное решение об объеме выпуска зависит от состояния рынка сбыта производимой продукции (см. рис. 10).
2. В более общем случае, когда С 2 0, имеются две точки безубыточности ![]() и
и ![]() причем положительную прибыль фирма получит, если объем выпуска y удовлетворяет условию
причем положительную прибыль фирма получит, если объем выпуска y удовлетворяет условию
![]()
На этом отрезке в точке ![]() достигается наибольшее значение прибыли. Таким образом, существует оптимальное решение задачи о максимизации прибыли. В точке А , соответствующей издержкам при оптимальном выпуске, касательная к кривой издержек С параллельна прямой линии дохода R .
достигается наибольшее значение прибыли. Таким образом, существует оптимальное решение задачи о максимизации прибыли. В точке А , соответствующей издержкам при оптимальном выпуске, касательная к кривой издержек С параллельна прямой линии дохода R .
Следует заметить, что окончательное решение фирмы также зависит от состояния рынка, но с точки зрения соблюдения экономических интересов ей следует рекомендовать оптимизирующее значение выпуска (рис. 11).
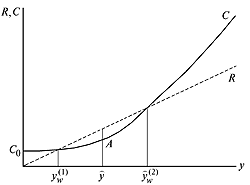
Рис. 11. Оптимальный объем выпуска
В общем случае, когда С ( у ) является нелинейной возрастающей и выпуклой вниз функцией (так как С' ( у ) > 0 и С'' ( у ) > 0) объема выпуска, ситуация полностью аналогична той, которая рассмотрена в пункте 2. По определению прибылью считается величина
![]()
Точки безубыточности ![]() и
и ![]() определяются из условия равенства прибыли нулю, а максимальное ее значение достигается в точке
определяются из условия равенства прибыли нулю, а максимальное ее значение достигается в точке ![]() которая удовлетворяет уравнению
которая удовлетворяет уравнению
![]() или
или ![]()
Таким образом, оптимальный объем производства характеризуется тем, что в этом состоянии маргинальный валовой доход ( R ( y )) в точности равен маргинальным издержкам C ( y ).
В самом деле, если y < ![]() то R ( y ) > C ( y ), и тогда следует увеличить выпуск продукции, поскольку ожидаемый дополнительный доход превысит ожидаемые дополнительные издержки. Если же y >
то R ( y ) > C ( y ), и тогда следует увеличить выпуск продукции, поскольку ожидаемый дополнительный доход превысит ожидаемые дополнительные издержки. Если же y > ![]() то R ( y ) < C ( y ), и всякое увеличение объема уменьшит прибыль, поэтому естественно рекомендовать уменьшить объем производства и придти в состояние y =
то R ( y ) < C ( y ), и всякое увеличение объема уменьшит прибыль, поэтому естественно рекомендовать уменьшить объем производства и придти в состояние y = ![]() (рис. 12).
(рис. 12).
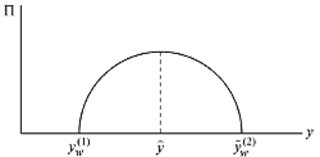
Рис. 12. Точка максимума прибылии зона безубыточности
|
| (*) |
Нетрудно видеть, что при увеличении цены ( р ) оптимальный выпуск, а также прибыль увеличиваются, т.е.
![]()
Это верно также и в общем случае, так как
![]()
Пример. Фирма производит сельскохозяйственные машины в количестве у штук, причем объем производства в принципе может изменяться от 50 до 220 штук в месяц. При этом естественно увеличение объема производства потребует увеличения затрат как пропорциональных, так и сверхпропорциональных (нелинейных), поскольку потребуется приобрести новое оборудование и расширить производственные площади.
В конкретном примере будем исходить из того, что общие издержки (себестоимость) на производство продукции в количестве у изделий выражаются формулой
C ( y ) = 1000 + 20 y + 0,1 y 2 (тыс. руб.).
Это означает, что постоянные издержки
C 0 = 1000 (т. руб.),
пропорциональные затраты
C 1 = 20 y ,
т.е. обобщенный показатель этих затрат в расчете на одно изделие равен: а = 20 тыс. руб., а нелинейные затраты составят C 2 = 0,1 y 2 ( b = 0,1).
Приведенная выше формула для издержек является частным случаем общей формулы, где показатель h = 2.
Для нахождения оптимального объема производства воспользуемся формулой точки максимума прибыли (*), согласно которой имеем:
![]()
Совершенно очевидно, что объем производства, при котором достигается максимальная прибыль, весьма существенно определяется рыночной ценой изделия p .
В табл. 1 представлены результаты расчета оптимальных объемов при различных значениях цены от 40 до 60 тыс. рублей за изделие.
В первом столбце таблицы фигурируют возможные объемы выпуска у , второй столбец содержит данные о полных издержках С ( у ), в третьем столбце представлена себестоимость в расчете на одно изделие:

Таблица 1
Данные об объемах выпуска, затратах и прибыли
| Объемы и затраты | Цены и прибыли | ||||||||
| Y | C | AC | MC | 40 | 42 | 44 | 50 | 54 | 60 |
| 50 | 2250 | 45 | 30 | - 250 | - 150 | - 50 | 250 | 450 | 740 |
| 33 | |||||||||
| 80 | 3240 | 40,5 | 36 | -40 | +120 | 280 | 760 | 1080 | 1560 |
| 38 | |||||||||
| 100 | 4000 | 40 | 40 | 0 | 200 | 400 | 1000 | 1400 | 2000 |
| 41 | |||||||||
| 110 | 4410 | 40,1 | 42 | - 10 | 210 | 430 | 1090 | 1530 | 2190 |
| 43 | |||||||||
| 120 | 4840 | 40,3 | 44 | - 40 | 200 | 440 | 1160 | 1640 | 2360 |
| 47 | |||||||||
| Продолжение таблицы 1 | |||||||||
| 150 | 6250 | 41,7 | 50 | - 250 | 50 | 350 | 1250 | 1850 | 2750 |
| 52 | |||||||||
| 170 | 7290 | 42,9 | 54 | - 490 | - 150 | 190 | 1210 | 1890 | 2910 |
| 57 | |||||||||
| 200 | 9000 | 45 | 60 | - 1000 | - 600 | - 200 | 1000 | 1800 | 3000 |
| 62 | |||||||||
| 220 | 10240 | 46,5 | 64 | - 1440 | - 1000 | - 560 | 760 | 1640 | 2960 |
Четвертый столбец характеризует значения указанных выше маргинальных издержек МС , которые показывают, во сколько обходится производство одного дополнительного изделия в данной ситуации. Нетрудно заметить, что маргинальные издержки возрастают по мере роста производства, что хорошо согласуется с положением, высказанным в начале этого параграфа. При рассмотрении таблицы следует обратить внимание на то, что оптимальные объемы находятся точно на пересечении строки (маргинальные издержки МС) и столбца (цена p) с равными их значениями, что совершенно аккуратно соотносится с правилом оптимальности, установленным выше.
Проведенный выше анализ относится к обстановке совершенной конкуренции, когда производитель не может повлиять своими действиями на систему цен, и поэтому цена p на товар y выступает в модели производителя как экзогенная величина.
В случае же несовершенной конкуренции производитель может оказывать непосредственное влияние на цену. В особенности это относится к монопольному производителю товара, который формирует цену из соображения разумной рентабельности.
Рассмотрим фирму с линейной функцией издержек, которая определяет цену таким образом, чтобы прибыль составляла определенный процент (долю 0 < g < 1) от валового дохода, т.е.
![]()
Отсюда имеем
![]()
Валовой доход
![]()
и производство оказывается безубыточным, начиная с самых малых объемов производства ( y w 0). Легко видеть, что цена зависит от объема, т.е. p = p ( y ), и при увеличении объема производства ( у ) цена товара уменьшается, т.е. p' ( y ) < 0. Это положение имеет место для монополиста и в общем случае.
Требование максимизации прибыли для монополиста имеет вид
![]()
Предполагая по-прежнему, что ![]()
![]() имеем уравнение для нахождения оптимального выпуска (
имеем уравнение для нахождения оптимального выпуска ( ![]() ):
):
![]()
Полезно заметить, что оптимальный выпуск монополиста (![]() ) как правило, не превосходит оптимального выпуска конкурентного производителя
) как правило, не превосходит оптимального выпуска конкурентного производителя ![]() в формуле, помеченной звездочкой (С.37).
в формуле, помеченной звездочкой (С.37).
Более реалистичная (но также простая) модель фирмы используется для того, чтобы учесть ресурсные ограничения, которые играют очень большую роль в хозяйственной деятельности производителей. В модели выделяется один наиболее дефицитный ресурс (рабочая сила, основные фонды, редкий материал, энергия и т.п.) и предполагается, что фирма может его использовать не более чем в количестве Q . Фирма может производить n различных продуктов. Пусть y 1 , ..., y j , ..., y n искомые объемы производства этих продуктов; p 1 , ..., p j , ..., p n их цены. Пусть также q цена единицы дефицитного ресурса. Тогда валовой доход фирмы равен
![]()
а прибыль составит
![]()
Легко видеть, что при фиксированных q и Q задача о максимизации прибыли преобразуется в задачу максимизации валового дохода.
Предположим далее, что функция издержек ресурса для каждого продукта C j ( y j ) обладает теми же свойствами, которые были высказаны выше для функции С ( у ). Таким образом, C j ' ( y j ) > 0 и C j '' ( y j ) > 0.
В окончательном виде модель оптимального поведения фирмы с одним ограниченным ресурсом следующая:
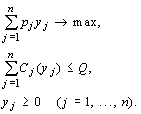
Нетрудно видеть, что в достаточно общем случае решение этой оптимизационной задачи находится путем исследования системы уравнений:
|
| (**) |
Где j множитель Лагранжа.
Заметим, что соотношение
![]()
является по существу аналогом отмеченного выше совпадения в оптимальной точке маргинального дохода и маргинальных издержек. В случае квадратичных функций издержек
![]()
из системы уравнений (**) имеем:
|
| (***) |
Заметим, что оптимальный выбор фирмы зависит от всей совокупности цен на продукты ( p 1 , ..., p n ), причем этот выбор является однородной функцией системы цен, т.е. при одновременном изменении цен в одинаковое число раз оптимальные выпуски ![]() не изменяются. Нетрудно видеть также, что из уравнений, помеченных звездочками (***), следует, что при увеличении цены на продукт n (при неизменных ценах на другие продукты) его выпуск следует увеличить с целью получения максимальной прибыли, так как
не изменяются. Нетрудно видеть также, что из уравнений, помеченных звездочками (***), следует, что при увеличении цены на продукт n (при неизменных ценах на другие продукты) его выпуск следует увеличить с целью получения максимальной прибыли, так как
![]()
а производство остальных товаров уменьшится, так как
![]()
Эти соотношения в совокупности показывают, что в данной модели все продукты являются конкурирующими. Из формулы (***) вытекает также очевидное соотношение
![]()
т.е. при увеличении объема ресурса (капиталовложений, рабочей силы и т.п.) оптимальные выпуски увеличиваются.
Можно привести ряд простых примеров, которые помогут лучше понять правило оптимального выбора фирмы по принципу максимума прибыли:
1) пусть n = 2; p 1 = p 2 = 1; a 1 = a 2 = 1; Q = 0,5; q = 0,5.
Тогда из (***) имеем:
![]() = 0,5;
= 0,5; ![]() = 0,5; П = 0,75;
= 0,5; П = 0,75; ![]() = 1;
= 1;
2) пусть теперь все условия остались прежними, но удвоилась цена на первый продукт: p 1 = 2.
Тогда оптимальный по прибыли план фирмы: ![]() = 0,6325;
= 0,6325; ![]() = 0,3162.
= 0,3162.
Ожидаемая максимальная прибыль заметно возрастает: П = 1,3312; ![]() = 1,58;
= 1,58;
3) заметим, что в предыдущем примере 2 фирма должна изменить объемы производств, увеличив производство первого и уменьшив производство второго продукта. Предположим, однако, что фирма не гонится за максимальной прибылью и не станет менять налаженное производство, т.е. выберет программу y 1 = 0,5; y 2 = 0,5.
Оказывается, что в этом случае прибыль составит П = 1,25. Это означает, что при повышении цен на рынке фирма может получить значительное увеличение прибыли без изменения плана выпуска.
Похожие работы
... времени. Возможно, что владение социальной квалификацией, highsos, станет в будущем даже важнее, чем владение техникой, hightech. 2. Метод социометрических измерений. Сущность и область применения. Успешность решения проблемы измерения является одной из главных компонент, составляющих понятие качества социологического исследования. Однако далеко не каждый социолог об этом задумывается. ...
... рождения экономической науки (1750-1870 гг.), этап открытия и разработки основополагающих теоретических принципов (1870-1930 гг.) и этап современного углубления и расширения исследований. 1-й этап. Корни политэкономии лежат, с одной стороны, в философии, а с другой – в спорах о насущных проблемах и трудностях (Аристотель, Платон, стоики, эпикурейцы). Начиная с Возрождения и Реформации наступает ...
... самоопределении, целевом и ценностном проектировании заложены основы гибкости деятельности и достижения адекватности человека как социально организуемой деятельности, так и своим потребностям, целям, ценностям, идеалам. Средством реализации комплекса обозначенных характеристик обучения являются активные методы обучения. Особенностью этих методов является то, что их реализация возможна лишь через ...
... познавательной деятельности происходит в результате (путем) личностной и групповой рефлексии на всех этапах работы над проектом. [15, 39-46] 1.4 Психолого-педагогические основания применения метода проектов в экологическом воспитании детей младшего школьного возраста Личностный подход к процессу обучения и воспитания младших школьников позволял изучать окружающую среду, «вмешиваться в ...
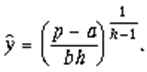
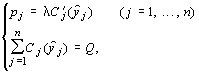
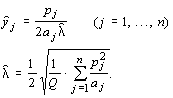
0 комментариев