Навигация
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
кафедра РЭС
реферат на тему:
«Линейные блоковые коды»
МИНСК, 2009
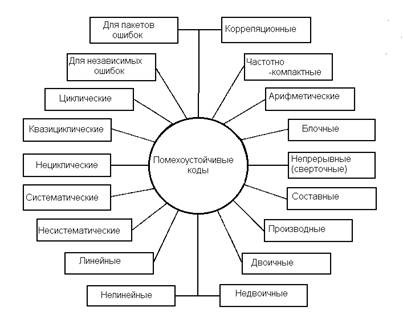
Линейным блоковым (n,k) - кодом называется множество N последовательностей длины n над GF(q), называемых кодовыми словами, которое характеризуется тем, что сумма двух кодовых слов является кодовым словом, а произведение любого кодового слова на элемент поля также является кодовым словом.
Обычно N=qk , где k - некоторое целое число. Если q=2, линейные коды называются групповыми, так как кодовые слова образуют математическую структуру, называемую группой. При формирование этого кода линейной операцией является суммирование по mod2.
Способы задания линейных кодов1. Перечислением кодовых слов, т.е. составлении списка всех кодовых слов кода.
Пример. В таблице 1 представлены все кодовые слова (5,3) - кода (ai - информационные, а bi - проверочные символы).
| Таблица 1 | |||||
| № | a1 | a2 | a3 | b1 | b2 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 2 | 0 | 1 | 0 | 1 | 1 |
| 3 | 0 | 1 | 1 | 0 | 1 |
| 4 | 1 | 0 | 0 | 0 | 1 |
| 5 | 1 | 0 | 1 | 1 | 1 |
| 6 | 1 | 1 | 0 | 1 | 0 |
| 7 | 1 | 1 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 0 | 0 |
2. Системой проверочных уравнений, определяющих правила формирования проверочных символов по известным информационным:
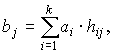
где
j - номер проверочного символа;
i - номер информационного символа;
hij - коэффициенты, принимающие значения 0 или 1 в соответствии с правилами формирования конкретных групповых кодов.
Пример. Для кода (5,3) проверочные уравнения имеют вид:
b1= a2 + a3;
b2= a1 + a2.
3. Матричное, основанное на построении порождающей и проверочной матриц.
Векторное пространство Vn над GF(2) включает в себя 2n векторов (n-последовательностей), а подпространством его является множество из 2k кодовых слов длины n, которое однозначно определяется его базисом, состоящим из k линейно независимых векторов. Поэтому линейный (n,k) - код полностью определяется набором из k кодовых слов, принадлежащих этому коду. Набор из k кодовых слов, соответствующих базису, обычно представляется в виде матрицы, которая называется порождающей.
Пример. (5,3) - код, который был представлен в таблице 1, может быть задан матрицей
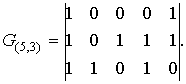
Остальные кодовые слова получаются сложением строк матриц в различных сочетаниях.
Общее количество различных вариантов порождающих матрицу определяется выражением
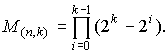
Для исключения неоднозначности в записи G(n,k) вводят понятие о канонической или систематической форме матрицы, которая имеет вид
![]()
где
Ik - единичная матрица, содержащая информационные символы;
Rk,r - прямоугольная матрица, составленная из проверочных символов.
Пример. Порождающая матрица в систематическом виде для (5,3) - кода
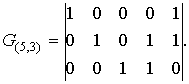
Порождающая матрица G(n,k) в систематическом виде может быть получена из любой другой матрицы посредством элементарных операций над строками (перестановкой двух произвольных строк, заменой произвольной строки на сумму ее самой и ряда других) и дальнейшей перестановкой столбцов.
Проверочная матрица в систематическом виде имеет вид
![]()
где Ir - единичная матрица;![]() - прямоугольная матрица в транспонированном виде матрицы Rk,r из порождающей матрицы.
- прямоугольная матрица в транспонированном виде матрицы Rk,r из порождающей матрицы.
Пример. Проверочная матрица (5,3) - кода
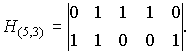
Основные свойства линейных кодов
1. Произведение любого кодового слова![]() на транспонированную проверочную матрицу дает нулевой вектор размерности (n-k)
на транспонированную проверочную матрицу дает нулевой вектор размерности (n-k)
![]()
Пример. для кода (5,3)
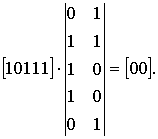
2. Произведение некоторого кодового слова![]() , т.е. с ошибкой, на транспонированную проверочную матрицу называется синдромом и обозначается Si(x)
, т.е. с ошибкой, на транспонированную проверочную матрицу называется синдромом и обозначается Si(x)
![]()
3. Между порождающей и проверочной матрицами в систематическом виде существует однозначное соответствие, а именно:
![]()
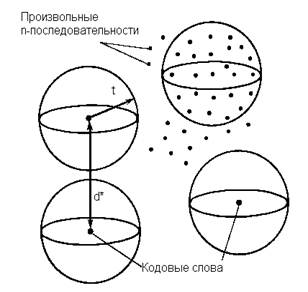
4. Кодовое расстояние d0 (n,k) - кода равно минимальному числу линейно зависимых столбцов проверочной матрицы
Пример.
для кода (5,3):
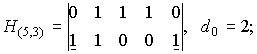
для кода (5,2):
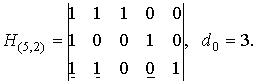
Похожие работы
... процедуру перемешивания порядка символов в закодированной последовательности перед передачей и восстановлением исходного порядка символов после приема с тем, чтобы рандомизировать ошибки, объединенные в пакеты. Особенности практического кодирования Предположим, что все представляющие интерес данные могут быть представлены в виде двоичной (закодированной двоично) информации, т. е. в виде ...
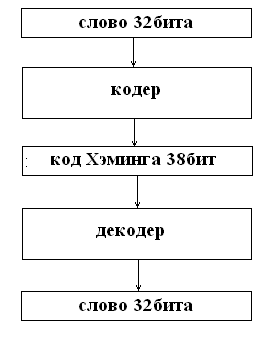
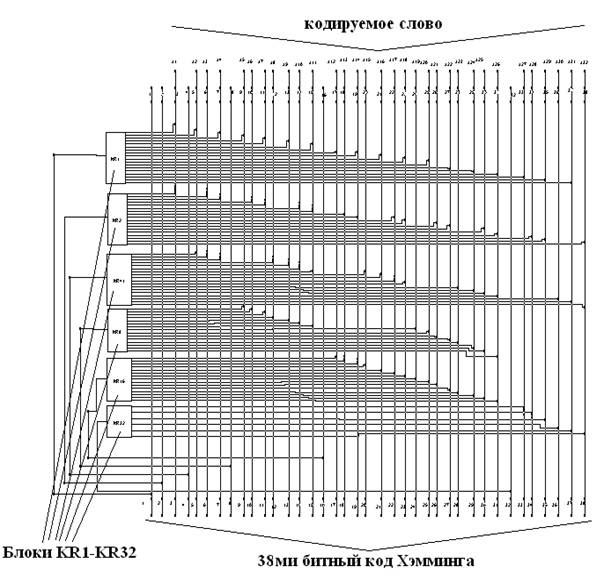
... кодирования можно разработать устройство, которое поможет понять принцип работы метода Хэмминга. Кодер – декодер будем разрабатывать на основе ИМС К555ВЖ1. 2.1 Разработка устройства кодирования информации методом Хемминга Кодер, преобразует 32х битное слово в 38ми разрядный код Хэмминга, после чего слово хранится в памяти или передаётся по шинам и т.д. В процессе передачи или хранения в ...
... время является технология ADSL (Asymmetric Digital Subscriber Line). Это новая модемная технология, превращающая стандартные абонентские телефонные аналоговые линии в линии высокоскоростного доступа. Технология ADSL позволяет передавать информацию к абоненту со скоростью до 8 Мбит/с. В обратном направлении используется скорость до 640 Кбит/с. Это связанно с тем, что все современный спектр сетевых ...
дства разработки алгоритмов кодирования источника, помехоустойчивого кодирования, перемежения, модуляции, демодуляция и эквализации. Генерация проверочной и порождающей матриц для кода Хэмминга Синтаксис: h = hammgen(m); h = hammgen(m,pol); [h,g] = hammgen(...); [h,g,n,k] = hammgen(...); Описание: Для всех вариантов синтаксиса длина кодового слова обозначается как n. Величина n ...
0 комментариев