Лабораторная работа
Метод конечных разностей
Цель работы
Ознакомиться с аналоговым и дискретным вариантами реализации фильтра
Общие сведения
Если известны значения некоторой функции ![]() для равноотстоящих значений аргумента
для равноотстоящих значений аргумента
![]() ,
,
где ![]() .
.
Здесь
![]()
Тогда можно говорить, что задана таблица функции ![]() с шагом
с шагом ![]() , начальным значением аргумента
, начальным значением аргумента ![]() и конечным значением аргумента
и конечным значением аргумента ![]() .
.
Конечными разностями первого порядка функции ![]() называются числа
называются числа
![]()
Аналогично определяются конечные разности второго порядка
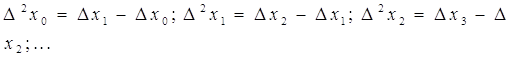
Тогда разности ![]() порядка определяются соотношениями
порядка определяются соотношениями
![]()
Таблица значений функции и её конечных разностей
| y | x |
|
|
|
|
|
|
| ||||
|
| |||||
|
|
|
| |||
|
|
| ||||
|
|
|
|
| ||
|
|
| ||||
|
|
|
|
| ||
|
|
| ||||
|
|
|
| |||
|
| |||||
|
|
|
Таким образом, все разности чётного порядка располагаются в тех же (горизонтальных) строчках, что и аргументы, все нечётные разности располагаются в промежуточных строчках.
При программной реализации воспользуемся методом четвёртых разностей
Представим график исследуемой функции в следующем виде
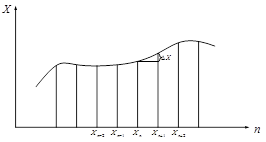
Разность первого порядка здесь будет определяться следующим выражением:
![]()
Разность второго порядка с учётом предыдущего выражения примет вид:
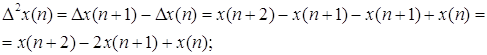
Аналогично определяются разности третьего и четвёртого порядков. Выполнив подстановку и приведение подобных получим следующие выражения:
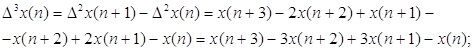
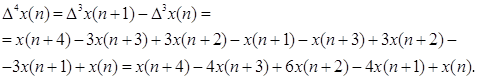
В обобщённом виде рекуррентное соотношение для вычисления сглаженного значения полезного сигнала в очередном i-том цикле расчёта:
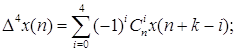
где
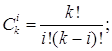
Похожие работы
... . Одним из наиболее универсальных и эффективных методов, получивших в настоящее время широкое распространение для приближённого решения уравнений математической физики, является метод конечных разностей или метод сеток. Суть метода состоит в следующем. Область непрерывного изменения аргументов, заменяется дискретным множеством точек (узлов), которое называется сеткой или решёткой. Вместо функции ...
... что , последнее выражение дает возможность после раскрытия скобок выделить из суммы и оценить сначала абсолютную погрешность, а по абсолютной погрешности – относительную: Условные арифметические операторы с проверкой равенства операндов необходимо заменять проверкой вида: .2. Конечные разности 2.1 Определение конечных разностей Конечная разность «вперед» для таблично заданной функции ...
... - - - 0 - - - 1 - - - В таблице жирным шрифтом выделены конечные разности от нулевого порядка и выше, которые входят в интерполяционную формулу Ньютона. 4.2 Рекуррентные формулы Адамса Пусть теперь требуется найти решение уравнения . для которого уже каким-либо способом найдены k+1 значений решения , что, естественно, определяет и ...
... с помощью рекурентных соотношений? 104) Приведите конечно-разностные выражения для первой производной. 105) Подынтегральная функция y = f(x) задана таблицейВзяв h = 0,3, вычислить интеграл на отрезке [0,3; 0,9] методом Симпсона. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету ЧИСЛЕННЫЕ МЕТОДЫ Билет № 22 106) Как ...
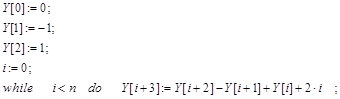
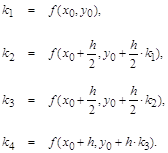
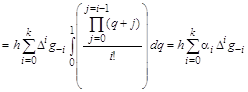
0 комментариев