Формула Планка. Виведення законів Стефана-Больцмана й Віна

4. Формула Планка. Виведення законів Стефана-Больцмана й Віна

 

Значення спектральної випромінювальної здатності абсолютно чорного тіла було знайдено німецьким фізиком М. Планком у 1900 р. Для цього йому довелося відмовитися від одного із основних положень класичної фізики, відповідно до якого енергія будь-якої випромінювальної системи може змінюватися неперервно, тобто приймати довільні –значення. Відповідно до висунутої Планком квантової гіпотези, атомні осцилятори випромінюють енергію не безупинно, а певними порціями – квантами, причому енергія кванта пропорційна частоті коливання:

 (12)

де  – стала Планка.

Так як енергія випромінювання випускається порціями, то енергія осцилятора ε може приймати лише певні дискретні значення, кратні цілому числу елементарних порцій енергії ε₀:

 (n= 0,1,2,…)

Використовуючи статистичні методи й квантовий характер теплового випромінювання, М. Планк вивів формулу універсальної функції Кірхгофа

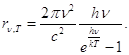 (13)

яка блискуче погоджується з експериментальними даними розподілу енергії в спектрах випромінювання абсолютно чорного тіла у всьому інтервалі частот від 0 до ∞ і при різних температурах. Теоретичний зміст цієї формули М. Планк розповів 14 грудня 1900 р. на засіданні Німецького фізичного гуртка. Цей день став датою народження квантової фізики.

Використовуючи формулу Планка можна одержати закон Стефана — Больцмана. Згідно (9)

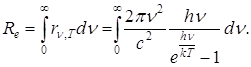
Введемо позначення х = hv/(kТ), звідки   Тут k- стала Больцмана, яка дорівнює 1,38^.10^-23 Дж/К. З урахуванням цих позначень інтегральна випромінювальна здатність абсолютно чорного тіла R_e, буде дорівнювати

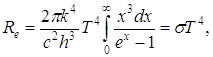 (14)

де 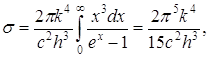 так як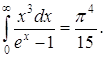

Таким чином, дійсно формула Планка дозволяє одержати закон Стефана – Больцмана. Крім того, підстановка числових значень k, с и h дає для постійної Стефана – Больцмана величину, яка добре погоджується з експериментальними даними.

Закон зміщення Віна одержимо за допомогою формули (3) і (13):

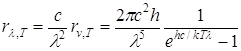. (15)

Досліджуємо вираз (15) на максимум, здійснивши попередньо такі заміни:

, звідки .

Підставимо ці заміни в (15), одержимо

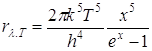. (16)

Похідну від (16) прирівняємо до нуля 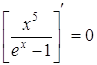, одержимо

,

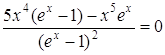звідки

 або

Розв’язавши останнє трансцендентне рівняння графічним способом рис.3, знайдемо значення змінної величини x, при якій функція (16) досягає максимуму x=4965.

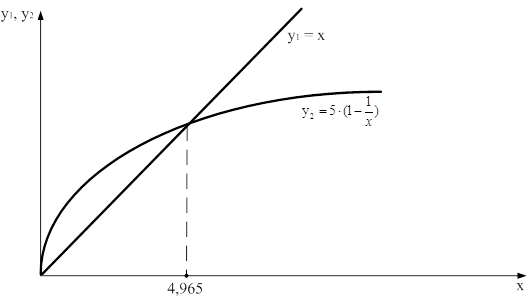
Рис. 3

Отже,

звідки

,

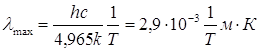тобто, ми одержали закон зміщення Віна.

Таким чином, формула Планка не тільки добре погоджується з експериментальними даними, але й містить у собі дослідні закони теплового випромінювання, а також дозволяє обчислити постійні в законах теплового випромінювання. Отже, формула Планка є повним розв’язком основного завдання теплового випромінювання, поставленого Кірхгофом. Його розв’язування стало можливим лише завдяки революційній квантовій гіпотезі Планка.

5. Зовнішній фотоефект. Ефект Комптона

Метал це тверде тіло, в якому є вільні електрони, що можуть хаотично рухатися між вузлами кристалічної решітки. Характерною особливістю металів є їх блиск. Якщо метал опромінювати світлом, то з нього вилітають вільні електрони. Цей експериментальний факт називається фотоефектом рис.4.

Рис. 4

Щоб пояснити, чому з металу вилітають електрони під дією світла, слід спочатку зрозуміти, чому вони самочинно не вилітають з металу, без дії світла, якщо вони там є.

Що таке метал? Метал - це речовина, у якій при утворенні решітки частина валентних електронів починає перебувати у вільному стані, а вузли кристалічної решітки, які втратили валентні електрони, стають позитивними іонами. Чому електрони не вилітають за межі металу, адже в ньому ніяких стінок немає? Відповідь проста: як тільки окремий електрон випадково вилітає за межі металу, то весь його шматок (до цього він був нейтральним) стає позитивно зарядженим, і утворене електричне поле цього шматка затягує електрон назад в метал.

Щоб зрозуміти цей процес дещо глибше розглянемо поведінку окремих молекул в рідині рис.5.

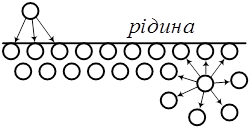
Рис.5

У рідині молекули нейтральні, а тому між ними діють молекулярні сили взаємодії. Коли молекула рідини випадково вилітає за межі її поверхні, то в більшості випадків появляються сили, які затягують її назад в рідину. З цієї причини поверхня рідини має чітку границю між стінками, а також повітряним шаром біля її поверхні.

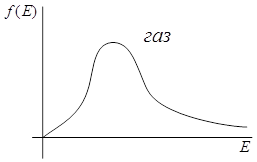
Рис.6

На рис. 6 показана залежність функції розподілу молекул повітря за кінетичними енергіями. Подібний розподіл за кінетичними енергіями характерний також для молекул рідини. Виходить у рідинах завжди є молекули, які за рахунок хаотичного теплового руху можуть мати більшу енергією, ніж потрібно для подолання роботи виходу. Такі молекули легко долають сили притягання, тобто виконують роботу по подоланню молекулярних сил притягання й вилітають за межі рідини. Цей процес називається випаровуванням.

Повернемося тепер до питання, чому самочинно не вилітають електрони з металу, адже вони в металі ведуть себе як ідеальний газ? Серед великої кількості вільних електронів у металі завжди знайдуться досить енергійні електрони, які здатні долати потенціальний бар’єр і вилітати за межі металу. За цією логікою має відбуватися безперервне випаровування електронів з металу. До чого це призвело б? Це призвело б до того, що шматок металу постійно набував би позитивного заряду. На будь-який шматок металу налипав би всякий дріб'язок, пил, папірці. Цього на практиці не спостерігається. Це означає, що електрони не випарову-ються і що функція розподілу електронів за енергіями усередині металів не така, як для газів або рідин. Дослідження залежності функції розподілу електронів за енергіями в металі показують, що вона така, як на рис.7. Був би «хвіст» у цієї функції розподілу, – електрони б випаровувалися, і шматок був би обліплений всяким дріб’язком. Максимальні енергії електронів в металі не перевищують деякого значення , а тому електрони в металі мають енергію в інтервалі . Якщо взяти інтервал енергії , то заштрихована площа дасть число електронів з енергією в цьому інтервалі, а електронів, енергії яких більші за , там немає взагалі.

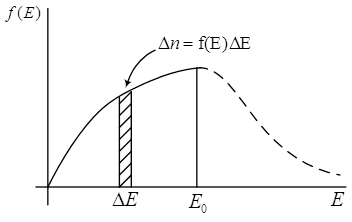
Рис.7

Факт, що метал не обліплений пилом, беззаперечно підтверджує, що функція розподілу електронів у металі немає хвоста, однак стверджувати, що енергія електронів в металі повинна мати обрив при значеннях  теж не можна.

На рис. 8 показана картина потенціальної енергії електронів у металі. Поза металом діє сила , яка затягує електрони в метал. Всередині металу електрон знову вільний, сила на нього не діє, а потенціальна енергія постійна.

Повна енергія електрона складається з потенціальної і кінетичної енергій. Енергія , на якій обривається функція розподілу, це максимальна повна енергія електрона в металі. Мінімальна повна енергія електрона близька до нуля. Весь спектр енергій електронів лежить у межах від дна цієї ями до рівня . Повна енергія електрона значно менша тієї, яку слід надати електрону, щоб він став вільним. Рівень Е – це енергія для вільного електрона. Найенергійнішому електрону (який має максимальну кінетичну енергію) усередині металу, щоб досягти до краю ями, не вистачає шматка , ця енергія називається роботою виходу.

 

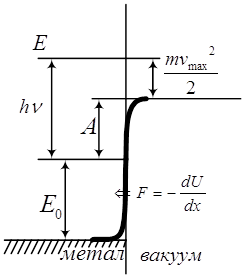
Рис.8

Чому вилітають електрони з металу під дією світла? Нічого дивного тут немає. Світло це електромагнітна хвиля, яка здатна проникати в метал, Змінне електричне поле електромагнітної хвилі може надавати електрону достатню енергію. Якщо імпульс електрона виявиться направленим до границі металу з вакуумом, то він вилетить за межі металу. Варто було б очікувати, що чим більша інтенсивність падаючого світла, тобто чим більша амплітуда хвилі, тим з більшими швидкостями будуть вилітати електрони з металу, тому що тим більшу енергію вони можуть одержати від цієї хвилі. І тут виникла перша проблема - насправді, не впливає інтенсивність світла на швидкості, з якими вилітають електрони з металу. Швидкість електрона, який вилітає за межі металу, залежить не від падаючої енергії, а від кольору. Якщо на метал направити синє світло, то електрони будуть вилітати з більшими швидкостями ніж, якщо світити червоним. Якщо світити світлом із ще більшою довжиною хвилі, то вони взагалі не будуть вилітати, яка б не була їх інтенсивність. Пояснити ці протиріччя було не так просто.

Для розв’язування цієї проблеми довелося відмовитися від хвильової теорії й визнати, що при взаємодії з речовиною світло поводиться як потік частинок, тобто повернутися до старих корпускулярних понять, які в свій час запропонував Ньютон.

Чим же відрізняються хвилі й частинки? Освітлюємо шматок металу джерелом монохроматичного світла з певною довжиною хвилі, наприклад зеленим. Вимірюємо швидкості, з якими вилітають електрони з металу. Виявляється, ці швидкості змінюються в межах від нуля до деякої максимальної швидкості. В цьому випадку не складно порахувати скільки електронів вилітає за одну секунду з металу. Коли віддалятися від джерела, інтенсивність падаючого світла знижується, але швидкості, з якими вилітають електрони, не залежить від відстані, а ось число електронів, які вилітають, залежить.

Енергія фотона пов'язана із частотою. Те, що ми у хвильовій теорії називали частотою, а просто візуально це проявляється у кольорі, визначає енергію фотона: , де h – постійна Планка. Імпульс фотона – це енергія, поділена на швидкість світла: .

Фотон – це частинка, для якої маса дорівнює нулю, і для фотона . В одних фізичних явищах світло проявляє хвильові властивості (дифракція, інтерференція), в інших корпускулярні властивості (наприклад, фотоефект).

Якщо в метал проникає фотон, який має енергію  більшу, ніж робота виходу, то електрон вилетить із металу, і надлишок енергії піде на його кінетичну енергію, і ми тоді бачимо, що

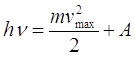. (17)

Це знаменита формула Ейнштейна. Ейнштейн у 1921 році одержав Нобелівську премію не за теорію відносності, а от за цю формулу, яку тепер може написати будь-який школяр. Здавалося б за що премія? А за те, що треба було усвідомити, що світло може проявляти квантові властивості.

Видно, що якщо енергія фотона менша роботи виходу, електрон її поглинув, підскочив і однаково з ями не вилетів, тут фотоефект не відбувається. Якщо метал освітлювати світлом із частотами меншими, ніж , то при таких частотах фотоефект взагалі не відбувається.

Мінімальна частота світлових променів, при якій ще можливий фотоефект, називається червоною межею фотоефекту.

Куди діваються фотони, якщо вони вибивають електрони з металу? Фотони поглинаються іншими атомами і зникають.

Куди подівся електрони, коли його вибивають фотони? Коли якась кількість електронів під дією світла вилетіла за межі металу, то метал набуде позитивного заряду, і, зрештою, цей заряд стане настільки великим, що максимальної кінетичної енергії, з якою вилітає електрон, не вистачить, щоб летіти в безмежність. Що тоді буде відбуватися? Електрони вилітають за межі металу і тут же повертаються назад. Це означає, що всякий шматок металу при освітленні повинен мати деякий позитивний заряд, і що він оточений хмаркою електронів біля його поверхні.

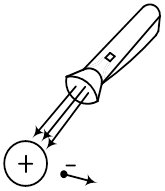
Рис.9

Розрізняють фотоефект зовнішній, внутрішній і вентильний. Зовнішнім фотоелектричним ефектом (фотоефектом) називається випромінювання електронів речовиною під дією електромагнітного випромінювання. Зовнішній фотоефект спостерігається у твердих тілах (металах, напівпровідниках, діелектриках), а також у газах на окремих атомах і молекулах (фотоіонізація).

Перші фундаментальні дослідження фотоефекту були виконані російським ученим А. Г. Столетовим. Принципова схема для дослідження фотоефекту наведена на рис. 10. Два електроди (катод К з досліджуваного металу й анод А – у схемі Столетова застосовувалася металева сітка) у вакуумній трубці ввімкнені до батареї так, що за допомогою потенціометра R можна змінювати не тільки значення, але й знак поданої на них напруги. Струм, який виникає при освітленні катода монохроматичним світлом (через кварцове віконце), вимірювався ввімкненим у ланцюг міліамперметром. Опромінюючи катод світлом різних довжин хвиль, Столетов установив наступні закономірності, які не втратили свого значення до нашого часу:

·            найбільш ефективну дію здійснюють ультрафіолетові промені;

·            під дією світла речовина втрачає тільки негативні заряди;

·            сила струму, яка виникає під дією світла, прямо пропорційна його інтенсивності.

У 1899 р. фізики Ф. Ленард і У. Томсон методом відхилення зарядів у електричному й магнітному полях визначили питомий заряд частинок, які вириваються світлом з катода, довівши, що ці частинки є електронами (рис. 10).

Це було підтверджено в 1922 р. дослідами А.Ф. Йоффе й Н.И. Добронравова, які досліджували фотоефект на мікроскопічних заряджених металевих порошинах.

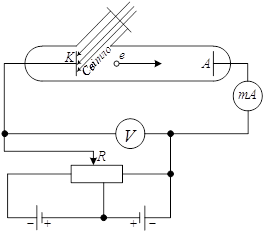
Рис.10

Внутрішній фотоефект - це викликані електромагнітним випромінюванням переходи електронів усередині напівпровідника або діелектрика із зв'язаних станів у вільні стани без вильоту назовні. У результаті концентрація носіїв струму усередині тіла збільшується, що приводить до виникнення фотопровідності (підвищенню електропровідності напівпровідника або діелектрика при його освітленні) або до виникнення е.р.с.

Вентильний фотоефект - виникнення е.р.с. при освітленні контакту двох різних напівпровідників або напівпровідника й металу (при відсутності зовнішнього електричного поля). Вентильний фотоефект відкриває, таким чином, шляхи для прямого перетворення сонячної енергії в електричну.

6. Ефект Компотна

У свій час був проведений експеримент, який мав підтвердити корпускулярну природу світла, тобто проявлення корпускулярних власти- востей світла при його взаємодії з речовиною. Прикладом такого розсіювання світла на електронах атомів є синє небо. Електрони атомів у верхніх шарах атмосфери коливаються у полі падаючих хвиль з частотою хвилі, випромінюючи вторинні хвилі з тією ж частотою, а вони створюють розсіяне світло. Наведений приклад пояснюються взаємодією світла з речовиною, і підпадає під корпускулярну теорію. Відповідно до корпускулярної теорії розсіювання світлових променів відбувається трохи інакше.

На електрон налітає фотон, який наділений відповідною енергією і імпульсом. Відбувається зіткнення, яке не можна порівняти із зіткненням більярдних куль.

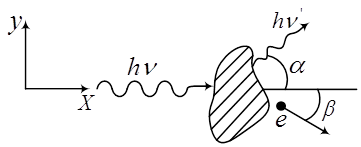
Рис.12

Електрон і фотон якось між собою взаємодіють, а потім розлітаються. Якщо припустити що електрон нерухомий і наділений лише енергію спокою, то після взаємодії з фотоном його енергія зросте, а енергія фотона зменшиться, тобто: . Виходить, розсіяні фотони мають меншу частоту, ніж частота падаючого світла. Подивимося тепер кількісно.

Енергія фотона до зіткнення , а електрона до зіткнення дорівнює енергії спокою . Після зіткнення фотон набуває енергії , а електрон –. Імпульс фотона у проекції на вісь x до зіткнення дорівнює , а після зіткнення . Відповідно у проекції на вісь y імпульс фотона до зіткнення дорівнює 0, а після зіткнення . Закони збереження енергії і імпульсу дають три рівняння:

, (18)

, (19)

. (20)

Ці три рівняння описують зіткнення фотона з електроном. Якщо вважати відомими величинами , а невідомими величини: , а також кути , то маємо п'ять невідомих величин у трьох рівняннях. Це означає, що однозначно описати результат зіткнення фотона і електрона не можна.

Від кута  можна позбутися, якщо рівняння (19) і (20) піднести до квадрату і додати, одержимо

. (21)

Будемо визначати частоту розсіювання  у вигляді функції від кута розсіювання, тобто . Піднесемо рівняння (18) до квадрату і розв’яжемо систему разом з рівнянням (21), тобто

,

.

Знайдемо , врахувавши що  і , одержимо

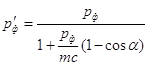. (22)

Вираз (22) дає можливість визначити імпульс розсіяного фотона, вираженого через імпульс падаючого фотона і кут розсіювання .

З формули (22) випливає, що якщо , то , тобто частота розсіяного світла приблизно збігається з частотою падаючого світла. В цьому випадку працює хвильова природа світла. При великих частотах падаючого світла, частота розсіяного світла стає меншою частоти падаючого, а це є гарним підтвердженням корпускулярної природи світла.

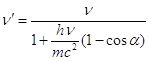Залежність частоти розсіяного світла від частоти падаючого світла легко одержати з формули (22), замінивши  на  і  на , як це показано формулою (23)

(23)

Ефект Комптна є наглядним прикладом підтвердження корпуску- лярних властивостей світла.