Навигация
По формуле (1) можно найти силу, действующую со стороны
11374
знака
0
таблиц
3
изображения
4. По формуле (1) можно найти силу, действующую со стороны
магнитного поля на движущуюся в нем заряженную частицу, только если скорость частицы v перпендикулярна вектору В. В общем случае эта сила равна
(2)
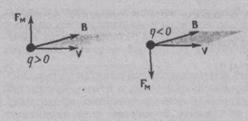На рис. показаны взаимные расположения векторов v, В и FM для положительного и отрицательного зарядов частицы. Модуль силы равен
где 
а — угол между векторами v и В.
Сила FM направлена перпендикулярно скорости v заряженной частицы и
сообщает частице только нормальное ускорение. Иными словами, сила FM не совершает работы и вызывает лишь искривление траектории частицы. Поэтому при движении свободной заряженной частицы в магнитном поле ее кинетическая энергия не изменяется.
5. Если на движущуюся частицу с электрическим зарядом q
одновременно действуют и магнитное, и электрическое поля, то результирующая сила F, называемая силой Лоренца, равна сумме двух составляющих — электрической и магнитной:
(3)
где Е - напряженность электрического поля. Иногда под силой Лоренца понимают только магнитную составляющую силы F.
Разделение силы Лоренца F на электрическую и магнитную
составляющие относительно, т. е. эти составляющие зависят от выбора инерциальной системы отсчета. Дело в том, что при переходе от одной инерциальной системы отсчета к другой изменяются не только скорость v заряженной частицы, но также и силовые характеристики Е и В полей. Соответственно разделение электромагнитного поля на электрическое и магнитное поля тоже относительно.
Эффект Холла.
1. Американский физик Э. Холл провел эксперимент (1879), в котором
пропускал
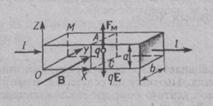постоянный ток I через пластинку М, изготовленную из золота, и измерял разность потенциалов 
между противолежащими точками А и С на верхней и нижней гранях. Эти точки лежат в одном и том же поперечном сечении проводника М. Поэтому,
как и следовало ожидать, оказалось, что 
.
Когда пластина с током была помещена в однородное магнитное поле, перпендикулярное ее боковым граням, то потенциалы точек А и С стали разными. Это явление получило название эффекта Холла. Было установлено, что разность потенциалов между точками А и С пропорциональна силе тока I, индукции В и обратно пропорциональна ширине b пластинки, т. е.
(4)
где R постоянная Холла.
Дальнейшие исследования показали, что эффект Холла наблюдается во
всех проводниках полупроводниках независимо от их материала. Изменение направления тока или вектора В на противоположное вызывает изменение знака разности потенциалов 
Числовое значение постоянной Холла R зависит от материала пластинки М, причем этот коэффициент для одних веществ положителен, а для других отрицателен.
2. Эффект Холла можно объяснить следующим образом. Пусть ток I в
пластинке М обусловлен упорядоченным движением частиц носителей зарядов q. Если их концентрация 
, а средняя скорость их упорядоченного движения v, то сила тока
(5)
где S=ab площадь поперечного сечения пластинки, a vx проекция вектора v на ось ОХ, проведенную в направлении вектора j плотности тока. Если заряд частиц, образующих ток, q> 0, то их скорость v совпадает с направлением тока и vx = v. Если же заряд q<0, то скорость v противоположна по направлению вектору j и vx= — v<0, но qvx =|q|v>0.
На частицу, движущуюся в магнитном поле с индукцией В, действует
магнитная составляющая силы Лоренца FM = q[vB]. При указанных направлениях тока в пластинке М и вектора В сила FM направлена вверх (вдоль положительного направления оси OZ). Под действием силы FM частицы должны отклоняться к верхней грани пластинки, так что на верхней грани будет избыток зарядов того же знака, что и q, а на нижней избыток зарядов противоположного знака. В результате этого в пластинке возникнет поперечное электрическое поле, направленное сверху вниз, если заряды q положительны, и снизу вверх, если они отрицательны. Пусть напряженность образовавшегося кулоновского поля будет Е. Сила qЕ, действующая со стороны поперечного электрического поля на заряд q, направлена в сторону, противоположную силе FM . В случае установившегося состояния сила Лоренца (3), действующая на носитель заряда q, равна нулю:
откуда напряженность установившегося поперечного электрического поля (поля Холла)
(6)
Вектор Е направлен вдоль оси OZ, а его проекция на эту ось равна
(7)
Соответственно разность потенциалов между точками А и С равна
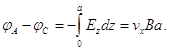
Подставив сюда выражение для vх из (5), окончательно найдем
(8)
Таким образом, полученный результат совпадает с экспериментальной формулой (4).
3. Из сравнения (8) и (5) следует, что постоянная Холла
(9)
Отсюда видно, что знак постоянной Холла совпадает со знаком заряда q частиц, обусловливающих проводимость данного материала. Поэтому на основании измерения постоянной Холла для полупроводника можно судить о природе его проводимости: если R<0, то проводимость электронная, если R>0, то дырочная. Если в полупроводнике одновременно осуществляются оба типа проводимости, то по знаку постоянной Холла можно судить о том, какой из них является преобладающим.
С помощью постоянной Холла можно также определить концентрацию
носителей заряда, если характер проводимости и их заряд известны (например, для металлов):
(10)
Так, для одновалентных металлов оказалось, что концентрация электронов проводимости совпадает с концентрацией атомов.
Зная постоянную Холла для электронного проводника, можно оценить
значение 
средней длины свободного пробега электронов.
где е и т — абсолютное значение заряда электрона и его масса; 
— средняя скорость теплового движения электронов в проводнике; 
— удельная электрическая проводимость. Оказалось, что средняя длина свободного пробега электронов в металлах достигает сотен межузельных расстояний: 
м.
Литература, используемая в реферате:
Детлаф А. А. Курс физики: Учеб. пособие для втузов/ А. А. Детлаф, Б. М. Яворский.- 4-е изд., испр.- М.: Высш. шк., 2002.- 718 с.: ил.
Кикоин А. К. Молекулярная физика: Учеб. пособ. для студентов физ. спец. вузов/ А. К. Кикоин, И. К. Кикоин.- 2-е изд., перераб.- М.: Наука, 1976.- 480 с.: ил.
Иванов Б. Н. Законы физики: Учеб. пособ. для подгот. отделений вузов/ Б. Н. Иванов.- М.: Высш. шк., 1986.- 335 с.: ил.
Савельев И. В. Курс физики: Учеб. пособ. для вузов/ И. В. Савельев.- М.: Наука, 1986.- Т.2.
Похожие работы
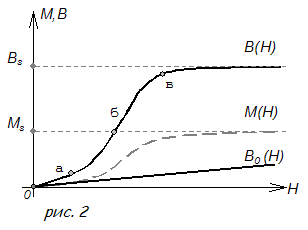
... включать режим I при входном напряжении частотой 50 Гц, т.е. в "сеть" ибо это действие может привести к порче оборудования. При исследовании явления магнитного гистерезиса производится расчеты напряженности магнитного поля и магнитной индукции по выше рассмотренным формулам. Исследование ферромагнитных свойств электротехнической стали. В качестве исследуемого образца был взят ...
... . Опираясь на измерение силы, действующей со стороны магнитного поля на участок проводника с током, можно определить модуль вектора магнитной индукции. 3. Экспериментальное определение индукции магнитного поля и исследование силы Ампера Опытный закон Ампера устанавливает зависимость величины силы, действующей на прямолинейный участок проводника с током, помещенный в магнитное поле, от ...
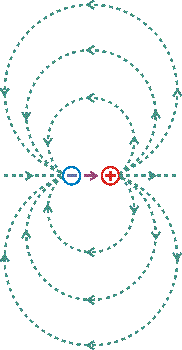
... [N] и [S] - полюса двух электромагнитов, (+) - пробный положительный электрический заряд. Если электромагниты выключать по отдельности, то на заряд будет действовать сила, направленная вверх. «Электромагнитная индукция - возникновение электрического поля, электрического тока или электрической поляризации при изменении во времени магнитного поля или при движении материальных сред в магнитном поле ...
... . Все данные о перечне всех необходимых работ показаны на рис.3.1. Блок-схема разработки реверсной магнитной фокусирующей системы мощного многолучевого клистрона. Получение задания Обзор литературы Изучение и анализ прибора-аналога Расчетно-теоретическая часть ...
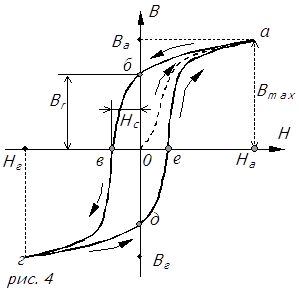
0 комментариев