Навигация
Закон Біо-Савара-Лапласа та його використання у найпростіших випадках
2. Закон Біо-Савара-Лапласа та його використання у найпростіших випадках
Ще на початку 19-го сторіччя французькі фізики Біо і Савар, обробляючи величезний експериментальний матеріал вивчення характеристик магнітного поля провідників зі струмом за участю математика Лапласа, одержали формулу, яка дістала назву у фізиці закону Біо-Савара-Лапласа.
У векторній формі цей закон має вигляд
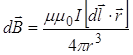 , (11.2.1)
, (11.2.1)
де - відносна магнітна проникність середовища, безрозмірна величина; о – магнітна постійна (![]() ); I – струм у провіднику;
); I – струм у провіднику; ![]() - елемент провідника;
- елемент провідника; ![]() - відстань від елемента струму до точки, в якій знаходиться індукція магнітного поля
- відстань від елемента струму до точки, в якій знаходиться індукція магнітного поля ![]() (рис.11.3).
(рис.11.3).
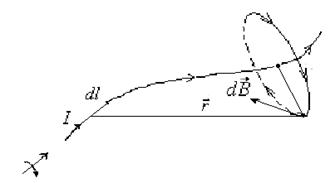
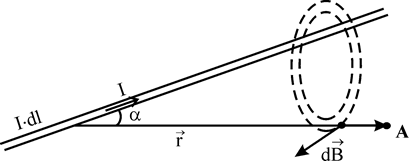
Рис.11.3
З видно, що вектор індукції магнітного поля ![]() є дотичною до силової лінії магнітного поля, яка охоплює провідник, і проходить через точку, в якій визначається індукція магнітного поля.
є дотичною до силової лінії магнітного поля, яка охоплює провідник, і проходить через точку, в якій визначається індукція магнітного поля.
Напрям силової лінії визначається за допомогою правила правого гвинта, як це показано на рисунку.
Поряд із індукцією магнітного поля ![]() магнітне поле характеризується напруженістю
магнітне поле характеризується напруженістю ![]() . Ця величина не залежить від властивостей середовища і дорівнює
. Ця величина не залежить від властивостей середовища і дорівнює
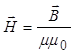 . (11.2.2)
. (11.2.2)
Величина напруженості магнітного поля входить в одне із рівнянь Максвелла. Розмірність напруженості ![]() буде встановлена трохи пізніше.
буде встановлена трохи пізніше.
Закон Біо – Савара - Лапласа для напруженості магнітного поля Н має вигляд
 , (11.2.3)
, (11.2.3)
або в скалярній формі
 .
(11.2.4)
.
(11.2.4)
Магнітному полю властивий принцип суперпозиції. Це означає, що поля від кількох джерел магнітного поля накладаються як вектори, тобто
![]() .
(11.2.5)
.
(11.2.5)
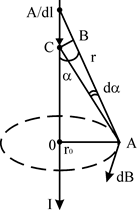
Знайдемо індукцію магнітного поля біля безмежного прямого провідника із струмом (рис.11.4).
Скористаємось законом Біо – Савара - Лапласа в скалярній формі
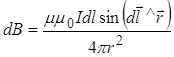 , (11.2.6)
, (11.2.6)
де кут - це кут між напрямком елемента провідника із струмом ![]() і радіусом-вектором
і радіусом-вектором ![]() , як це показано на рис.11.4;
, як це показано на рис.11.4; ![]() - дотичний вектор до силової лінії, напрям якого збігаються з напрямком обертання правого гвинта.
- дотичний вектор до силової лінії, напрям якого збігаються з напрямком обертання правого гвинта.
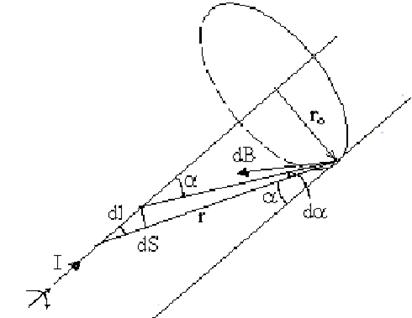
Рис.11.4
З рисунка видно, що
dS=dlsin і dS=rd,
звідки
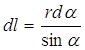 .
.
Радіус-вектор ![]() також можна виразити через ro і кут , тобто
також можна виразити через ro і кут , тобто
![]() .
.
З урахуванням цих зауважень закон Біо – Савара - Лапласа набуде вигляду
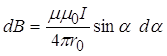 . (11.2.7)
. (11.2.7)
Інтегруємо вираз (11.2.7) в межах зміни кута від 1 до 2, в результаті чого одержимо
 . (11.2.8)
. (11.2.8)
Якщо у виразі (11.2.8) 1 прямує до0, а 2 прямує до , то одержимо безмежний прямий провідник із струмом.
У цьому випадку:
а) індукція магнітного поля буде дорівнювати
![]() . (11.2.9)
. (11.2.9)
б) напруженість магнітного поля буде дорівнювати
![]() . (11.2.10)
. (11.2.10)
З останньої формули легко встановити розмірність напруженості магнітного поля
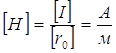 .
.
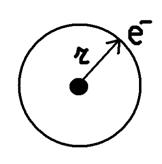
Знайдемо магнітне поле на осі кругового витка із струмом (рис.11.5).
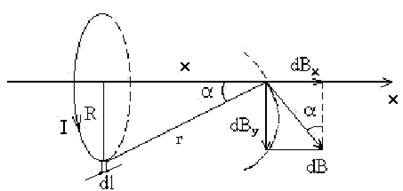
Рис.11.5
Елемент провідника із струмом dl, створює на осі x індукцію магнітного поля dB. Вектор ![]() є дотичним до силової лінії, зображеної на рисунку пунктирною лінією. Складова вектора індукції магнітного поля dBy буде скомпенсована аналогічним елементом з протилежної сторони. Результуючу індукцію магнітного поля від кругового витка із струмом слід шукати в напрямку осі x (принцип суперпозиції магнітних полів).
є дотичним до силової лінії, зображеної на рисунку пунктирною лінією. Складова вектора індукції магнітного поля dBy буде скомпенсована аналогічним елементом з протилежної сторони. Результуючу індукцію магнітного поля від кругового витка із струмом слід шукати в напрямку осі x (принцип суперпозиції магнітних полів).
З рисунка видно, що
![]() . (11.2.11)
. (11.2.11)
Закон Біо – Савара - Лапласа запишеться
![]() , (11.2.12)
, (11.2.12)
тут враховано, що ![]() .
.
Підставимо вираз (11.2.12) у (11.2.11), одержимо
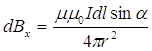 . (11.2.13)
. (11.2.13)
Але врахувавши, що
![]() ; і
; і ![]() ,
,
одержимо
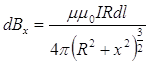 . (11.2.14)
. (11.2.14)
Інтегруємо цей вираз в межах довжини витка від 0 до 2πR, одержимо
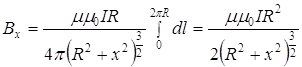 .
.
Таким чином, магнітна індукція на осі кругового витка дорівнює визначається за допомогою формули
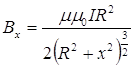 . (11.2.15)
. (11.2.15)
Напруженість магнітного поля у цьому випадку буде дорівнювати
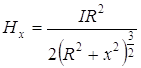 .
(11.2.16)
.
(11.2.16)
Для індукції та напруженості магнітного поля у центрі колового витка зі струмом одержимо
![]() , (11.2.17)
, (11.2.17)
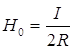 . (11.2.18)
. (11.2.18)
Знайдемо індукцію і напруженість магнітного поля на осі довгого соленоїда з струмом (рис.11.6).

Рис.11.6
Виділений елемент соленоїда шириною dx, в якому dN витків, що щільно прилягають один до одного, можна розглянути як круговий виток, індукція якого розраховується за формулою (11.2.15)
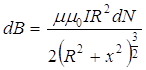 , (11.2.19)
, (11.2.19)
Кількість витків у виділеному елементі соленоїда дорівнює
dN = ndx,
де n – число витків на одиницю довжини соленоїда.
З урахуванням цих позначень одержуємо
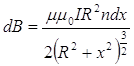 .
(11.2.20)
.
(11.2.20)
Виконаємо заміну змінних у співвідношенні (11.2.20), тобто
![]() , і
, і ![]() .
.
З урахуванням цих позначень одержимо, що
 .
.
Інтегруємо цей вираз у межах зміни кута від 1 до 2. Після інтегрування одержимо
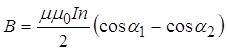 . (11.2.21)
. (11.2.21)
Якщо 10, а 2, одержимо соленоїд безмежної довжини. У цьому випадку:
а) індукція магнітного поля на осі довгого соленоїда
![]() . (11.2.22)
. (11.2.22)
б) напруженість магнітного поля на осі довгого соленоїда
![]() . (11.2.23)
. (11.2.23)
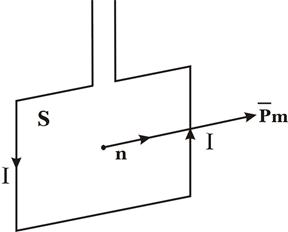
3. Магнітний момент контуру із струмом
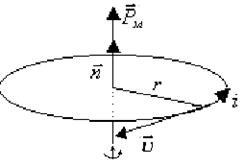
Для плоского контуру із струмом I магнітний момент визначається співвідношенням:
![]() , (11.3.1)
, (11.3.1)
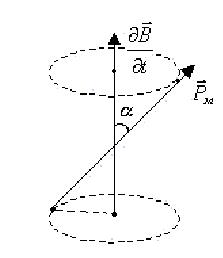
де I – струм у контурі; S – площа контуру; ![]() - нормаль до площини контуру, яка збігається з поступальним рухом правого гвинта, якщо його обертати за напрямком струму у витку.
- нормаль до площини контуру, яка збігається з поступальним рухом правого гвинта, якщо його обертати за напрямком струму у витку.

Рис.11.7
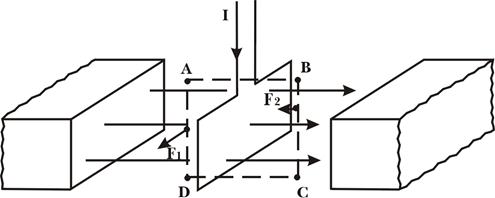
Якщо контур із струмом розмістити у зовнішнє магнітне поле, то результуюча сила Ампера, яка діє зі сторони зовнішнього магнітного поля на контур з струмом, буде дорівнювати нулю, тобто
![]() .
.
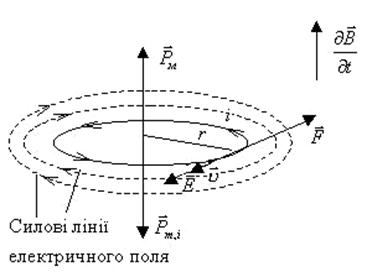
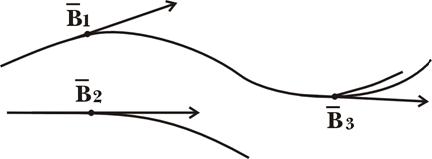
У випадку неоднорідного магнітного поля результуючий вектор сили Ампера не буде дорівнювати нулю.
Відповідні розрахунки показують, що в цьому випадку
![]() (11.3.2)
(11.3.2)
де ![]() - похідна вектора
- похідна вектора ![]() в напрямку нормалі або градієнт вектора
в напрямку нормалі або градієнт вектора ![]() в напрямку нормалі до контуру;
в напрямку нормалі до контуру; ![]() - магнітний момент контуру.
- магнітний момент контуру.
Похожие работы
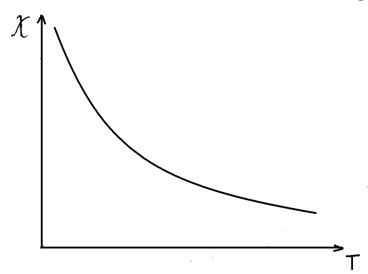
... ; - магнітна сприйнятливість. Із співвідношення (14.2.3) одержуємо: > 1- парамагнетики; < 1 - діамагнетики. Прикладом діамагнітних речовин є металевий вісмут. При внесенні шматочка вісмуту, підвішеного до нитки у зовнішнє магнітне поле, останнє цей шматочок виштовхує з магнітного поля. Парамагнітна мідь або латунь слабо втягуються у зовнішнє магнітне поле. 3. ...
... тного поля в точці на осі колового провідника радіусом R на відстані d від центра колового провідника дорівнює: . Аналогічно обчислюється індукція магнітного поля, створена іншими провідниками з струмом. 2. ЗАКОН ПОВНОГО СТРУМУ ТА ЙОГО ВИКОРИСТАННЯ ДЛЯ РОЗРАХУНКУ МАГНІТНИХ ПОЛІВ. ВИХРОВИЙ ХАРАКТЕР МАГНІТНОГО ПОЛЯ У електростатиці було встановлено, що робота при переміщенні одиничного ...
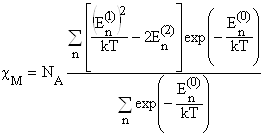
... вираз для макроскопічної магнітної сприйнятливості з урахуванням больцманівського розподілу ансамблю магнітних моментів по енергетичних рівнях приймає вигляд: Це і є рівняння Ван-Флека – основне в магнетохімії, пов’язуюче магнітні властивості з будовою молекул. Тут NA – число Авогадро, k – постійна Больцмана. З деякими крайніми випадками його ми вже зустрічалися вище. Якщо Е(0) = 0, а Е(2) ...
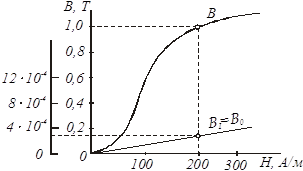
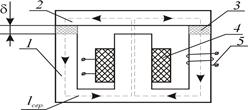
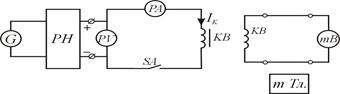
... І = const при вимірюванні. 5.3 Програма роботи 1. Вивчити будову та принципи дії мілівеберметра і мілітесламетра. 2. Вивчити лабораторну установку дослідження характеристик Ш-подібного електромагніта. 3. Експериментальним шляхом зняти вебер-амперну характеристику електромагніта . На підставі експериментальних даних провести необхідні розрахунки і побудувати криву намагнічування B = f(H) і ...
0 комментариев