Навигация
Возникновение и развитие логики
2. Возникновение и развитие логики
Ключевые слова: дедукция, формальная логика, индуктивная логика, математическая логика, диалектическая логика.
Причины и условия зарождения логики. Важнейшей причиной зарождения логики является высокое развитие интеллектуальной культуры уже в древнем мире. Общество на той стадии развития не удовлетворяется существующим мифологическим истолкованием реальности, стремится рационально интерпретировать суть явлений природы. Постепенно складывается система умозрительного, но вместе с тем доказательного и последовательного знания.
Особая роль в процессе становления логического мышления и его теоретического изложения принадлежит научному знанию, которое к тому времени достигает значительных высот. В частности, успехи в математике, астрономии приводят ученых к мысли о необходимости изучения природы самого мышления, установления закономерностей его протекания.
Важнейшими факторами становления логики была потребность в распространении в социальной практике активных и убеждающих средств выражения взглядов в политической сфере, судебном деле, торговых отношениях, воспитании, обучающей деятельности и пр.
Основоположником логики как науки, создателем формальной логики принято считать древнегреческого философа, античного ученого энциклопедического ума Аристотеля (384 – 322 гг. до н.э.). В книгах «Органона»: «Топика», «Аналитики», в «Герменевтике» и др. мыслитель разрабатывает важнейшие категории и законы мышления, создает теорию доказательства, формулирует систему дедуктивных умозаключений. Дедукция (лат.: выведение) позволяет выводить истинное знание о единичных явлениях, исходя из общих закономерностей. Аристотель впервые подвергает исследованию само мышление как активную субстанцию, форму познания и описывает условия, при которых оно адекватно отражает действительность. Логическую систему Аристотеля часто называют традиционной, поскольку в ней содержатся основные теоретические положения о формах, и приемах мыслительной деятельности. Учение Аристотеля включает в себя все основные разделы логики: понятие, суждение, умозаключение, законы логики, доказательство и опровержение. По глубине изложения и общезначимости проблематики его логику называют классической: пройдя испытания на истинность, она и сегодня сохраняет свою актуальность, оказывает мощное воздействие на научную традицию.
Развитие логического знания. Дальнейшим развитием античной логики стало учение философов-стоиков, которые вместе с философско-этической проблематикой логику считают «проистечением мирового логоса», его земной, человеческой формой. Стоики Зенон (333 – 262 гг. до н.э.), Хрисипп (ок.281 – 205 до н.э.) и др. дополняют логику системой высказываний (пропозиций) и выводов из них предложили схемы умозаключений на основе сложных суждений, обогатили категориальный аппарат и язык науки. К этому времени (3 в. До н.э.) относится возникновение самого термина «логика». Логическое знание преподносилось стоиками несколько шире классического воплощения. Оно соединило в себе учение о формах и операциях мышления, искусство ведения дискуссии (диалектика), мастерство публичных выступлений (риторика) и учение о языке.
В Новое время в период широкого распространения в Европе естественнонаучного знания (механика, география и т. Д.) возникают потребности в дополнении системы дедуктивных умозаключений принципами индуктивного мышления. Накопленный эмпирический, фактический материал, частные случаи из практики и жизни путем сравнений и обобщений оказалось возможным построить так, что они приведут к истинным суждениям общего характера. Знание о единичных вещах может «навести» (лат.: inductio) на мысль о наличии общих закономерностей их существования. Это свойство мышления как научную закономерность в противоположность схоластическим рассуждениям отметил в своем труде «Новый Органон или Истинные указания для истолкования природы» английский философ и естествоиспытатель Фрэнсис Бэкон (1561 – 1626). Он выступил, таким образом, родоначальником индуктивной логики
Специфику научного познания отразил в рационалистической методологии французский мыслитель Нового времени Рене Декарт (1596 – 1650). В «Рассуждении о методе, чтобы верно направлять свой разум и отыскивать истину в науках» и «Правилах для руководства ума» он формулирует важнейшие методы познания: аксиоматический, аналитический и синтетический, а также, в завершении познания, метод систематический. Высшей формой реализации рационалистической методологии, по Декарту, является математика. Логике отводится роль методологии познания, способной обнаружить пути обретения новых истин, приращения знания.
Основополагающие идеи математической (или символической) логики были предложены немецким мыслителем Г.В.Лейбницем (1646 – 1716) в работах «Об искусстве комбинаторики», «Опыт универсального исчисления», «О математическом определении силлогических форм» и др. Он развивает вопросы традиционной логики (формулирует закон достаточного основания, работает над систематизацией категорий логики и пр.), но больше внимания уделяет формализации языка, математизации стиля логического мышления. С этого времени в логике стали использоваться специальные знаки-символы, не употребляющиеся в естественном языке. Лейбниц впервые исследовал возможности арифметизированного логического вывода на основании соответствия законов логики и законов математики. Этим ставится цель привести теоретические научные рассуждения к математическим расчетам, благодаря которым возможно разрешить любой спор и прийти к истине.
На смену традиционной логике приходит математическая, заключающая мыслительные формы в строгие формулировки правил и теорем, реализуемых в аналитических приемах мыслительной деятельности.
В ХIХ в. символическая логика становится наиболее привлекательной сферой логического знания. Среди наиболее известных представителей математической логики выделяется английский математик Д. Буль (1815 – 1864). В работах «Математический анализ логики» и «Исследование законов мышления» он закладывает основы алгебраических исчислений конкретных элементов (классов) как отношений (операций). Буль стремился перевести на язык знаков отношения между идеями, объектами и абстрактными системами. Булева алгебра – это решение логических задач путем использования трех операций: а) сложение классов (А U В), умножение классов (А ∩ В), и дополнение к классу (А′). Алгебра Буля была применима и в прикладных случаях, например, при интерпретациях конкретно-релейных схем, в исчислениях при программировании в ЭВМ и т.д.
Формальная и символическая логика. Формальная (традиционная) логика предметом своего исследования имеет исследование основных форм мышления (понятие, суждение, умозаключение), законов, находящиеся в их сфере, непосредственно не опираясь на конкретное содержание мысли. Формальная логика абстрагируется от исторического процесса, от развития практических и познавательных способов действия.
Символическая (математическая) логика может быть представлена как формальная, как ее формализованная часть. Основной своей задачей она видит построение логических исчислений путем математических формул, аксиом и следствий. Она излагает формы мышления в системе знаков и специальных символов.
Современная формальная логика предусматривает изучение мыслительных операций и перенесение логических форм на общие образцы теоретического знания. Современная символическая логика является самостоятельным направлением логического знания, имеет не только теоретическое, но и практическое значение. Так, помимо сложных вычислительных операций, она широко используется в лингвистике (при переводах с одного языка на другой), технической сфере (при управлении приборами), в компьютерном программировании и пр.
Формальная и диалектическая логика. Формально-логические схемы, так сказать, безразличны (нерелевантные) к сущности познаваемых предметов. Сущность – совокупность внутренних качеств и признаков предмета, выражающих его содержание. Важнейшими способами проникновения в сущность вещей является обнаружение противоречивого единства их признаков, рассмотрение их в развитии и взаимосвязи с другими предметами. В процессе такого познания важно абстрагироваться от несущественного, случайного, концентрируя познания на атрибутивных признаках.
В отличие от формальной, логика диалектическая своим предметом имеет исследование возникновения и развития фрагментов действительности, в том числе и логических форм и законов. Это – познание развивающегося мышления. В основе логики диалектической находится ряд принципов: а) принцип развития, б) принцип историзма, в) принцип всесторонности, г) принцип конкретности и др. Центральным понятием диалектической логики является диалектическое противоречие.
Диалектическая логика, накапливая и обобщая свое знание в течение всего периода развития логики, в систематизированном виде была изложена в немецкой классической философии. В работах И. Канта (1724 – 1804) «Критика чистого разума» и «Критика способности суждения» проведено обоснование трансцендентальной логики, определяющей происхождение, содержание и объективную значимость априорных знаний. В философии Гегеля (1770 – 1831) нашла свое завершение объективно-идеалистическая система диалектической логики как всеобщей формы самопознания и саморазвития понятия. В работе «Наука логики» он не только подвергает критике формально-логические законы мышления как «неонтологические», но и обосновывает принципиально иное содержание логических знания – законов, понятий и умозаключений, в основе которых находится диалектика мышления объективного духа.
Новый этап в понимании диалектической логики связан с именами К. Маркса (1818 – 1883) и Ф. Энгельса (1820 – 1895). В работах Ф. Энгельса «Анти-Дюринг», «Диалектика природы», К. Маркса «Капитал» и др. толкование развивающихся форм основывается не на изначальности «саморазвивающегося понятия», а на обнаружении диалектических изменений в самом объективном (материальном) мире. Природа и общество, с их точки зрения, являются основанием для понимания законов диалектического мышления. В марксистской диалектике с материалистических позиций формулируются три важнейших закона диалектики (закон единства и борьбы противоположностей, закон взаимного превращения количественных и качественных изменений, закон отрицания отрицания), основные принципы и категории материалистической диалектики.
Если формальная логика познает формы мышления посредством анализа важнейших признаков без непосредственной связи с конкретным предметом, в обобщенном и абстрагированном виде, то диалектическая логика акцент изучения сущности мыслимых предметов переносит на анализ предметов и процессов в движении, развитии и взаимосвязи. В этом случае несущественные, случайные признаки отсеиваются, аннулируются, а существенные выделяются, актуализируются.
Тем не менее, нельзя противопоставлять диалектическую и формальную логику. Они изучают один и тот же объект – человеческое мышление, предметом обеих являются закономерности мыслительной деятельности. Мышление подчиняется и формальным логическим законам как фундаментальным, и диалектическим как развивающимся. Мыслить диалектически невозможно без постижения и учета законов формальной логики. Т.е., возможно заключить, что современное логическое знание включает в свою структуру две взаимосвязанные и относительно самостоятельные науки: формальную логику (частью которой является логика символическая) и диалектическую логику. Причем, признавая фундаментальное значение логики в построении всякого правильного мышления, научно-теоретическое познание требует продолжения изучения сущности явлений и структур мысли путем обнаружения противоречий в природе, обществе и в человеческом мышлении.
Задачи и упражнения
1. Пользуясь математической последовательностью действий, раскройте секрет угадывания чисел. Задумайте любое число, отнимите от него 1, результат умножьте на 2, из полученного произведения отнимите задуманное число и сообщите результат. Как отгадать задуманное товарищем число?
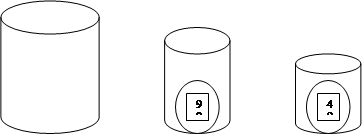
2. Как отмерить 6 литров воды, если имеются ёмкости 9 литров и 4 литра:
3. В античной риторике была разработана схема построения выступления, состоящая их пяти важнейших этапов. Расположите их в логической последовательности:
произношение, словесное оформление, изобретение, план, запоминание.
4. Составьте подробную логическую схему или таблицу, раскрывающую историю развития логического знания.
3. Язык логики
Ключевые слова: язык, семиотика, семантические категории, искусственный язык, термин.
Язык как знаковая система. Предмет логики – законы и формы мышления. Мышление – идеальная реальность. Все, происходящее в сознании человека, не поддается непосредственному опредмечиванию, материализации. Оно не может быть изучено адекватно без подключения специальных средств выражения мысли. Мы часто задаем вопрос: с помощью каких процессов возможно познание мыслительной деятельности человека? Это, в первую очередь, и в конечном итоге – через язык и посредством языка. Мышление человека реализуется в неразрывной связи с языком, речью, передается другим с помощью языковых выражений. Вот почему логика исследует мышление, опираясь на его конкретную фиксацию в языке.
Язык – это (в наиболее общем виде) любая знаковая информационная система, используемая человеком для общения и познания. Язык функционально способен хранить, перерабатывать и транслировать информацию. Кроме этого, язык является необходимым средством отображения человеком объективного мира, его фрагментов, а также субъективной реальности, эмоций, впечатлений и пр., что позволяет человеку адекватно построить процесс их изучения.
В исследовании языковых выражений мысли логика видит свою одну из основных и непосредственных задач. Изучением языка как знаковой системы занимается семиотика, выявляющая специфику его построения и употребления. Один из ее разделов – синтаксис – анализирует специфику, структуру, способы образования и преобразования языка, отношений между знаками системы. Например, отношения равенства (3 + 2 = 5), отношения следования («Cogito ergo sum»), отношения доказательства (доказательство теоремы Пифагора) и пр.
Прагматика как раздел семиотики изучает отношения между знаками системы и их потребителями, практически значимые отношения. Они могут быть вызваны экономическими, эстетическими, духовно-психическими потребностями и т.д. и меньше всего задействованы в логике. Например, построение языковых выражений с наибольшими допустимыми сокращениями либо упрощениями с целью эффективного применения с конкретной речевой ситуации (управление, приказ, телефонный разговор и пр.).
Существует еще один тип отношений, без которого немыслимо ни построение языка, ни его практическая реализация. Это – семантическое отношение: отношение между знаками системы и обозначаемыми ими объектами, предметом и его именем (теория референции), отношение знаков и содержания ими замещаемого, смыслового выражения языка (теория смысла). Этот раздел называется семантикой. Семантические категории обозначают такой класс языковых смыслов и референций, который сохраняет свою осмысленность при замене одного знака другим. Например, высказывание 3 + 2 = 5 остается осмысленным при замене знака «2» на знак «3», или, скажем, если знак «+» заменить на знак «-». Теряя при этом истинность, оно останется семантически определенным. В языке традиционной логики существует три общих класса семантических категорий: имя, функтор, высказывание.
Естественный и искусственный языки. Логика не только изучает, но и использует языковую знаковую систему. В обществе язык существует в двух формах. Это, во-первых, естественный язык как исторически и национально сложившиеся звуковые (речь) и графические (письмо) знаки-сигналы, позволяющие удовлетворить потребности в получении, накоплении, передаче и хранении информации. Наиболее распространенной разновидностью естественного языка является национальный (народный) язык. Второй формой языка выступает искусственный язык. Под ним понимается определенная знаковая система, специально созданная для обслуживания и удобного использования и передачи научной и другой информации. Среди искусственных языков - формализованные языки математики, физики, химии, языки программирования для ЭВМ и т.д., располагающие своей собственной терминологией и символикой.
Следует помнить, что естественный язык имеет ряд черт, мешающих адекватно, четко и однозначно передать форму мысли (полисемия, аморфность, метаязык и пр.). Поэтому для точного отражения структуры мысли слова обычного языка заменяются специфическими терминами-символами. В логике, таким образом, используется как естественный язык (способ описания логических выражений, теоретического построения логического знания), так и искусственный (совокупность знаков, формул и их сочетаний для обозначения мыслительных операций).
Логические термины и символы. Для описания свойств изучаемых предметов, отношений между ними и установлению логической формы не достаточно использовать только естественный язык. Необходимо разработать специальную терминологию (термин – слово, имеющее строго однозначный смысл), установить метаязыковые взаимодействия, а также придать им единую символику и знаковое соответствие. Например, в языке математики существует 5 основных категорий: число, действие, отношение, скобка левая и скобка правая (как операционные последовательности и завершенности действий). Среди логических терминов выделяют ряд терминов:
Имя – слово или словосочетание, обозначающее какой-либо определенный предмет мысли. Под предметом понимаются различные вещи, процессы, отношения и т.д. Например, человек, гуманизм, деятельность и т.д. Имена разделяются на:
а) простые и сложные (описательные): например, соответственно - земля и столица Республики Беларусь);
б) единичные (собственные) и общие (например, соответственно - Василь Быков и закон).
Множество предметов, к которым относится данное имя, называется денотатом, а совокупность присущих им (предметам) признаков и свойств, составляющих их смысловое значение, называется смыслом (концептом).
Высказывание – языковое выражение, содержащее истинную либо ложную мысль. Например, «Наполеон был императором Франции». Это – грамматически правильное, семантически определенное, четко сформулированное, завершенное повествовательное предложение. Например, «Простые числа делятся на два типа». Высказывание бывает истинным либо ложным. Это его логические значения. Например, высказывание «Солнце размерами больше Марса» является истинным, однако перестановка местами имен в этом высказывании приведет к ложному значению.
Выражение, служащее в высказывании средством образования новых осмысленных высказываний, называется функтором. Функтор не является ни именем, ни высказыванием. Это – служебное языковое образование, посредством которого так называемые аргументы образуют новое высказывание. Например, Если а = в, то 2а = 2в, 2 + 3 = 5. В этих примерах функторами выступают знаки математических связей: «=» и «+». Функторы бывают одноаргументными (Лес зазеленел), двухаргументными («Подлость опаснее лжи», 3 + 4 и т.д.). В традиционной логике двухаргументные функторы часто называют логическими союзами (логическими связками).
В науке широко используется понятие функции как соответствия между переменными величинами х и у. В математике она записывается в виде выражения у = f(x). В логике также это понятие существует, большую значимость имеют понятия именной и пропозициональной функции.
Именная функция – выражение, которое содержит переменные, превращающиеся в имя при подстановке вместо них соответствующих аргументов. Примерами именной функции могут быть выражения «космонавт х», «брат у». То есть, при замене переменных х и у данные выражения превращаются в обозначение предмета, название, именование вещи и пр.
Пропозициональная функция выражает собой форму высказывания, в которой при подстановке вместо переменных соответствующих значений образуется семантически определенное высказывание. Например, х больше у, х открыл закон прибавочной стоимости. Пропозициональная функция, аргументы которой – имена, называется предикатом. Например, R является президентом фирмы. Предикат, обозначающий свойство предмета и имеющий одну переменную – имя, называется одноместным предикатом (А обозначает качество). Двух (n - местные) предикаты, располагая двумя и более количеством переменных обозначают отношения между именами – переменными: «а любит в», «а находится между в и с» и пр.
В логике существует потребность выражать различные степени связывания переменных посредством так называемых операторов. Наиболее распространенными операторами являются а) квантор общности, констатирующий наличие свойства, качества, отношения, присущие всему классу явлений по принципу «для всякого х истинно, что…». К примеру, такой квантор содержит высказывание «Всякий предмет тебе разъяснят философские книги» (Гораций). б) квантор существования, обозначающий распространенность тех или иных свойств или отношений на некоторую часть из всего класса явлений. Например, фраза «Существует внутреннее мужество – мужество совести» (С. Смайлс) содержит квантор существования. Формулой квантора существования является выражение: «существует х, для которого…».
Обобщая общепринятую и чаще всего используемую логическую терминологию, следует ее запечатлеть в формализованном виде:
1) имя - А, В, С и т.д.;
2) функторы (логические константы) –
Ù - «и»;
Ú - «или»;
® - «если, то»;
« - «тогда и только тогда, когда»;
ù , ¯¯¯ - «неверно, что»;
![]() - «необходимо» ;
- «необходимо» ;
à - «возможно»,
3) предметные переменные – а, в, с;
4) пропозициональные переменные – p, q, r, s;
5) именная функция - а (х);
6) пропозициональная функция - х Р(х);
7) предикатор - P, Q, R; одноместный предикат - Р (х): (х имеет свойство Р); двухместный предикат Р (х; у): (х и у имеют отношение к Р);
8) скобки - ( ; );
9) квантор общности - " х (для всякого х верно, что…);
10) квантор существования - $ х (существует х, для которого верно, что…).
Таким образом, понимая познавательную ценность языка, его связь с мыслительными процессами, необходимо усвоить логическую терминологию и суть основных знаков, используемых в логических формулах.
Задачи и упражнения
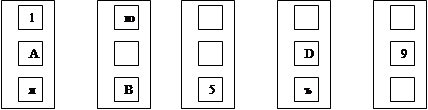
1. Вставьте пропущенные цифры и буквы в пустые квадраты, используя скрытые последовательности цифр и букв.
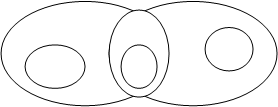
2. Расставьте в круговой схеме заглавные буквы соответствующих видов языков, определяя тем самым их соотношение: Е – естественный язык, Н – научный язык, И - искусственный язык:
3. Составьте языковые выражения, отражающие:
а) отношение доказательства; б) отношение следования, в) осмысленное, но ложное высказывание; г) именную функцию; д) квантификацию существования.
4. Проведите сравнительную характеристику формализованного и естественного языков логики.
5. Преобразуйте пропозициональные и именные функции в истинные высказывания: а) х причина у; б) х – простое число; в) А – город в Беларуси; г) Х – автор романа «У»; д) между а и в расположено с; е) если р то q.
4. Формы и законы мышления
Ключевые слова: форма мысли, логический закон, логическое следование.
Основные формы логического мышления. Логической формой мысли называется строение этой мысли с точки зрения способа соединения ее составных частей, образования общих структурных связей (схемы изложения мыслей). Выявить логическую форму значит построить ее схему, формализовать ее содержание, поскольку логической формой является та сторона рассуждения, которая не зависит от содержания данной мысли. Различные понятия, суждения и умозаключения можно представить как специфические формы мыслительной деятельности. На основании одного из основных принципов формальной логики правильность мысли (рассуждения, вывода) зависит только от правильности ее оформления, т.е. от правильного соединения, связывания составных частей мысли.
Выделяя характерные признаки предмета, а также на основании общих признаков, присущих многим предметам, в мышлении тем самым образуется понятие о предмете, о его классификационных, существенных признаках, одновременно, отличающих его от признаков предметов другого класса. Таким образом, различная связь четко обозначенных, перечисленных признаков предмета (класса предметов) выражается в форме понятия. Понятие квадрата, например, включает в себя следующие признаки: геометрическая фигура, четырёхугольник, все стороны равны, все углы имеют 90 градусов.
Форма мышления, устанавливающая качественные и количественные отношения между предметами мысли и фиксирующая их в виде утверждений либо отрицаний называется суждением. Так, например, отношение человека к благам посредством производственной деятельности может быть выражено в суждении «Человек в процессе трудовой деятельности создает материальные и духовные блага». Суждения, различные по содержанию, по эмоционально-оценочным и прочим аспектам, всегда можно свести к единой унифицированной форме (структуре) мысли. Способ соединения всех его частей с точки зрения формальной логики будет одинаков. Если мы обозначим понятия, входящие в структуру суждения, знаками S (субъект мысли), т. е. то, о чем (о ком) идет рассуждение) и Р (предикат – констатация, выражение признаков либо свойств обозначенного субъекта (S)). Если способ их связи мы представим в виде логической связки «есть» (является, значит и т. п.), то получим логическую форму, общую для любых суждений: S - Р (Все S суть Р). К примеру, структура высказываний: «Всякий человек достоин счастья», «Река – водная артерия земли» и «Сумма углов треугольника равняется 180 градусам» в принципе одинакова, несмотря на их содержательную, смысловую полифонию. В них можно выделить S (человек, река, сумма углов треугольника), Р (достоин счастья, водная артерия земли, 180 градусов) и утвердительную логическую связку, в данных примерах подразумевающуюся, но лингвистически невыраженную.
Более сложной формой мышления, приводящей к установлению нового знания, благодаря тому или иному способу соединения предыдущих суждений-оснований, выступает умозаключение. В этом случае устанавливается четкая однозначная логическая связь между суждениями-основаниями (посылками), соблюдение которой приводит всегда к новому истинному выводу-следствию. Например, какое знание можно получить, располагая двумя суждениями (предложениями): «Всякое научное знание имеет свой предмет изучения» и «Культурология является научным знанием»? Заключение (вывод) здесь очевидно – «Культурология имеет свой предмет изучения». Какие бы высказывания не подставлялись в структуру такого правильного рассуждения, если посылки истинны, соблюдены правила вывода, значит и заключение (новое знание) также будет истинным.
Таким образом, логическая форма, во-первых, - это своеобразная языковая структура, в чистом виде отражающая присущие предмету мысли признаки, свойства и отношения.
Во-вторых, для ее фиксации используется специфический формализованный язык, основные термины и символы которого были представлены выше.
В-третьих, изучение этих и иных структур мысли (логических форм) безотносительно к их содержательному выражению составляет одну из важнейших задач логики как науки и позволяет устанавливать законы образования и протекания мыслительных процессов.
Логический закон и логическое следование. С понятием логической формы связаны понятия логического закона и логического следствия. Правильная связь элементов мыслей в ходе рассуждения определяется законами мышления – логическими законами. Логическим законом называется выражение, сохраняющее свою истинность, независимо от его конкретного содержания. Так, высказывание «Если для всех х верно, что х есть Р, то ни существует ни одного х не являющегося Р» будет истинным (являться законом) в любом случае, какое бы конкретное содержание оно не имело. Например, подставив в эту языковую формулу имена, получим: «Если для всех людей верно, что они обладают сознанием, то не существует ни одного человека, у которого оно отсутствует».
Закон выражает внутреннюю, устойчивую, существенную и необходимую связь элементов мышления. Благодаря наличию законов логики выведение нового знания из уже имеющихся и проверенных, истинных суждений с достоверностью приведет к истине.
Законы логики следует разделять на 1) формально-логические и 2) диалектические. Первые отражают формальную правильность рассуждений, вторые – закономерности объективно изменяющейся реальности. Формально-логические законы утверждают, что правильно построенная схема мыслей является необходимым условием для истинности выводов. В противном случае, если не соблюдается это правило, то ложный вывод (неистинное следствие) возможен даже из истинных суждений.
Основными формально-логическими законами считаются:
1. закон тождества: всякая мысль в процессе рассуждения должна быть тождественна самой себе. ((р → р): если р, то р). «Всякий человек – это человек», «Dura lex, sed lex» (суров закон, но закон).
2. закон непротиворечия: из двух несовместимых друг с другом суждений одно является ложным.ù(р Ù ùр): ( неверно, что р и не-р). Т. е. не может быть одновременно ложными две мысли, если одна из них отрицает другую. Причем, речь идет об одном и том же предмете мыслимом в одно и то же время и в конкретном отношении. « Некоторые ученые хотят быть признанными» и «Некоторые ученые не хотят быть признанными».
3. закон исключенного третьего: истинно либо само высказывание, либо его отрицание: (р Ú ùр): (р или не-р). «Некоторые студенты первого курса связаны с экономической деятельностью. Ни один студент первого курса не связан с экономической деятельностью». Т. е. одновременно истинным не могут быть два противоречивых высказывания, одно из них обязательно ложно. Третьего варианта не дано. Снег бел, либо не бел.
4. закон достаточного основания: мысль является истинной, если она имеет достаточное для этого основание. (р → q); (р есть потому, что есть q). Доказанность мысли наступает лишь тогда, когда она опирается на обоснованные, существенные, основополагающие аргументы. Вот один из примеров: «Для того чтобы треугольник был равносторонним необходимо и достаточно, чтобы все его углы были равны».
Законы мышления – это проявление так называемого логического следования. Логическим следованием называется мыслительное отношение, которое существует между посылками (суждениями) и выводимыми из них заключениями (выводами). Логическое следование выступает своеобразной моделью построения мысли по принципу: когда из нашего высказывания р логически следует высказывание q и это высказывание истинно как р → q, то на этом основании новое высказывание ùq → ùp также будет истинным. То есть, истинность высказывания р → q, гарантирует истинность высказывания ùq → ùр . Основным принципом логического следования является утверждение о том, что правильность более общей схемы гарантирует правильность менее общей схемы, но не наоборот.
Задачи и упражнения
1. Приведите примеры основных логических форм мышления из выбранной вами профессиональной деятельности:
а) понятие; б) суждение; в) умозаключение.
2. Являются ли следующие высказывания проявлением законов логики:
а) достаточного основания: «У человека повышена температура тела, следовательно, он заболел», «Данная мысль построена правильно, поэтому она истинна»;
б) исключенного третьего: «Все студенты изучают логику или ни один из студентов не изучает логику», «Постановление суда является законным или не является таковым»?
Похожие работы
... в лице читателя или слушателя, а это возможно только тогда, когда речь логически организована. 4. Основные формально-логические законы 4.1 Общие замечания Хорошо известно, что логика как наука имеет длительную и богатую историю. В лице логики человечество вырабатывало науку о мышлении из поколения в поколение, и на этом пути оно достигло высоких результатов. Как и каждая зрелая наука ...
... логики и уделили главное внимание методологии научного познания, логике открытий. Логика рассматривалась ими как познавательное орудие всех наук. Создание подобных «расширенных логик» стало характерным в XIX—XX вв. 2. Основные исторические этапы развития логики 2.1 Становление символической (математической) логики Подлинную революцию в логических исследованиях вызвало создание во второй ...
... , она должна оперировать понятиями «истинность мышления» и «правильность рассуждения». «Правильное мышление» основано на логике. Именно логика, умело подобранная в соответствии с предметом рассмотрения, делает мысли адекватными реальности. Обычно истинность мышления определяют как соответствие знания объекту. Истина – это адекватная информация об объекте, получаемая посредством его чувственного ...
... структур, а, следовательно, и структур мышления. Итак, формальная логика есть наука об общих структурах правильного мышления, о законах и формах выводного знания, т.е. знания, полученного из ранее установленных и проверенных истин. Это и есть предмет формальной логики как науки. Методологическое значение формальной логики сводится, таким образом, к следующему: - формальная логика является " ...

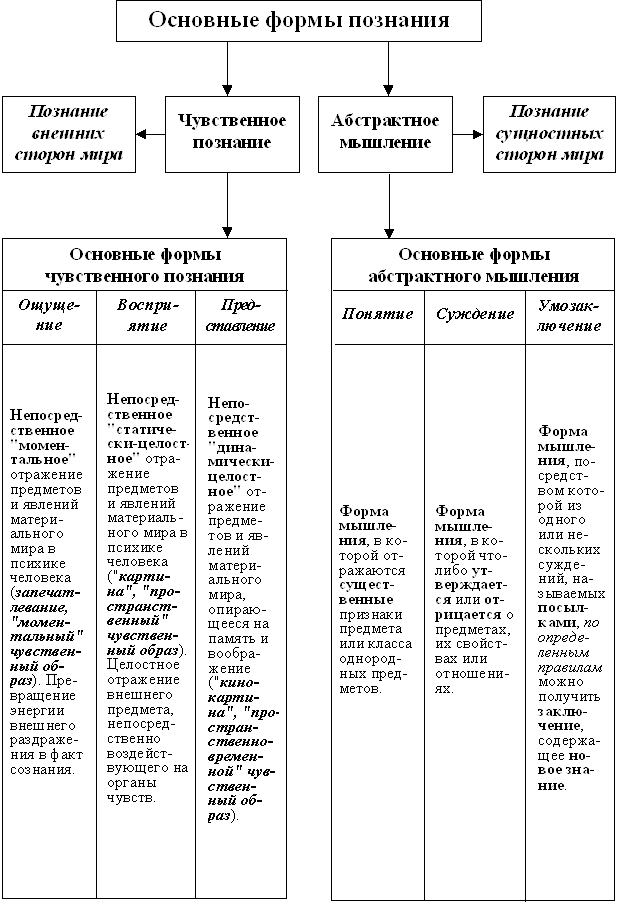



0 комментариев